仧奀奜偺戝妛惗丂Hirasawa Yasutaka偝傫偐傜偺夝摎丅
丂丂丂丂丂乮University of North Carolina at Chapel Hill乯
X = 80 degree (I hope it is right???):
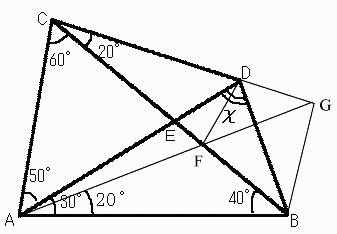
Draw a line L1 from point A so that L1 has an angle of 20 degree to AB, 60 degree to AC.
Call an intercept of L1 and CB as F.
Call an intercept of L1 and extended CD as G.
It is easy to show that triangle ACF and FGB are equilateral triangles.
(ACF is clear. For FGB, use congruence of triangles ACG and CAB. and so on)
Now, triangle ACD is an isosceles triangle, thus AC = CD.
Since AC = CF (ACF is equilateral),CDF is an isosceles triangle.
Using this fact, we can get angle DFC = 80.
This implies that angle DFG is 40.
Also it is easy to see that angle DGF is 40.
These implies triangle DGF is isosceles and DF = DG.
Therefore triangles DBF and DBG are congruent.
Thus, angles FDB and BDG are equal to 50.
It must have been clear that Angle CDA is 50 and CDF is 80 by now.
This implies EDF is 30.
Finally X is equal to EDF plus FDB, or 80 degree.
I haven't enjoyed this kind of problems for 25 years...Took some time to adjust my thinking mode.
Thanks. I could enjoy going back to CHUUGAKUSEI KIBUN for about 40 min...
亂僐儊儞僩亃
丂傒偛偲俉侽並偱惓夝偱偡丅
偙偺傗傗偙偟偄栤戣傪妝偟傫偱偄偨偩偄偰偳偆傕偁傝偑偲偆偛偞偄傑偟偨丅
偝偭偦偔栤戣傪弌戣偟偨惗搆偵抦傜偣偨偄偲巚偄傑偡丅
傢偐傝傗偡偄愢柧丄偳偆傕偁傝偑偲偆偛偞偄傑偟偨丅
亙惵栘栿亜怣梡偟側偄偱偔偩偝偄偹丅(^_^;
佢倃偼俉侽搙乮惓夝偩偲偄偄側偀乯
揰俙偐傜丄俙俛偵懳偡傞妏搙俀侽搙丄俙俠偵懳偡傞妏搙俇侽搙偱捈慄俴侾傪傂偔丅
俴侾偲俠俛偲偺岎揰傪俥偲偡傞丅
俴侾偲俠俢偺墑挿偲偺岎揰傪俧偲偡傞丅
仮俙俠俥偲仮俥俧俛偑惓嶰妏宍偱偁傞偙偲傪帵偡偺偼傗偝偟偄丅
乮仮俙俠俥偼柧傜偐丄仮俥俧俛偵偼仮俙俠俧偲俙俠俛偺崌摨側偳傪巊偆丅乯
偝偰丄仮俙俠俢偼擇摍曈嶰妏宍偱偁傞丅
偟偨偑偭偰俙俠亖俠俢丅
俙俠亖俠俥乮仮俙俠俥偼惓嶰妏宍乯偩偐傜仮俠俢俥偼擇摍曈嶰妏宍丅
偙偺偙偲傪巊偆偲丄佢俢俥俠亖俉侽搙偲傢偐傞丅
偙偺偙偲偵傛傝佢俢俥俧偼係侽搙丅
傑偨佢俢俧俥傕娙扨偵係侽搙偲傢偐傞丅
偙傟傜偺偙偲偐傜仮俢俧俥偼俢俥亖俢俧偺擇摍曈嶰妏宍偱偁傞丅
備偊偵仮俢俛俥偲仮俢俛俧偼崌摨偱偁傞丅
偟偨偑偭偰佢俥俢俛偲佢俛俢俧偼俆侽搙偱偁傞丅
佢俠俢俙偑俆侽搙偱佢俠俢俥偑俉侽搙偱偁傞偺偼丄偡偱偵柧傜偐偱偁傞丅
偟偨偑偭偰佢俤俢俥偼俁侽搙丅
嵟屻偵倃偼佢俤俢俥亄佢俥俢俛偵摍偟偄偺偱俉侽搙丅

俀俆擭傎偳偙偺傛偆側栤戣傪妝偟傫偩偙偲偑側偐偭偨偺偱丄峫偊曽傪偁傢偣傞偺偵偟偽傜偔帪娫偑偐偐傝傑偟偨丅
偁傝偑偲偆丅
係侽暘娫傎偳丄拞妛惗婥暘偵傕偳偭偰妝偟傓偙偲偑偱偒傑偟偨丅
仧惵怷導丂takerun 偝傫偐傜偺夝摎丅
仮ACD偼擇摍曈嶰妏宍丅乮佹佢CDA=50搙乯
乮AC=CD乧(1)乯
崱丄AB忋偵揰F傪佢CFA=80搙偲側傞傛偆偵偲傞偲丄仮ACF偼擇摍曈嶰妏宍丅
乮AC=CF乧(2)乯
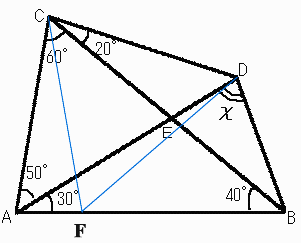
傑偨丄佢ACF=20搙偱偁傞偐傜佢FCE=40搙丅乧(3)
(1)丒(2)傛傝CD=CF丄佢FCD=60搙偱偁傞偐傜仮CDF偼惓嶰妏宍丅
乮亪CD=DF=FC乧(4)乯
傛偭偰丄佢ADF=10搙丅乧(5)
(3)偲佢FBC=40搙傛傝丄仮FCB偼擇摍曈嶰妏宍丅
乮FC=FB乧(6)乯
(4)丒(6)傛傝FB=DF丅亪仮FDB傕擇摍曈嶰妏宍丅
佢DFB=40搙偱偁傞偐傜佢FBD=佢FDB=70搙丅乧嘑
傛偭偰丄(5)丒(7)傛傝
佢X=佢ADF+佢FDB=80搙丅
亙姶憐亜
塸岅偺夝摎偼偒偪傫偲撉傫偱側偄偺偱偡偑丄偨傇傫暿夝摎偩偲巚偄傑偡丅
拞妛帪戙偺屆偄抦幆傪憤摦堳偟偨偺偱丄徹柧偼娫堘偭偰傞偐傕丠丠丠
亂僐儊儞僩亃
丂偙傟偼暿夝摎偱偡偹丅
惗搆偺尒杮偵側傞傎偳丄挌擩偵彂偄偰偄偨偩偄偰戝曄彆偐傝傑偡丅
偝偭偦偔惗搆偵夝摎傪尒偣偨偺偱偡偐丄塸岅偺夝摎偵偼栚傪敀崟偝偣偰傃偭偔傝偟丄偙偺夝摎偵偼戝曄婌傫偱偄傑偟偨丅
幚偼偦偺巕偼乽夝摎側傫偰偙側偄傫偠傖側偄偐乿偲尵偭偰偄偨偺偱偡丅
傑偨栤戣嶌傝偵擱偊傞偲巚偄傑偡丅
偳偆傕偁傝偑偲偆偛偞偄傑偟偨丅
仧垽抦導偺拞妛峑俀擭惗丂椻搥偽側側 偝傫偐傜偺夝摎丅
擇摍曈嶰妏宍偲嶰妏宍偺崌摨傪巊偄傑偟偨丅
俙俛傪墑挿偟丄俙俠偲摍偟偔側傞傛偆偵揰俥傪偲傞丅
俠偲俥傪寢傃丄俙俠亖俙俥偺擇摍曈嶰妏宍仮俙俠俥傪偮偔傞丅
仮俙俠俥偵偍偄偰丄佢俠俥俙亖侾侽侽亱
佢俙俠俥亖佢俙俥俠亖係侽亱
傛偭偰丄仮俛俠俥偼丄掙妏偑係侽亱偺擇摍曈嶰妏宍偱偁傞丅
師偵丄俠俥傪堦曈偲偡傞惓嶰妏宍俠俥俧傪揰俙偲斀懳懁偵偐偔丅
乮俠俥亖俥俧亖俠俧乯
俙偲俧傪寢傇偲丄仮俙俥俧佭仮俙俠俧丅
乮嶰妏宍偺崌摨忦審丗俁曈偑偦傟偧傟摍偟偄乯
佢俠俙俧亖侾侽侽乛俀亖俆侽亱
佢俙俧俠亖俇侽乛俀亖俁侽亱
佢俙俠俧亖俇侽亄係侽亖侾侽侽亱
俙俢傪墑挿偟丄俙俧偲摍偟偔側傞傛偆偵揰俫傪偲傝俙俫傪寢傇丅
偡傞偲丄仮俙俠俧佭仮俙俠俫丅
乮嶰妏宍偺崌摨忦審丗俀曈偲偦偺娫偺妏偑丄偦傟偧傟摍偟偄乯
佹俙俧亖俙俫丆佢俠俙俧亖佢俠俙俫亖俆侽亱丆俙俠亖俙俠乮嫟捠側曈乯
仮俙俠俧佭仮俙俠俫側偺偱丄
佢俙俧俠亖佢俙俫俠亖俁侽亱
佢俙俠俧亖佢俙俠俫亖侾侽侽亱
佢俢俠俫亖侾侽侽亅乮俇侽亄俀侽乯亖俀侽亱
俠俧亖俠俫
愭偵彂偄偨惓嶰妏宍偺堦曈俠俥偼丄仮俛俠俥偺堦曈偱傕偁傞丅
仮俛俠俥偼擇摍曈嶰妏宍乮忋婰乯側偺偱丄俠俥亖俠俛丅
偝傜偵丄仮俠俥俧偼惓嶰妏宍側偺偱丄俠俥亖俠俧丅
偦偟偰忋偵傕彂偄偨偲偍傝丄俠俧亖俠俫丅
傛偭偰丄俠俧亖俠俥亖俠俛亖俠俫偵側傝丄俠俛亖俠俫偵側傞丅
俠俛亖俠俫丆佢俢俠俫亖佢俤俠俫乮俁侽亱乯丆俢俠亖俢俠偱丄
仮俢俠俫佭仮俢俠俛丅
乮嶰妏宍偺崌摨忦審丗俀曈偲偦偺娫偺妏偑丆偦傟偧傟摍偟偄乯
傛偭偰丄佢俢俛俤亖俁侽亱
佢俢俛俤亖俁侽亱側傜偽丄佢俢俛俙亖俈侽亱乮係侽亄俁侽乯偵側傞丅
仮俙俛俢偵偮偄偰丄佢俢俙俛亖俁侽亱丆佢俢俛俙亖俈侽亱側傜偽丄
巆傝偺撪妏乮亖倶乯偼丄
侾俉侽亅乮俁侽亄俈侽乯亖俉侽亱偱偁傞丅
傛偭偰丂佢倶亖俉侽亱偲側傞丅