仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
栤戣偼敿宎侾侽噋丄奐偒妏係俆亱偺愵宍偵擖傞嵟戝偺惓曽宍偺柺愊傪媮傔傞偙偲偵側傝傑偡丅
偟偐偟丄愵宍偵懳偟偰偳偺傛偆側岦偒偵惓曽宍傪偲傟偽嵟戝偵側傞偺偐偑愭寛栤戣偱偡丅
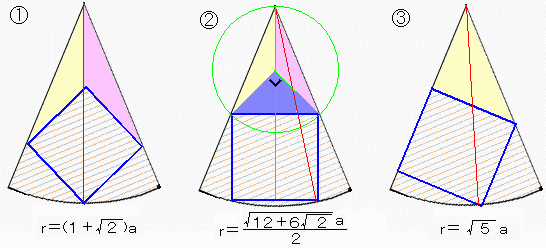
偦偙偱丄嬌抣偺壜擻惈偑梊憐偱偒傞埲壓偺俁偮偺働乕僗傪斾妑偟偰傒傑偡丅

恾偱摨怓偱揾傝偮傇偝傟偰偄傞嶰妏宍偼丄偄偢傟傕擇摍曈嶰妏宍偱偡丅
愵宍偺敿宎傪倰丄惓曽宍偺堦曈偺挿偝傪倎偲偡傞偲丄倰偲倎偺娭學幃偼忋偺傛偆偵側傝傑偡丅
乮徹柧偼徣偒傑偡偑丄僺僞僑儔僗偺掕棟傛傝梕堈偵摼傜傟傑偡乯
偙偙偱丄倎偺學悢傪俀忔偟偰俀攞偡傞偲丄
乮侾乯俇亄係![]()
乮俀乯俇亄俁![]()
乮俁乯侾侽
柧傜偐偵
俇亄係![]() 亜俇亄俁
亜俇亄俁![]() 亜侾侽
亜侾侽
偱偡偐傜丄(俁)偺働乕僗偺惓曽宍偑嵟戝偱偡丅
倰亖侾侽噋偲偡傞偲丄(俁)偺働乕僗偱偺惓曽宍偺堦曈偺挿偝偼
| 侾侽 |
噋 |
傛偭偰丄媮傔傞惓曽宍偺柺愊偼
| ( | 侾侽 |
) | 2 | 亖 | 侾侽侽 俆 |
亖俀侽 |
亂摎偊亃丂俀侽噋2
仧媨忛導丂娒愹朄巘 偝傫偐傜偺僐儊儞僩丅
Footmark 偝傫偐傜偺夝摎傪妋擣偟傑偟偨丅
偙偺愵宍撪偺惓曽宍偼墦怱曽岦偵堏摦偡傞偙偲偑偱偒傞偺偱惓曽宍偺捀揰偼墌屖忋偵偁傞偲峫偊偰傛偄丅
墌屖忋偵俀捀揰偑偁傞応崌偺嵟戝偺惓曽宍偼Footmark 偝傫偐傜偺夝摎偵偁傞偲偍傝偱偡丅
墌屖忋偵侾偮偟偐捀揰偑側偄応崌傪偲傝堦斒揑偵峫偊傑偡丅
偙偺恾宍偵倶倷嵗昗傪堷偔丅
尨揰偼捀妏丅x幉偲捈慄倷亖倶偼曈丅
墌屖偼娙扨偺偨傔敿宎傪侾偲偟偰墌倶2亄倷2亖侾丅
惓曽宍APBQ偑揰俙(倎,侽) 丄墌屖忋偺揰俹(倱丆倲)丄揰俛(倐丆倐)偱恾宍偵撪愙偡傞丅
| 0亙a亙1丆 0亙b亙 | 1 |
揰俻偑恾宍撪偵偲傟傞忦審偼丄
堦斒惈傪幐傢偢偵揰俻偑捈慄倷亖倶婑傝偲偟偰
![]() b 亜 a亜 b 丅
b 亜 a亜 b 丅
儀僋僩儖俙俹偲儀僋僩儖俛俹偑捈岎偡傞娭學幃丄
s2 - (a+b)s + ab + t2 - bt = 0
儀僋僩儖俙俛偲儀僋僩儖俹俻偺捈岎偡傞娭學幃丄
2( b-a )s + 2bt + a2 亅2b2丂= 0
揰俹偼墌廃忋偵偁傞偺偱丂s2 + t2 = 1丅
偙傟偐傜a偲倐偑枮偨偡娭學幃偼丄
| { | a 2 | + | 1 a | +b- | b2 a | } | 2 | +{( | 1 a | + | 1 b | )(b | 2 | - | a2 2 |
)+( | 1 b | - | 1 a | )(ab+1) | } | 2 | -4= 0 |
惓曽宍偺柺愊俽偼
| S = | (b-a)2 + b2 2 |
僐儞僺儏乕僞乕偱悢抣寁嶼偡傞偲揰俻偑捈慄倷亖倶忋偵偁傞応崌偑柺愊0.2偱嵟戝丅
Footmark 偝傫偐傜偺夝摎傪(1)偺(3)偺乽娫乿偺応崌傪娷傔偰妋擣偟傑偟偨丅