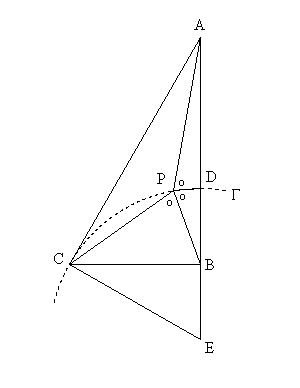
◆東京都 哲(サトシ) さんからの解答。
余弦定理より、角BPC=tとおき、
5x2-4x2cos2t=3
x2+y2-2xycost=1
4x2+y2-4xycos3t=4
を満たすことのできるt(0°<t<90°)を求めると、15°、30°、75°。
このうち15°(Pは三角形ABCの外側)、30°(PはCに一致)は無縁解であり、75°が解。
したがって、求める角の大きさは135°。
◆出題者のコメント
上記方程式よく解けましたね!
もしよかったら解き方を示していただければ幸いです。
◆大阪府 ゆたか さんからの解答。
辺ABを2:1の比に内分,外分する点をそれぞれM,Nとする。
このとき、AC:CB=AP:PB=AM:MB=AN:NB=2:1だから、
4点C,P,M,Nは同一円周上にある。(アポロニウスの円)
特に、線分MNは、この円の直径であり、∠MCN=90°である。
また、CM,PMはそれぞれ∠ACB,∠APBの二等分線であるから、
∠APM=∠MPB=∠BPC、
∠ACM=∠MCB=30°より、∠CMB=60°。
よって、∠CNM=30°となり、円に内接する四角形CPMNについて、
∠CPM=180°−30°=150°がわかる。
したがって、∠APM=∠MPB=∠BPC=75°であり、
∠APC=360°−75°×3=135°である。
◆神奈川県 いわし さんからの解答。
線分ABを2:1に内分する点をD,
ABの延長上にDB=BEとなる点Eをとる。
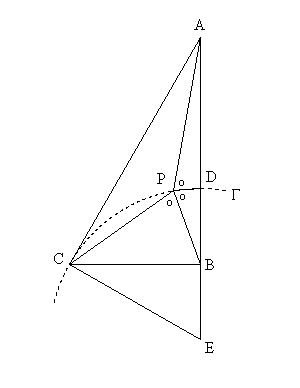
Eを中心としてDを通る円をΓとすると、
AP=2BP ⇔ PはΓ上にある。(アポロニウスの円)
∠BPC=αとおくと、AP:PB=AD:DBより、
∠APD=∠BPD=α
∠CPDはΓの優弧CDに対する円周角であり、
∠CED=60°より
∠CPD=2α=150°
∴ ∠APC=360°-3α=135°... (答)
◆出題者のコメント
私が考えていた解答は
1. アポロニウスの円を使う方法
2. 余弦定理を用いたもの
3. 別解
でした。
もともと『正三角形の面積』にあるような正三角形の問題から作ったもので、上記3の手法をまっさきに思いつきました。
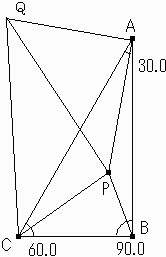
上記の手法とは
△QCA∽△PCBとなるようにQを取れば、
△QCPは60°、30°の直角三角形となり、
AQ=AP=2PBより△APQは二等辺三角形となることを利用するものです。
∠BPC+∠APB+∠APC=360°から、∠APCを求めるものでした。
(∠BPC=xとおいて、xの方程式になります)
| この問題、∠APB=k∠BPC( | 1 2 |
<k<3)ならPのような点が存在します。 |
◆静岡県 村松 芳子 さんからの解答。
∠BPC=αとおくと
∠BPA=2α,∠APB=360°−3α
PC=1とおくとAP=2
△APB,△BPC,△APCをそれぞれAB,BC,CAで折り返し、
△ADB、△BEC、△AFCを作図する。
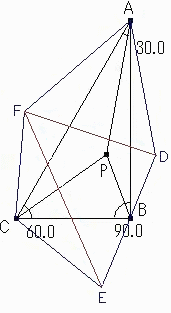
すると、∠DAF=30°x2=60°
∠DBE=90°x2=180°
すなわちDBEは直線である。
∠ECF=60°x2=120°
AD=AP=AF=2だから△AFDは頂角60°の二等辺三角形である。
すなわち△AFDは正三角形となり、DF=2である。
DB=BP=BE=1、
DBEは直線DEであり、DE=2
したがって、△DEFは二等辺三角形である。
ゆえにDFE=∠DEF
また CF=CP=CEだから△ECFは頂角120°の二等辺三角形である。
ゆえに∠CFE=∠CEF=30°となる。
∠DFE=∠AFC−60°−30°=360°−3α−90°=270°−3α
∠DEF=∠BEC−30°=α−30°
ゆえに270°−3α=α−30°
計算して、α=75°が得られる。
ゆえに∠APC=360°−3×75°=135°となる。
◆出題者のコメント
これは気づきませんでした。
逆にもし三角形ABC内部にPをとって、AB,BC,CAに関してPと対称な点をQ,R,Sとした場合、三角形QRS
が直角二等辺三角形の場合Pはどんな点になるんでしょう??