『角度の問題』

『角度の問題』解答

◆広島県　清川　育男さんからの解答。

【問題１】

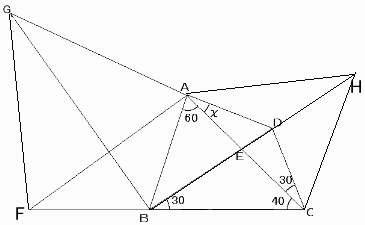
　辺ＡＢの延長線と辺ＣＤの延長線との交点をＦとする。
点Ａを通り、辺ＢＣに平行な直線と辺ＦＣとの交点をＧとする。
点Ａから辺ＦＣへの垂線の足をＨとする。

△ＡＨＦに於いて、
ＡＦ：ＦＨ：ＡＨ＝２：：１。
△ＡＣＦは二等辺三角形。
ＡＦ＝ＡＣ。

△ＥＤＡ ≡△ＧＤＡ（と仮定する）。

∠ＥＡＧ＝４０度
∠ＥＡＤ＝∠ＧＡＤ

よって∠χ＝２０度。

　　　　　　　　答え　２０度

　相似な三角形は、色々あるので、
２：：１とＡＦ＝ＦＣを使って三辺が等しい。
よって仮定は成立。となる予定ですが、なかなか難しい。
一歩、一歩進めばこの方法でも可能と思われますが、もっと上手い補助線の引き方があるのでしょうね。
図形の問題は、ヒラメキが。（ヒラメかない者の負け惜しみ。）

【コメント】

　２０度は間違いなく正解です。
ただそれを初等幾何で証明するのはなかなか難しいですね。
ぜひ証明を完成させてみてください。

◆和歌山県　宮口　祐司さんからの解答。

【問題１】

△ＡＢＣにおいて、正弦定理より、
　ＡＣ：sin８０°＝ＢＣ：sin６０°

△ＤＢＣにおいて、正弦定理より、
　ＢＣ：sin８０°＝ＤＣ：sin３０°

△ＡＤＣにおいて、正弦定理より、
　ＤＣ：sinχ＝ＡＣ：sin(１５０°－χ)

３つの式を辺々かけて、

sin８０°×sin８０°×sinχ＝sin６０°×sin３０°×sin(１５０°－χ)

以下、三角比の公式を使い、次のように計算しました。

cos１０°×cos１０°×sinχ＝sin６０°×sin３０°×sin(１５０°－χ)
(１＋cos２０°)sinχ＝sin６０°×sin(３０°＋χ)
(１＋cos２０°)sinχ＝(sin(６０°＋χ)＋sinχ)／２
(１＋２×cos２０°)sinχ＝sin(６０°＋χ)
sinχ＋sin(２０°＋χ)－sin(２０°－χ)＝sin(６０°＋χ)
２×sin(１０°＋χ)cos１０°－sin(２０°－χ)＝cos(３０°－χ)

　最後の式において、χ＝２０°がその解であるということがわかります。

図において、角度の範囲が０°より大きく７０°より小さく、一意性があることから２０°になるといえます。

mathematicaで解いてみました。

Plot[Sin[80*Pi/180]*Sin[80*Pi/180]*Sin[x*Pi/180]-Sin[60*Pi/180]*Sin[30*Pi/180]*Sin[(150-x)*Pi/180],{x,0,70}]

で、グラフは

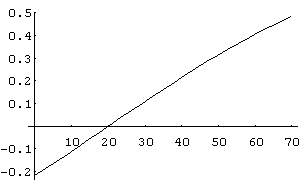
graph

角度の範囲を０°から３６０°までとすると、グラフは

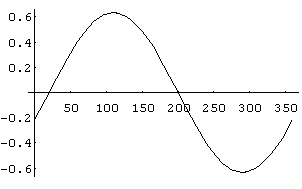
なお、数値的にmathematicaで解くと、
（これもmathematicaが持ってる機能でした）

FindRoot[Sin[80*Pi/180]*Sin[80*Pi/180]*Sin[x*Pi/180]-Sin[60*Pi/180]*Sin[30*Pi/180]*Sin[(150-x)*Pi/180]==0,{x,19,21}]

{x -> 20.}

のように、２０°が求まります。

◆神奈川県　ａｌｅｐｈさんからの解答。

初等幾何でできましたので応募してみました。
特殊な関係を見つけなければならず苦労しました。
ほかのパターンならいくつか知っているのですが。。。

【問題２の答え】２０度

【説明】

ＡＢ上に∠ＢＣＰ＝６０度になるように点Ｐをとり、ＢＤとＣＰとの交点をＱとする。

　
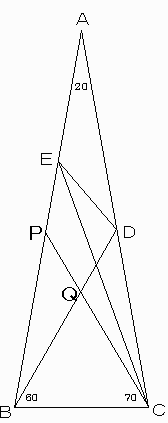
次のことを順に示し、角度を求める。

(1)△ＡＣＱと△ＣＡＥは合同。
(2)△ＰＱＥは二等辺三角形
(3)△ＰＤＥは二等辺三角形

(1)の証明

△ＡＣＱと△ＣＡＥはＡＣが共通でＡＣの両端の角度が１０度、２０度の三角形なので合同である。

(2)の証明

(1)よりＡＥ＝ＣＱ。
また△ＰＣＡはＰＡ＝ＰＣなる二等辺三角形。
したがって、△ＰＱＥはＰＥ＝ＰＱなる二等辺三角形。

(3)の証明

△ＰＱＤは正三角形。
よってＰＱ＝ＰＤ．
(2)よりＰＥ＝ＰＤ。
したがって△ＰＤＥは、頂角８０度の二等辺三角形。
したがって∠ＰＤＥ＝５０度。
したがって
∠ＤＥＣ＝∠ＰＤＥ－∠ＰＥＣ＝５０－３０＝２０度。

ＰＳ）
一般に∠ＥＢＤ＝ａ、∠ＤＢＣ＝ｂ，∠ＤＣＥ＝ｐ，∠ＥＣＢ＝ｑとし、

　ｓ＝(ｂ＋ｑ)／２、

ｔ＝ sin(a＋b＋q)×sin(p)×sin(b)
――――――――――――――――
sin(p＋q＋b)×sin(a)×sin(q)

とおくと、

∠ＤＥＣ＝ｓ＋arctan{tan(ｓ)× ｔ－１
―――――
ｔ＋１｝

となりました。

【コメント】

　問題１，２は非常によく似た問題なのですが、初等幾何で解くのは難しいですね。
この補助線一発で見通しがよくなるのには驚きました。
すばらしい証明だと思います。

◆岩手県　浮浪ぱなしさんからの解答。

「問題１」を初等幾何だけで解いてみました。
もっと簡単な方法があるような気がしてなりませんが・・・

『解答』

線分ＢＤ上に，ＢＯ＝ＣＯとなるように点Ｏを取ると，
ＢＯ＝ＣＯだから，
∠ＯＢＣ＝∠ＯＣＢ＝３０°
∠ＢＯＣ＝１２０° となる。

　
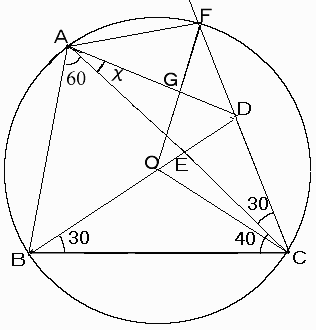
すると，∠ＢＯＣ＝１２０°，
∠ＢＡＣ＝６０°より，
Ｏは△ＡＢＣの外接円（これを円Ｏとする）の中心であることがわかる。

ここで，線分ＣＤをＤの方に延長し，円Ｏとの交点をＦとすると，
∠ＡＣＦ＝３０°より，∠ＡＯＦ＝６０°
∠ＡＢＣ＝８０°より，∠ＡＦＣ＝１００°である。

ＯＡ＝ＯＦで∠ＡＯＦ＝６０°だから△ＡＯＦは正三角形。
ゆえに，
∠ＤＦＯ＝∠ＡＦＣ－∠ＡＦＯ＝４０°である。

一方，∠ＤＯＦ＝∠ＣＤＯ－∠ＤＦＯ＝４０°なので，
四角形ＡＯＤＦは「たこ形」であることがわかる。

たこ形の対角線は直角に交わるので，
この対角線（ＡＤとＯＦ）の交点をＧとすると，
△ＡＧＯは，∠ＡＧＯ＝９０°，∠ＡＯＧ＝６０°，
∠ＯＡＧ＝３０°の三角形であることがわかる。

ところで，
ＡＯ＝ＢＯより，∠ＢＡＯ＝∠ＡＢＯ＝５０°だから
∠ＯＡＥ＝∠ＢＡＥ－∠ＢＡＯ＝１０°

ゆえに，∠χ＝∠ＯＡＧ－∠ＯＡＥ＝２０°

【コメント】

　これもすばらしい証明ですね。
もっと簡単な方法がありそうだという気持ちは分かります。
中３の知識が必要なのか疑問ですね。

◆和歌山県　中学校２年生からの解答。

【問題２】

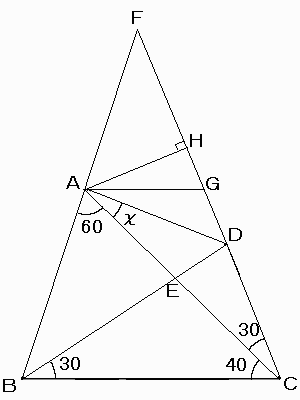
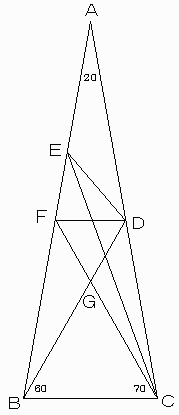点Ｄを通り、ＢＣに平行な直線をひき、辺ＡＢとの交点をＦ、ＦＣを結びＢＤとの交点をＧとする。
△ＧＢＣ及び△ＧＤＦは正三角形ゆえ、このＧは辺ＢＣの垂直二等分線上にあり、
∠ＢＧＣ＝６０°
∠ＢＥＣ＝３０°ゆえ、
∠ＢＧＣ＝∠ＢＥＣ×２となり、
点Ｇは△ＥＢＣの外接円の中心といえる。
よって、ＧＥ＝ＧＢ