◆静岡県 村松 芳子 さんからの解答。
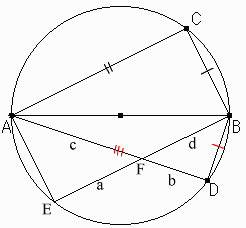
点ＡからＣＢに平行線を引き円との交点をＥとし、Ｅ、Ｂを結ぶ。
△ＡＣＢ≡△ＡＢＥ、四角形ＡＣＢＥは長方形となる。
ＢＤ＝１とするとＡＤ＝３
三平方の定理よりＡＢ＝
となる。
また△ＡＢＣでも三平方の定理を使って、
ＢＣ＝
、ＡＣ＝２。
ＡＤとＢＥの交点をＦとする。
△ＡＥＦ∽△ＢＤＦ（対頂角が等しく、もう一つの角は直角だから）
ここでＥＦ＝ａ、ＦＤ＝ｂ、ＡＦ＝ｃ、ＦＢ＝ｄとすると
ＡＥ／ＢＤ＝ａ／ｂ＝ｃ／ｄ＝／１
またａ＋ｄ＝２，ｃ＋ｂ＝３
これらを解くと
ｂ＝１，ｃ＝２，ａ＝、ｄ＝を得る。
すなわち
△ＡＥＦにおいてＡＥ＝ＥＦ、∠ＡＥＢ＝∠Ｒ
∴∠ＥＡＦ＝４５°
∴∠ＣＡＤ＝∠Ｒー４５°＝４５°
（終わり）
◆宮城県 アンパンマン さんからの解答。
∠CAD
=Arctan(1/2)+Arctan(1/3)
=Arctan(1)
=45度
◆東京都 小室 英正 さんからの解答。
円の中心をＯとし、２点Ｃ、Ｄから線分ＡＢにおろした垂線の足を、それぞれＥ、Ｆとする。
△ＡＣＢ∽△ＣＥＢ∽△ＡＥＣ、
ＡＣ：ＢＣ＝２：１より、
ＥＢ：ＥＣ：ＥＡ＝１：２：４
また、△ＡＤＢ∽△ＤＦＢ∽△ＡＦＤ、
ＡＤ：ＢＤ＝３：１より、
ＦＢ：ＦＤ：ＦＡ＝１：３：９
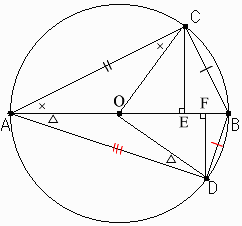
ここで、ＢＦ＝(１)とおく。
すると、△ＯＥＣにおいて、
（ＡＢ（直径）＝(１０)より、半径＝(５)に気をつければ）
ＯＥ＝(３)、ＥＣ＝(４)、ＣＯ＝(５)
また、△ＤＦＯにおいて、
ＤＦ＝(３)、ＦＯ＝(４)、ＯＤ＝(５)
よって、△ＯＥＣ≡△ＤＦＯ
したがって、
∠ＣＯＤ
＝∠ＣＯＥ＋∠ＦＯＤ
＝∠ＣＯＥ＋∠ＥＣＯ
＝９０°
∠ＯＡＣ＝∠ＯＣＡ＝×、
∠ＯＡＤ＝∠ＯＤＡ＝△とすれば、
外角の定理より∠ＣＯＤ＝××△△
よって、
∠ＣＡＤ
＝×△
＝∠ＣＯＤ÷２
＝４５°
◆海外 nymc さんからの解答。
「解答１」
直角三角形ABCにおいて
AB2
= AC2 + BC2
= (2BC)2 + BC2
= 5BC2
また直角三角形ABDにおいて
AB2
= AD2 + BD2
= (３BD)2 + BD2
= 10BD2
よって、5BC2 = 10BD2 より、
BC = *BD
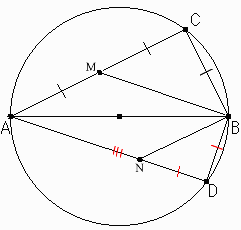
ACを２等分する点をM、ADを３等分する点のうちDに近い方をNとすると、
AM = BC、
BN
= *BD [三角形BCMは直角二等辺三角形]
= BC
よって
AM = BN
AN = 2BD、
BM
= *BC [三角形BDNは直角二等辺三角形]
=*(*BD)
= 2BD
よってAN = BM
四角形AMBNにおいて二組の対辺が等しいので四角形AMBNは平行四辺形。
したがって
∠CAD = ∠CMB [平行線の同位角] = 45度。
「解答２」
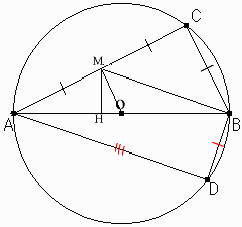
円の中心をO、ACを２等分する点をM、MからABへの垂線の足をHとすると、
∠AMO = 90度となることから、
△ABC、△AMH、△OMHは相似三角形。
したがって
AH = 2MH = 2(2OH) = 4OH
直角三角形BMHにおいて、
BH
= BO + OH
= AO + OH
= (AH + OH) + OH
= 6OH
= 3MH
直角をはさむ辺の比が等しいので（1：3）、
直角三角形BMHと直角三角形ABDは相似三角形。
よって∠MBH = ∠BAD.
錯角が等しいのでBMとADは平行。
したがって
∠CAD
= ∠CMB [平行線の同位角、三角形BCMは直角二等辺三角形]
= 45度。