三平方の定理

◆神奈川県　Alice さんからのコメント。

等積変形による三平方の定理の証明，面白く拝見しました。
ご存じかも知れませんが，三平方の定理には，アインシュタインが小学生の時に見つけたという美しい証明があります。

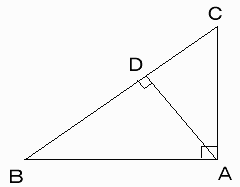
∠Ａ＝∠ＲであるΔＡＢＣの頂点Ａから辺ＢＣに下ろした垂線の足をＤとする。
ａ＝ＢＣ，ｂ＝ＣＡ，ｃ＝ＡＢとする。
ΔＡＢＣ∽ΔＤＢＡ∽ΔＤＡＣ
∴ΔＡＢＣ：△ＤＢＡ：ΔＤＡＣ＝ａ²：ｃ²：ｂ²（面積比）

∴ａ²＝ｂ²＋ｃ²

指導計画を拝見すると，三平方の定理は相似図形の面積比の次に来ているようですし，ご参考までに。

【コメント】

　証明自体は聞いたことがあると思うのですが、小学生で発見したというのが信じられません。
さすが、アインシュタイン。
数学が苦手だったといううわさも聞きましたが、一面的な見方だったのですね。

◆東京都の高校生　暇な人間さんからのコメント。

『三平方の定理の証明』

三角形ＡＢＣがあって、ＢＣ＝a、ＣＡ＝ｂ、ＡＢ＝ｃ、∠Ｃ＝９０°である。
点Ａを中心の辺ＢＣに接する円を描く。
その円とＡＢの交点をＤ、ＡＢの延長とその円の交点をＥとすると、
方べきの定理よりＢＣ・ＢＣ＝ＤＢ・ＥＢ

故にa・a＝(ｃ－ｂ)(ｃ＋ｂ)　

よって三平方の定理a²＋ｂ²＝ｃ²が成り立つ。