慄暘俛俢偲慄暘俠俤偲偺岎揰傪揰俬偲偡傞丅
揰俬偼撪怱偱偁傞丅
揰俬偐傜慄暘俛俠傊悅慄傪堷偒偦偺懌傪俥偲偡傞丅
揰俙偲揰俬傪寢傇捈慄傪慄暘俙俬偲偡傞丅
慄暘俙俬偼妏俙偺擇摍暘慄偲側傞丅
佢俛偺敿妏傪倃偲偡傞丅傑偨佢俠偺敿妏傪倄偲偡傞丅
佢俛俬俥亖俋侽亅倃.........................1)
佢俠俬俥亖俋侽亅倄.........................2)
佢俤俙俬亖佢俢俙俬亖俋侽亅(倃+倄)...............3)
佢俙俬俤亖侾俉侽亅佢俤俙俬亅佢俙俤俬
丂丂丂丂亖侾俉侽亅(俋侽亅(倃+倄))亅(俀倃+倄)
丂丂丂丂亖俋侽亅倃........................4)
佢俙俬俢亖侾俉侽亅佢俢俙俬亅佢俙俢俬
丂丂丂丂亖侾俉侽亅(俋侽亅(倃+倄))亅(俀倄+倃)
丂丂丂丂亖俋侽亅倄.........................5)
|
佢俛俬俠亖佢俛俬俥亄佢俠俬俥丆 佢俢俬俤=佢俙俬俤亄佢俙俬俢偩偐傜丄 1)4)2)5)幃偐傜佢俛俬俠亖佢俢俬俤丒丒丒乮仏乯 |
1)4)2)5)幃偲乮仏乯傛傝丄慄暘俙俬偲慄暘俬俥偼摨堦捈慄忋偺慄暘偲尵偆偙偲偵側傞丅
懄偪丄慄暘俙俥丅
仮俛俙俥偲仮俠俙俥偵偍偄偰丄慄暘俙俥偼嫟捠丅
傑偨偦偺椉抂偺妏偑摍偟偄偺偱俀偮偺嶰妏宍偼崌摨側嶰妏宍偲側傞丅
偟偨偑偭偰丄懳墳偡傞慄暘偼摍偟偄丅
懄偪丄慄暘俙俛亖慄暘俙俠.....................6)
偟偨偑偭偰丄仮俙俛俠偼擇摍曈嶰妏宍偲偄偆偙偲偵側傞丅丂
亂僐儊儞僩亃
丂弌戣幰偺悈偺棳傟偝傫偐傜丄侾乯亖係乯丄俀乯亖俆乯偺忦審偩偗偱偼丄俁揰俙丆俬丆俥偑堦捈慄忋偵偁傞偙偲偵側傜側偄偲偄偆偛巜揈偑偁傝傑偟偨丅
嶰妏娭悢傪梡偄傞徹柧偵傕嫽枴偑偁傝傑偡丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
帇妎偵傛傞旘桇傪巜揈偝傟偨偺偱偼側偄偐偲巚偄傑偡丅
揰俬傪幉偵夞揮偟偰傕娭學偼惉傝棫偮偱偼側偄偐偲尵偆偙偲偩偲巚偄傑偡丅
恾偼棟夝傪梕堈偵偡傞傕偺偱偁傞偑丄偁偔傑偱榑棟揑偵摿掕偟側偝偄偲尵偆偙偲偱偟傚偆偹丅
徹柧拞偺仩偱埻偭偨晹暘傪捛壛偟傑偡丅
偙傟偱夞揮偼側偔側傞偲巚偄傑偡丅
傕傟偑側偄偙偲傪榑棟揑偵柧傜偐偵偡傞偙偲偼尩偟偄偱偡偹丅
仧惷壀導丂儓僢僔乕偝傫偐傜偺僐儊儞僩丅
惔愳偝傫偺夝摎偱偡偑丄
佢俛俬俥亖俋侽亅倃.........................1)
佢俠俬俥亖俋侽亅倄.........................2)
佢俙俬俤亖俋侽亅倃.........................4)
佢俙俬俢亖俋侽亅倄.........................5)
偐傜偼丄
佢俛俬俥亖佢俙俬俤
佢俠俬俥亖佢俙俬俢
偑尵偊傞偩偗偱偡丅
偦偟偰丄偙傟傜偼乮偨偲偊丄俙俬俥偑捈慄偱偁偭偨偲偟偰傕乯懳捀妏偺埵抲偵側偄偺偱丄偙傟偩偗偱偼俙俬俥偑堦捈慄忋偵偁傞偙偲偼尵偊側偄偱偟傚偆丅
偦傟偵丄嵟廳梫忦審俛俢亖俠俤偑巊傢傟偰偄傑偣傫丅
丂仈巹傕偨偩崱丄峫偊拞偱偡丅
丂仈傑偩摎偊尵偭偪傖偩傔偱偡亜亜悈偺棳傟偝傫
仧媨忛導丂惸摗丂惤偝傫偐傜偺夝摎丅
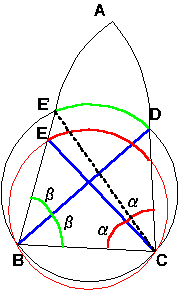 仮俙俛俠偑俀摍曈嶰妏宍偱側偄偲壖掕偡傞偲
仮俙俛俠偑俀摍曈嶰妏宍偱側偄偲壖掕偡傞偲
佢兝亗佢兛乮奺乆妏俛丄妏俠偺俀摍暘妏乯丅
傑偨戣堄傛傝丄俤俠亖俛俢偲偡傞丅
仮俢俛俠媦傃仮俤俛俠偵奜愙偡傞墌傪偦傟偧傟俼兛丄俼兝偲偟
慄暘俙俛偲墌俼兛偲偺岎揰傪俤乫偲偡傞丅
尫俤俠偑俼兝偵挘傞墌廃妏偼俀兝
尫俢俛偑俼兛偵挘傞墌廃妏偼俀兛偲側傞丅丂
墌偺戝彫傪丂俼兛亜俼兝偲婰弎偡傞偲丄奺尫EC丄俛俢偼摍偟偄偺偱
俀亊佢兛丂亙丂俀亊佢兝偲側傞丅
偲偙傠偑丄
屖俤乫俢偺墌廃妏俤乫俛俢亖佢兝亖墌廃妏俤乫俠俢偱偁傞偺偱
丂佢兛乮亖佢俤俠俢乯丂亜丂佢兝亖乮佢俤乫俠俢乯
偲側偭偰柕弬偑惗偠傞丅
傑偨丄俼兛亙俼兝偺応崌傕摨條偵側傝柕弬偡傞丅
傛偭偰丄壖掕偼岆傝偱偁傞丅
俼兛亖俼兝偺応崌丄揰俤偲揰俤乫偼摨堦偺揰偵側傞偺偱
丂俀亊佢兛丂亖丂俀亊佢兝
丂丂乮奺乆尫俢俛丄俤俠偺墌廃妏乯
偐偮
丂佢兛乮亖佢俤俠俢乯亖佢兝亖乮佢俤乫俠俢乯
丂丂乮屖俤俢偺墌廃妏乯
偲側傞丅
偡側傢偪仮俙俛俠偼俀摍曈乮俀摍妏乯嶰妏宍偱側偗傟偽側傜側偄丅
丂摨堦挿偺尫偺墌廃妏偲墌偺戝彫偺娭學偼丄墌廃妏偑俀曽岦偵偁傞偺偱丄暿搑徹柧偑昁梫偐傕偟傟傑偣傫偑偦偺傑傑巊偭偰偄傑偡丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
俢俠=俠俥 偱偁傞偐傜佢俠俢俥=佢俠俥俢
傑偨佢俢俠俛=佢俠俥俤
偟偨偑偭偰佢俢俠俛=佢俠俢俥
嶖妏偑摍偟偄偺偱丄慄暘俛俠偲慄暘俥俤偼暯峴偲側傞丅
傑偨 俛俠=俥俤偱偁傞偐傜巐妏宍俤俛俠俥偼暯峴巐曈宍偲側傞丅
偟偨偑偭偰俤俛=俠俥=俢俠
仮俤俛俠偲仮俢俠俛偵偍偄偰
俁曈偑摍偟偄偐傜仮俤俛俠偲仮俢俠俛偼崌摨側嶰妏宍偲側傞丅
偟偨偑偭偰懳墳偡傞丄佢俤俠俛=佢俢俛俠
傛偭偰佢俛=佢俠
備偊偵丄俙俛=俙俠偲側傝丄仮俙俛俠偼擇摍曈嶰妏宍偲偄偆偙偲偵側傞丅
仧搶嫗搒丂eiki偝傫偐傜偺夝摎丅
亂弨旛亃
俢偐傜曈俛俠偲暯峴側捈慄傪傂偒丄曈俙俛偲偺岎揰傪俤'
傑偨佢俙俛俠亖俀倃丄佢俙俠俛亖俀倄偲偟丄佢倃亝佢倄偲偡傞丅
侽亙倃亙俋侽亱丄侽亙倄亙俋侽亱偱偼
亂曗彆慄偺愢柧亃
俛俢亖俠俤偩偐傜俛俢sin倃亝俠俤sin倄傛傝
偡側傢偪 俠俢亝俠俢'丄俛俤'亝俛俤丄俢'俤亝俢俤' 乧乧 嘆
儮俠俢'俤偼擇摍曈嶰妏宍偩偐傜丄俠俢'亖俢'俤 乧乧 嘇
偟偨偑偭偰 嘆嘇嘊傛傝 俠俢'亝俛俤' 乧乧 嘋
亂徹柧偺娞亃
偲偙傠偱丄惓尫掕棟傛傝丄儮俠俢'俤丄儮俠俢俤'偵偍偄偰
嘍嘐傛傝 俠俢'丄俛俤'傪媮傔偰嘋偵戙擖偡傞偲
俁妏娭悢偺攞妏偺岞幃傪巊偭偰 俛俢亖俠俤丄侽亙cos倃丄侽亙cos倄偩偐傜
亂寢榑亃
乮仸乯偲嘑傪摨帪偵枮偨偡偺偱 cos倃亖 cos倄丄偡側傢偪
亂姶憐亃
壗偐僀儞僠僉偔偝偔偰帺怣偁傝傑偣傫丅
仧婒晫導丂悈偺棳傟丂偝傫偐傜偺夝摎丅
丂儮俙俛俠偵偍偄偰丄佢俛丄佢俠偺俀摍暘慄偑懳曈偲岎傢傞揰傪俢丄俤偲偡傞偲偒丄
僐儊儞僩丗
俛俠亖倎丆俠俙亖倐丆俙俛亖們丂偲偍偔丅
傑偨丄撪妏偺俀摍暘慄偺惈幙傛傝丄
傛偭偰丄
偙傟傜傪 俛俢2 傗 俠俤2 偵戙擖偟偰
丂俠俤2
偙偙偱丄
亙仏仏亜 偼暿偵寁嶼偟偰丄
僐儊儞僩丗偁偺栭傕偭偲崻婥傛偔丄場悢暘夝傪悑峴偡傟偽傛偐偭偨偺偵偲斀徣丅
仧搶嫗搒偺戝妛惗丄惎偺巕僔儊僆儞 偝傫偐傜偺夝摎丅
亂惓尫掕棟傪梡偄偨徹柧亃
娙扨偺偨傔佢俛亖俀兝丄佢俠亖俀兞偲偍偔丅
惓尫掕棟傛傝
俛俢亖俠俤傛傝
揥奐偡傞偲
俛俢亖俠俤亖俛俤'傛傝仮俛俢俤'偼擇摍曈嶰妏宍
偙偙偱兝亜兞乮忋偺徹柧偱偺掕媊傪棙梡乯偲壖掕偡傞偲
亪丂佢俠俤'俢亜佢俠俢俤'丒丒仏
偲偙傠偑
佢俠俢俤'亖180並丒兝丒俀兞丒佢俛俤'俢
兝亜兞側偺偱佢俠俤'俢亙佢俠俢俤'丒丒仏仏
仏偲仏仏偼柕弬
兝亙兞偺応崌傕摨條
柕弬傪偝偗傞偨傔偵偼兝亖兞偱側偗傟偽側傜側偄丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
俛俢偲俠俤偺岎揰傪俷偲偡傞丅
丂佢俥俢俠
丂佢俠俛俥
偟偨偑偭偰丄佢俥俢俠亖佢俠俛俥
傑偨丄佢俛俷俠亖侾俉侽搙亅(佢俷俛俠+佢俷俠俛)
偟偨偑偭偰佢俛俷俠亜俋侽搙
佢俥俢俠亖佢俠俛俥亜俋侽搙
俥俠偼嫟捠丅俛俠亖俢俥,佢俥俢俠亖佢俠俛俥
偟偨偑偭偰丄俛俥亖俢俠亖俛俤丅
仮俤俛俠偲仮俢俠俛偵偍偄偰
俛俠偼嫟捠丅俤俛亖俢俠,俤俠亖俢俛
傛偭偰擇偮偺嶰妏宍偼崌摨丅
偟偨偑偭偰丄佢俛亖佢俠
埲忋偱偡丅
仧堬忛導丂怴抾偺巕 偝傫偐傜偺夝摎丅
乮嶰妏娭悢傪梡偄偨夝摎乯
佢B=2b, 佢C=2c 偲偍偒, 仮BCD, 仮BCE 偵偍偄偰惓尫掕棟傪梡偄傞偲
壖掕 BD = CE 傛傝
偙傟偐傜 b = c 傪摫偒丆仮ABC 偑擇摍曈嶰妏宍偱偁傞偙偲傪帵偡丅
偄傑 b = M + N, c = M - N 偲偍偒丆愊傪嵎偵側偍偡岞幃傪梡偄傞偲
0 = sin(b+2c)sin(2b) - sin(2b+c)sin(2c)
0亱< 2b+2c < 180亱, 0亱< 2a < 180亱, -180亱< -2b < 0亱傛傝
偝傜偵 X = (sinM)2, Y = (sinN)2 偲偍偔偲
忋偺幃偼, 俁攞妏偍傛傃俆攞妏偺岞幃傪梡偄偰
0 = sinM sin3N + sin5M sinN
偡側傢偪 b = c
仧媨忛導丂娒愹朄巘 偝傫偐傜偺夝摎丅
佢俛丂亙丂佢俠偲壖掕偡傞丅
仮俙俤俛俠俢偲崌摨側嶰妏宍仮俹俿俻俼俽傪偮偔傝棤曉偟偰
揰俹偑仮俙俤俛俠俢偺撪晹傑偨偼廃忋偵偁傞偲偡傞偲
傛偭偰揰俹偼仮俙俤俛俠俢偺奜晹偵偁傞丅
仮俹俧俤佷仮俙俧俠
慄暘俹俤偺挿偝亙慄暘俹俼偺挿偝亖慄暘俙俠偺挿偝側偺偱
傑偨丄仮俤俼俠偺柺愊亙仮俤俛俠偺柺愊
傛偭偰丄仮俹俼俠偺柺愊亙仮俙俛俠偺柺愊丂偲側傝丂
傛偭偰攚棟朄偐傜佢俠亝佢俛
佢俛亙佢俠偲壖掕偟偰摨條偵峫嶡偟偰丄佢俛亝佢俠
偟偨偑偭偰丂佢俛亖佢俠丂偲側傝仮俙俛俠偼擇摍曈嶰妏宍偱偁傞丅
仧娾庤導丂utu 偝傫偐傜偺夝摎丅
嶰妏宍ABC偑擇摍曈嶰妏宍偱側偄偲壖掕偟丄
偡傞偲丄BD亖CE丂偐偮丂兛亙兝丂傛傝丄慄暘FD傛傝慄暘EG偺傎偆偑忋曽乮A傛傝乯偵
偁傞丅
偡側傢偪丄
仮俢俛俠偲崌摨側嶰妏宍俠俤俥偲側傞傛偆偵丄揰俥傪偲傞丅
慄暘俙俠偲慄暘俤俥偲偺岎揰傪俢'偲偡傞丅
傑偨揰俢偲揰俢'偼摨堦偺揰偱偁傞偙偲偑傢偐傞丅
俠俤=俛俢丆俤俛=俢俠丆俛俠=俠俛(嫟捠乯
俤偐傜曈俛俠偲暯峴側捈慄傪傂偒丄曈俙俠偲偺岎揰傪俢'偲偡傞丅
佢倃亝佢倄偲壖掕偟偰傕堦斒惈偼幐傢傟側偄乯
sin倃亝sin倄丄cos倄亝cos倃 乧乧 乮仸乯
乮俢偲曈俛俠偲偺嫍棧乯亝乮俤偲曈俛俠偲偺嫍棧乯
儮俠俢俤'偼擇摍曈嶰妏宍偩偐傜丄俛俤'亖俢俤' 乧乧 嘊
丂乧乧 嘍
俠俢'
sin倄= 俠俤
sin(180亱亅俀倄乯= 俠俤
sin俀倄
丂乧乧 嘐
俛俤'
sin倃= 俛俢
sin(180亱亅俀倃乯= 俛俢
sin俀倃
sin倄
sin俀倄亊俠俤 亝 sin倃
sin俀倃亊俛俢
俠俤
俀cos倄亝 俛俢
俀cos倃
cos倃亝 cos倄乧乧 嘑
乮侽亙倃亙俋侽亱丄侽亙倄亙俋侽亱偱偼 倃亖倄偩偐傜乯
儮俙俛俠偼擇摍曈嶰妏宍
摿偵晄摍幃偼偡偖岦偒偑傂偭偔傝曉偭偪傖偆偟丅丅丅
俛俢亖俠俤側傜偽俙俛亖俙俠偱偁傞偙偲傪徹柧偣傛丅
埲慜偵弌戣偟偰偍偒傑偟偨偑丄偙偺搙夝愅妛偱夝偗偨偺偱丄曬崘偟傑偡丅
場悢暘夝偺庤慜傑偱偼丄俈寧俀俆擔偺栭昹徏偺儂僥儖偱摓払偟偰偄傑偟偨丅
撪妏偺俀摍暘慄偺挿偝偺偲偒丄俛俢傗俠俤傪弌偟偨偙偲傪巚偄弌偟偰偔偩偝偄丅
偪側傒偵丄
俛俢2亖俛俠丒俛俙亅俠俢丒俢俙
俠俤2亖俠俛丒俠俙亅俛俤丒俤俙
亙仏偙傟傜偼徹柧嵪傒亜
丂俠俢丗俢俙亖倎丗們
丂俛俤丗俤俙亖倎丗倐
俠俢亖倎倐乛(倎亄們) 丆俢俙亖們倐乛(倎亄們)
俛俤亖倎們乛(倎亄倐) 丆俤俙亖倐們乛(倎亄倐)
丂俛俢2
亖倎丒們亅倎倐乛(倎亄們) 丒們倐乛(倎亄們)
亖 倎們(倎亄倐亄們)(倎亄們亅倐)乛 (倎亄們)2
亖倎丒倐亅倎們乛(倎亄倐) 丒倐們乛(倎亄倐)
亖 倎倐(倎亄倐亄們)(倎亄倐亅們)乛 (倎亄倐)2
丂俛俢2 亅 俠俤2
亖倎(倎亄倐亄們)乛(倎亄們)2 (倎亄倐)2 亙仏仏亜
丂亙仏仏亜
亖們(倎亄倐)2(倎亄們亅倐)亅倐(倎亄們)2 (倎亄倐亅們)
亖們(倎2亄俀倎倐亄倐2)乷倎亄(們亅倐)}亅倐(倎2亄俀倎們亄們2){倎亄(倐亅們)}
亖們{倎3亄倎2(倐亄們)亄倎倐(亅倐亄俀們)亄倐2(們亅倐)乸亅倐{倎3亄倎2(倐亄們)亄倎們(俀倐亅們)亄們2(倐亅們)乸
亖(們亅倐){倎3亄(倐亄們)倎2亄倎倐們亄倐們(倐亄們)乸
亖(們亅倐){倎3亄(倐亄們)倎2亄俁倎倐們亄倐們(倐亄們)乸
壖掕偺俛俢亖俠俤偐傜丄暥帤偼偡傋偰惓偩偐傜丄
丂們亅倐亖侽
備偊偵丄俙俛亖俙俠丂丂丂丂亙徹柧廔亜
俛俢
sin俀兞亖 俛俠
sin(兝亄俀兞)
俠俤
sin俀兝亖 俛俠
sin(俀兝亄兞)
sin俀兝sin(兝亄俀兞)亖sin俀兞sin(俀兝亄兞)俀sin兝cos兝乵俀cos兝sin兞cos兞亄sin兝(侾亅俀sin2兞)乶
亖俀乵俀sin兝cos兝cos兞亄(侾亅俀sin2兝)sin兞乶sin兞cos兞
曈乆惍棟偟偰係sin兝cos2兝sin兞cos兞亄俀sin2兝cos兝(侾亅俀sin2兞)
亖係sin兝cos兝sin兞cos2兞亄俀sin2兞cos兞(侾亅俀sin2兝)
堏崁偟偰係sin兝cos兝sin兞cos兞(cos兝亅cos兞)亅係sin2兝sin2兞(cos兝亅cos兞)亄俀(侾亅cos2兝)cos兝亄俀(侾亅cos2兞)cos兞丂
亖侽
0亙兝丄兞亙兾/2丂偩偐傜丂兝亗兞側傜cos兝丒cos兞亗0
嵍曈傪俀(cos兝丒cos兞)偱妱傞偲俀sin兝cos兝sin兞cos兞亅俀sin2兝sin2兞亄侾亅(cos2兝亄cos兝cos兞亄cos2兞)
亖 俀sin兝cos兝sin兞cos兞亅俀sin2兝sin2兞亄sin2兝亄sin2兞亅cos兝cos兞亅侾
亖俀sin兝cos兝sin兞cos兞亄sin2兝cos2兞亄sin2兞cos2兝亅cos兝cos兞亅侾
亖(sin兝cos兞亄sin兞cos兝)2亅cos兝cos兞亅侾
亖sin2(兝亄兞)亅俀cos兝cos兞亅侾
亖亅cos2(兝亄兞)亅俀cos兝cos兞
亖侽
忋幃偼柧傜偐偵惉傝棫偨側偄乮佹兝亄兞亙兾/俀乯偐傜丄
兝亖兞偵側傜偹偽側傜側偄丅
亂婔壗揑丠側徹柧亃
仮俙俛俠佭仮俙'俠俛
丂俢俠亜俤'俠
佢俠俤'俢亖180並丒俀兝丒兞丒佢俛俢俤'
偲偙傠偱丄偙偺夝朄偺億僀儞僩偼仮俛俢俤'偑擇摍曈嶰妏宍偱偁傞偙偲偲丄俛俢丄俛俤'偑妏擇摍暘慄偱偁傞偙偲偺柕弬揰傪擛壗偵摫偔偐偵偁傝傑偡丅
仏傪摫偔傑偱偺徹柧偼捈姶揑偵柧傜偐側偺偱徣棯偟傑偟偨偑丄惓尫掕棟傪巊傢偢偵尩枾偵徹柧偱偒傞偐偳偆偐偼妋偐傔偰偄傑偣傫丅
拞妛帪戙偵偼戙悢偱嫮堷偵夝偄偨傛偆側婰壇偑偁傝傑偡丅
仮俤俛俠傪棤曉偟偰丄俤俠偲俛俢偑廳側傞傛偆偵丄仮俥俛俢傪偲傞丅
亖佢俥俢俛+佢俛俢俠
亖佢俤俠俛+佢俛俢俠
亖佢俢俠俤+佢俛俢俠
亖佢俛俷俠
亖佢俢俛俥+佢俠俛俢
亖佢俠俤俛+佢俠俛俢
亖佢俠俤俛+佢俢俛俤
亖佢俛俷俠
佢俷俛俠亙係俆搙丄佢俷俠俛亙係俆搙
撦妏嶰妏宍俛俠俥偲撦妏嶰妏宍仮俢俥俠偵偍偄偰
傛偭偰丄擇偮偺嶰妏宍偼崌摨丅
ALEPH偝傫偺夝摎傪柾斖偵偟傑偟偨丅
撦妏嶰妏宍偺崌摨偼丄婛抦偲偟傑偟偨丅BD
sin(2c)=
BC
sin(b+2c)丆
CE
sin(2b)=
BC
sin(2b+c)
丂sin(b+2c)sin(2b) = sin(2b+c)sin(2c)丂=sin(3M-N)sin(2M+2N) - sin(3M+N)sin(2M-2N)
丂= cos(M-3N) - cos(5M+N)
2-
cos(M+3N) - cos(5M-N)
2丂= cos(M-3N) - cos(M+3N)
2+
cos(5M-N) - cos(5M+N)
2丂=sinM sin3N + sin5M sinN
偙偙偱 M = b+c
2, N =
b-c
2偱偁傞偐傜
0亱< M < 45亱, -45亱< N < 45亱
備偊偵丂0 < sinM < 1
![]()
,
-1 ![]()
< sinN < 1
![]()
0 < X < 1
2, 0 亝 Y < 1
2丂= sinM sinN {3 - 4(sinN)2}+ sinM sinN {16(sinM)4 - 20(sinM)2+ 5}
丂= 4sinM sinN {4(sinM)4 - 5(sinM)2 - (sinN)2 +2}
丂= 4sinM sinN {(1 - 2X)
2
+( 1
2- X) + ( 1
2- Y) }
偩偐傜
sinN = 0 偙偙偱 sinM > 0, (1 - 2X) 2 +( 1
2- X) + ( 1
2- Y) > 0
偟偨偑偭偰 N = b-c
2= 0
仮俙俤俛俠俢偲慄暘俤俠偲慄暘俽俻偑堦抳偡傞傛偆偵廳偹傞丅
佢俙丂亙丂佢俹偲側傝仮俙俤俛俠俢佭仮俹俿俻俼俽偵斀偡傞丅
慄暘俹俠偲慄暘俙俛偼岎揰俧偱岎傢傝揰俼偼仮俙俤俛俠俢偺撪晹偵偁傞丅
佹佢俙亖佢俹,丂佢俹俧俤亖佢俙俧俠丂懳捀妏
仮俹俧俤偺柺愊亙仮俙俧俠偺柺愊
仮俙俤俛俠俢佭仮俹俿俻俼俽偲柕弬偡傞丅
丂丂佢ABC亖俀兛丂丄佢ACB亖俀兝丂乮兛亙兝乯
偲偍偔丅
俀曈AB丄AC忋偵丄偦傟偧傟揰F丄G傪丄
慄暘FD丄EG偑丄曈BC偲暯峴偵側傞傛偆偵偲傞丅
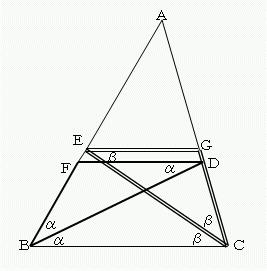
俀偮偺嶰妏宍AFD丄AEG偼憡帡偱丄嶰妏宍AEG偺傎偆偑彫偝偄偙偲偵側傞偐傜丄
丂丂FD亜EG丂丂丒丒丒丒丒丒丂仸侾
偱偁傞丅
傑偨丄暯峴慄偺嶖妏偺娭學偐傜丄
丂丂佢BDF亖佢DBF亖兛丂丄丂佢CEG亖佢ECG亖兝
偲側傞偺偱丄嶰妏宍BDF丄CEG偼偲傕偵擇摍曈嶰妏宍偱偁傞丅
偙偺俀偮偺擇摍曈嶰妏宍偼掙曈偺挿偝偑堦抳偟偰偄傞偺偱丄
掙妏偺戝偒偄傎偆偑丄懠偺俀曈偑挿偄丅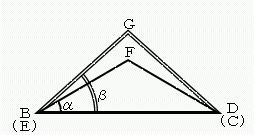
丂丂BF乮亖DF)亙EG乮亖CG)丂丒丒丒丒丒丒丂仸俀
仸侾偲仸俀偼丄偁偒傜偐偵柕弬偡傞丅
偟偨偑偭偰丄嶰妏宍ABC偼擇摍曈嶰妏宍偱偁傞丅丂乮廔乯