よって少なくとも9種あります。
(4,4,3,3,3,3)に示した2個は面の隣接状態が異なります。
従って10種としてもよい。
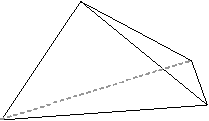
切り取り前 4面体 :
◆愛知県 Y.M.Ojisan さんからの解答。
【解答】 9種類 (以上)
どういう基準で分類すべきかという問題があります。
ここでは多面体を構成する多角形を辺数で分類したときの組合せの種類としました。
また、実際の形は4面体(1種類)から2面を切り取る方法で作りました。
この際2面の切り取り方法は、単純切断2回の場合と、りんごの芯とりのような切込みの方法があります。
6面体であるので多角形の辺数は、凸の範囲で考えると5が最大、凹までなら 特殊な6角形までが最大です。
なお、多角形6個の辺の数の合計は偶数です。
組合せを(面1辺数≧面2辺数≧面3辺数≧面4辺数≧面5辺数≧面6辺数)で表すこととします。
特殊な6角形を用いる場合は (6,6,3,3,3,3) だけが可能です。説明省略。
5角形を用いる場合は 5角形3枚以上では6面体にできません。説明省略。
以上から下表の11種類の可能性が残ります。
| 組合せ | 6面体生成可否 | |
|---|---|---|
| 1 | (3,3,3,3,3,3) | ○ |
| 2 | (4,4、3,3,3,3) | ○ |
| 3 | (4,4,4,4、3,3) | ○ |
| 4 | (4,4,4,4,4,4) | ○ |
| 5 | (5,3,3,3,3,3) | ○ |
| 6 | (5,4,4,3,3,3) | ○ |
| - | (5,4,4,4,4,3) | × |
| 7 | (5,5,3,3,3,3) | ○ |
| 8 | (5,5,4,4,3,3) | ○ |
| - | (5,5,4,4,4,4) | × |
| 9 | (6,6,3,3,3,3) | ○ |
これらのうち2種は6面体として構成することができませんでした。
よって少なくとも9種あります。
(4,4,3,3,3,3)に示した2個は面の隣接状態が異なります。
従って10種としてもよい。
切り取り前 4面体 : 
| (3,3,3,3,3,3) | (4,4,3,3,3,3) | (4,4,4,4,3,3) |
|---|---|---|
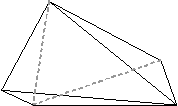 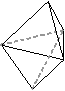 |
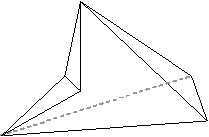 面の隣接状態が異なる。↑↓ 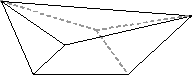 |
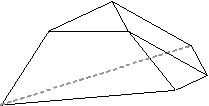 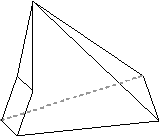 |
| (4,4,4,4,4,4) | (5,3,3,3,3,3) | (5,4,4,3,3,3) |
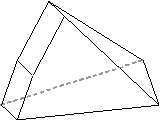 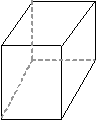 |
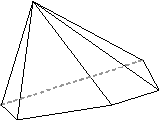 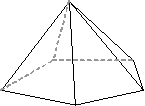 |
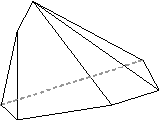 |
| (5,5,3,3,3,3) | (5,5,4,4,3,3) | (6,6,3,3,3,3) |
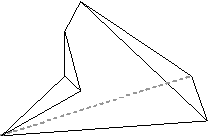 |
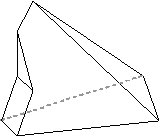 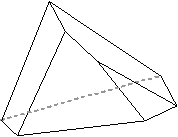 |
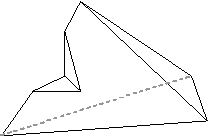 |
◆出題者の神奈川県 Alpha さんからのコメント
Y.M.Ojisan 様、いつも通り素早い回答ありがとうございます。
この問題は以前某巨大掲示板で話題になった問題の一部を切り取ってきたものです。
その問題は次のようになっております。
『単位球に内接する六面体の体積の最大値はいくらか?』
この問題を答えるとき、最初のステップとして考えるべきが本問題となります。
なお、Y.M.Ojisan 様は当然のように『どういう基準で分類すべきか?』という事に疑問を持たれたようですが
これにつきましては、出題者である私のミスでした。
申し訳ありません。
私自身、これをどう説明しようかと、悩んだのですが、高校生以下の人達が分かる言葉で説明しようとするとどうにも、上手い説明が思い浮かばず、結局今回のような出題にした次第であります。
あと、非常に難度が高くなってしまいますが、上記の問題も考えてみると面白いかもしれません。
ただし、申し訳ありませんが回答は持っておりませんのでご了承ください。
以上です。
解答ありがとうございました。
◆青木コメント
というわけで、問題を追加します。
◆愛知県 Y.M.Ojisan さんからの解答。
【追加問題解答】
| 8 9 |
(形状は予想に違わず立方体、球の約37%) |
【数値計算】
某掲示板を見ていませんが、解析的に侃侃諤諤検討されているものと考えられ、ここでは数値的にバクっと確実に検討してみました。
(1) まず、この場合の6面体の種類ですが、球に内接するものなので、その面は凸多角形で5角形以下でなければなりません。
従って(5,5,3,3,3,3)と(6,3,3,3,3,3)および凹(4、4,3,3,3,3)は除外されます。
また、辺の長さが0となる極限を考えると、
(5,5,4,4,3,3)⊃(5,4,4,3,3,3)⊃(5,3,3,3,3,3) (4,4,4,4,4,4)⊃(4,4,4,4,3,3)⊃(4,4,3,3,3,3)⊃(3,3,3,3,3,3)であるので、結局この問題の場合は6面体として (5,5,4,4,3,3)と(4,4,4,4,4,4)の2通りを検討すればよい。
(5,5,4,4,3,3)
数値計算の結果、最大状態として下図が得られました。
(2)の問題に関しては、ほぼ平面状態において最大値になっていますが、3.5度ほどのうねりが5角形にのみあり、やや大きめの値が得られていると考えられます。
(下図中●ーー●は面の法線です。)
しかし、それでも(4,4,4,4,4,4)の最大値の87%ほどしかなく、この問題の結論には影響しません。
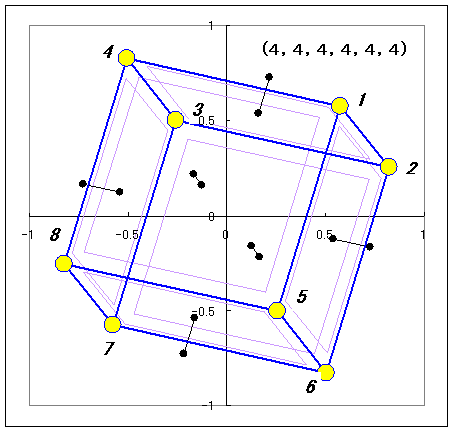
(4,4,4,4,4,4)の収束結果 詳細データ
| 面番号 | 非平面度(deg) | 面の頂点構成 | 体積 |
| 1 | 0.00 | 1,2,3,4 | 1.539600718 |
| 2 | 0.00 | 2,6,7,3 | 100% |
| 3 | 0.00 | 5,8,7,6 | |
| 4 | 0.00 | 5,6,2,1 | |
| 5 | 0.00 | 8,5,1,4 | |
| 6 | 0.00 | 8,4,7,3 |
| 頂点番号 | x | y | z |
| 1 | 0.5774 | 0.5774 | 0.5774 |
| 2 | 0.8253 | 0.2556 | -0.5036 |
| 3 | -0.2556 | 0.5036 | -0.8253 |
| 4 | -0.5036 | 0.8253 | 0.2556 |
| 5 | 0.2556 | -0.5036 | 0.8253 |
| 6 | 0.5036 | -0.8253 | -0.2556 |
| 7 | -0.5774 | -0.5773 | -0.5774 |
| 8 | -0.8253 | -0.2556 | 0.5036 |
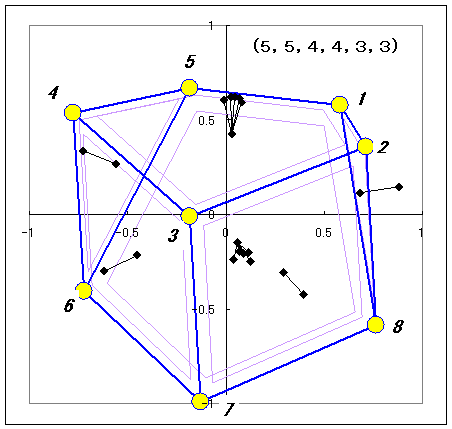
(5,5,4,4,3,3)の収束結果 詳細データ
| 面番号 | 非平面度(deg) | 面の頂点構成 | 体積 |
| 1 | 3.63 | 1.2.3.4.5 | 1.338913337 |
| 2 | 3.63 | 5,6,7,8,1 | 87% |
| 3 | 0.00 | 8,7,3,2 | |
| 4 | 0.00 | 6,4,3,7 | |
| 5 | 0.00 | 8,2,1 | |
| 6 | 0.00 | 6,5,4 |
| 頂点番号 | x | y | z |
| 1 | 0.5774 | 0.5774 | 0.5774 |
| 2 | 0.7095 | 0.3595 | -0.6061 |
| 3 | -0.1858 | -0.0113 | -0.9825 |
| 4 | -0.7768 | 0.5382 | -0.3270 |
| 5 | -0.1839 | 0.6689 | 0.7203 |
| 6 | -0.7233 | -0.4031 | 0.5607 |
| 7 | -0.1302 | -0.9897 | -0.0598 |
| 8 | 0.7630 | -0.5817 | 0.2817 |
◆出題者の神奈川県 Alpha さんからのコメント
Y.M.Ojisan様、解答ありがとうございます。
モンテカルロ法とは盲点でした。
言われてみると、モンテカルロで求めると言う手段が使えるはずですよね。
ともあれ、ありがとうございます。