
◆石川県 わさび(デビル2号) さんからの解答。
【問題1】
いえる!証明はしてません…。すんません。
長方形にならない場合とは4辺が等しい場合!
つまり、正方形orひし形だと長方形ではなく、四角形ができない。
【問題2】
4角が直角なら正方形になる。
◆大阪府 Beatle さんからの解答。
【問題1】
四角形ABCDが平行四辺形である事から
∠DAB + ∠ABC = 180°
∠NBC + ∠NCB
= (∠DAB + ∠ABC)/ 2
= 90° ・・・(1)
∴∠BNCは90°
同様に
∠ALD、∠DMC、AKBも90°
A.四角形KLMNは長方形になる
(予備)
平行四辺形ABCDの四辺の長さが同じ時向かい合う角の2等分線が重なる為、四角形KLMNは点になる。
点を四角形としないのであればこの時四角形にならない
【問題2】
三角形ALDと三角形BNCは一辺とその両端の角が同じなので合同になる。
同様に三角形AKBと三角形CMDは合同。
辺BN−辺BK = 辺AL−辺AKになるのは、
辺BN=辺AL
辺BK=辺AKの時、
つまり△NBC、BNC、AKB、CMDが二等辺三角形になった時である。
それぞれの三角形が二等辺三角形になるのは、
(1)より∠NBC=∠NCB=45°
2等分線である事から
A.平行四辺形ABCDの角が90°の時
◆鹿児島県 ともひろ さんからの解答。

平行四辺形ABCDより
直線AB//直線DCで、AB=DC
直線AD//直線BCで、AD=BC
【問題1】
長方形を作ると言える。
平行四辺形ABCDがひし形(AB=BC=AD=BC)の場合は長方形にはならない。
【長方形である、証明】
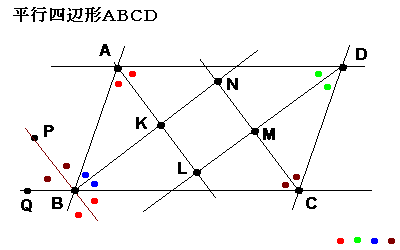
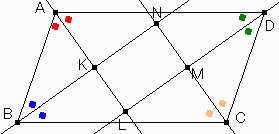
∠BCDの二等分線、直線CNに平行な直線BPを引く。
また、直線BC上でBより左側の位置に点Qをとる。
直線AD//直線BCであるから、
∠BAD=∠ABQ‥‥錯角
直線AB//直線DCであるから、
∠DCB=∠ABQ‥‥同位角
また、∠BAD=∠DCBである。
∠BAD=∠DCB=∠ABQ
ここで、∠BAD、∠DCB、∠ABQの、おのおのの角を二等分する直線AKL、直線NMC、直線BPは平行であるといえる。
∠QBP+∠PBQ+∠ABK+∠CBK=180度
(∠QBP=∠PBQ)(∠ABK=∠CBK)
2∠ABP+2∠ABK=180度
2(∠ABP+∠ABK)=180度
∠ABP+∠ABK =90度
∠BAK+∠ABK =90度
(∠BAK=∠ABP‥‥錯角)
△ABKにおいて、
∠AKB=180度−(∠BAK+∠ABK)=90度
∠NKL=∠AKB‥‥対頂角
∠NKL=90度
なお、同様に∠NML=90度とおける。
∠QBP+∠ABP+∠ABK+∠CBK=180度
∠QCM+∠DCM+∠ABK+∠CBK=180度
2∠QCM+2∠CBK=180度
2(∠QCM+∠CBK)=180度
∠QCM+∠CBK =90度
△BCNにおいて、
∠BNC=180度−(∠QCM+∠CBK)=90度
∠KML=∠BNC=90度
なお、同様に∠KLM=90度とおける。
四角形KLMNは、すべての角が直角であるから四角形KLMNは長方形であると言える。
(証明終わり)
【長方形にならない場合】
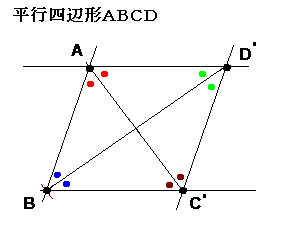
長方形にならないときは、点K,点L,点M,点Nが存在しなくなる場合、
すなわち、∠Aの二等分線と∠Cの二等分線が一致し、∠Bの二等分線と∠Dの二等分線が一致した場合。
ここで、△BC’Aにおいて、
∠BAC’=∠AC’Bであるから、△BC’Aは二等辺三角形。
△C’D’B、△D’AC’、△ABD’も二等辺三角形。
よって、AB=BC’=C’D’=D’A’である。
したがって四辺の長さがすべて等しい平行四辺形ABC’D’はひし形であるといえる。
よって、ひし形の場合は長方形KLMNは存在しない。
(説明終わり)
【問題2】
平行四辺形ABCDが、正方形でない長方形ABCDの場合、正方形KLMNが存在する。
【証明】
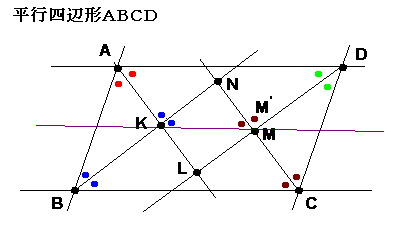
正方形KLMNとなるためには、
KL=LM=MN=NKとなる。
また、∠K=∠L=∠M=∠N=90度であるから
△KLM,△LMN,△MNK,△NKLは二等辺三角形となる。
後述のため、△MNKを△KNMとする。
ここで、点Kを通る直線BCに平行な直線KM’を引く。
(直線CNとの交点を点M’とする)
△KM’Nにおいて、
∠NKM’=∠NBC ∠NM’K=∠NCBである。
ここで、点M’が点Mと同一であり、△KM’Nが二等辺三角形になれば、長方形KLMNは正方形KLMNとなる。
そのためには
∠NKM’=∠NBC=45度
∠NM’K=∠NCB=45度となり、
∠ABC=90度 ∠BCD=90度となり、
∠BAD=90度 ∠CDA=90度となる。
したがって、平行四辺形ABCDは長方形である。
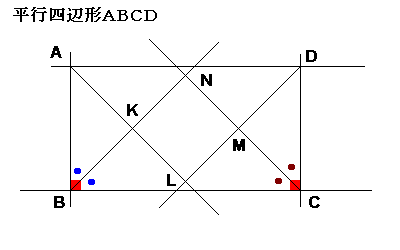
よって、長方形ABCDの場合、正方形KLMNとなる。
ただし、長方形ABCDが正方形の場合は、四角形KLMNが存在しなくなる。
平行四辺形ABCDが長方形(正方形ではない)の場合、正方形KLNMとなる。
(証明終わり)
●追記
∠K=∠L=∠M=∠Nは 長方形(正方形)KLMN 内においてのみの表現です。
◆埼玉県の中学校3年生 竜吉 公主 さんからの解答。
【問題1】
出来る。
(証明)
平行四辺形の定理より、角Aと角Bをたすと180度になる。
2等分線されているので角KABと角KBAをたすと90度になる。
三角形の外角はそれととなりあわない2つの内角の和に等しい。
角AKN=90度。
だから出来る。
【問題2】
四角形abcdが長方形のとき
◆東京都 鳳 奥人 さんからの解答。
【問題1】
長方形にならないのは、ABCDがひし形のとき。
角Aと角Cの二等分線、角Bと角Dの二等分線がそれぞれ重なってしまうから。
(というのは、この二等分線が対角線になってしまうからですね)
【問題2】
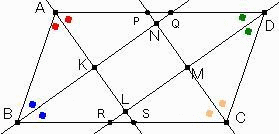
上図のように点P、Q、R、Sを定めます。
∠ABK=∠RBK=∠PQNなので
△ABQはAB=AQの二等辺三角形。
よってKはBQの中点になる。
同様に、MはCPの中点。
ABの中点をV、CDの中点をWとすると、
中点連結定理からVKはBCに平行、WMもBCに平行。
また、VWもBCに平行になる。
したがって、V・K・M・Wの4点はBCに平行な1本の直線上に存在する。
よってKMはBCに平行。
また、
∠MLN
=∠KML(KLMNは長方形だから)
=∠KBR(平行線の同位角)
=1/2∠ABR
=1/2∠CDQ
=∠CDM
したがってCDとLNは平行。
KLMNが正方形になるためには、対角線であるKMとNLが垂直になればいい。
このとき、BCとCDも垂直になる。
つまり、ABCDは長方形である。
・・・が、問題1より、ABCDが同時にひし形の特徴もそなえていたら(つまり、ABCDが正方形だったら)四角形KLMNは存在しなくなる。
というわけで、答えは
「ABCDが正方形ではない長方形であるとき」。