２
２
◆東京都 かえる さんからの解答。
【問題１】
８９と５５ ９回
【問題２】
フィボナッチ数列
ａn+2＝ａn+1＋ａn，ａ1＝ａ2＝１
の一般項を求めれば、
ａn
| ＝ | １ | （（ | １＋ ２ | ） | n | −（ |
１− ２ | ） | n | ） |
| ≒ | １ | （（ | １＋ ２ | ） | n | ） |
| （∵絶対値｜ |
１− ２ | ｜＜１） |
Ｎに含まれる最大のフィボナッチ数列がａnのとき、
ａnとａn-1を選んで、求める割り算の回数の最大値は、（n−２）回になるので、
求める割り算の回数の最大値は、
約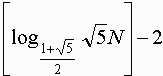
・・・【答】
[ ]はガウス記号
◆出題者のコメント。
かえるさん、ありがとうございます。
| log( |
１＋ ２ | )÷log(10) ≒ 0.2 なので、 |