◆愛知県 Y.M.Ojisan さんからの解答。
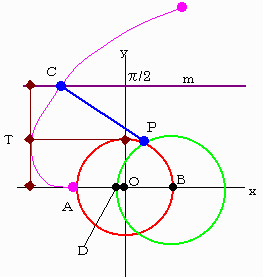
【拡張作図】で求める方法は以下である。
説明のために単位円の中心を原点Oとする座標を考える。
(1)座標の原点Oを中心とし、半径1の円を描く。
(2)x=-1,y=0の点をAとする。
(3)x=1,y=0の点をBとする。
(4)Bあたりから左周りに単位円に糸を巻きつけ、端がA点になるようにする。
(5)A点から糸をときながら先端が描く曲線A,T,C...を引く。
(インボリュート曲線)

(6)引き出した糸がx軸と平行になった点をTとする。
この時離れた糸の長さはπ/2であるが、この長さ分x軸から離れた直線mを引く。
(7)mと曲線CT...の交点をCとする。
このときの糸が単位円から離れる点をPとする。
(8)Bを中心とし、Pを通る円が単位円面積を2分する境界である。
【理論】
作図では∠AOP=Φ=CPとおくとき、
π/2=sin(Φ)−Φcos(Φ) が成立している。
一方、扇形POBの面積は (π―Φ)/2
扇形DBPの面積は (1+cos(Φ))*Φ/2
扇形の重複部分の3角形OBPの面積は
sin(Φ)/2
よって、2円で囲まれた部分の面積は
2×(扇形POBの面積+扇形POBの面積―重複部分の3角形OBPの面積) =π−Φ+Φ+Φcos(Φ)−sin(Φ) =π−(sin(Φ)−Φcos(Φ)) =π/2
◆鹿児島県 ともひろ さんからの解答。
簡易なグラフによる解法までの過程を記述します。
θを求められれば、rを求められますが、ここでは「(仮称)十進BASIC(Full JIS BASIC)」を使用して、近似値を求めています。
r=1.158728472...に至るまでの過程です。
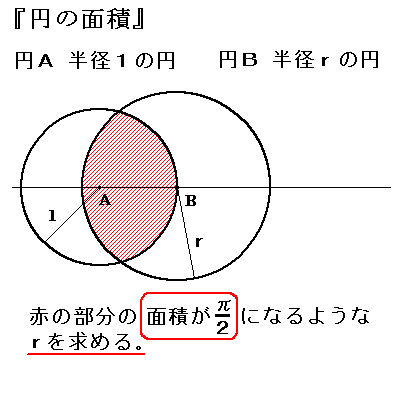
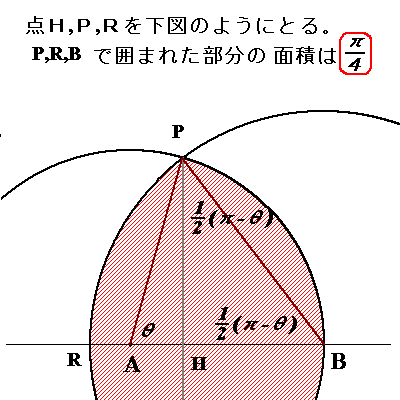
上図において、
円A(半径1の円)と、円B(半径rの円)の交点(上部)を点Pとする。
また、点Pから直線AB上に垂線を引き、この交点を点Hとする。
また、直線AB上において、円Bとの交点(左部)を点Rとする。
AB=AP=1
BP=BR=r
△ABPにおいて、∠PAB=θとすると、
AB=APであるから、△ABPは二等辺三角形。
∠APB=∠ABP=(π−θ)/2
PH=APsinθ=BPsin((π−θ)/2)
点P,点R,点Bで囲まれた部分の面積について考える。
この図形の面積は、題意の図形の面積の半分であるから、
π/4となる。
ここで、 (扇形PRBの面積)+((扇形PABの面積)−(三角形PABの面積))=π/4 となる。 (扇形PRBの面積)=π×r×r×((π−θ)/2)/2π (扇形PABの面積)=π×1×1×θ/2π (三角形PABの面積)=(1×sinθ)/2 であるから、 (π−θ)r2+2θ−π−2sinθ=0 (π−θ)r2+2θ−π=2sinθこれをy,θの関数
y=(π−θ)r2+2θ−π y=2sinθに分ける。
ここで、
「y=(π−θ)r2+2θ−π」について、
y−π
=(π−θ)r2+2θ−2π
=2(θ−π)−(θ−π)r2
=(2−r2)(θ−π)
点(π,π)を通る直線とおける。
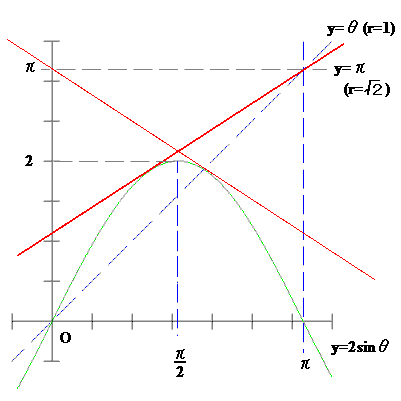
上図において、赤太線の直線は、
y=(π−θ)r2+2θ−π
で表される。
(注意)
y=(π−θ)r2+2θ‥‥(赤細線)
y=2sinθ
の接点が
y=θ上に存在しているように見えますが、これは不明。
ここで△ABPにおいて、線分BP(長さは r )は
BP2
=AP2+AB2−2・AP・AB・cosθ
AP=AB=1、であるから、
r2=2−2cosθ
r≧0であるから、
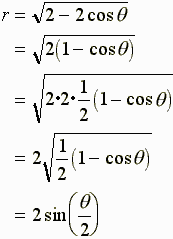
とおける。
また、y−π=2cosθ(θ−π)
rは1<r<![]() の範囲内にあり、
の範囲内にあり、
0<θ<(π/2)の範囲内において、
y=(π−θ)r2+2θ−π
y=2sinθ
が接する部分のθを求めて、
「r = 2・sin(θ/2)」に代入して、rが求められる。
(仮称)十進BASIC(JIS Full BASIC)による解
y=2sinθの接線を
「y=(π−θ)r2+2θ−π」とすることは、
求めるθでの「y=2sinθ」の接線の傾きは
「(π−2sinθ)/(π−θ)」となる。
「y = 2sinθ」をθについて微分して、
「dy/dθ=2cosθ」
方程式「(π−2sinθ)/(π−θ)=2cosθ」となる。
REM
REM 『円の面積』
REM 方程式「(π−2sinθ)/(π−θ)=2cosθ」
REM θをxとしています。
REM
LET xmin = 0
LET xmax = PI/2
LET dx=0.01
FOR i=1 TO 10
FOR x=xmin TO xmax STEP dx
LET x1=x
LET x2=x+dx
LET a1=(PI-2*SIN(x1))/(PI-x1)
LET a2=(PI-2*SIN(x2))/(PI-x2)
LET b1=2*COS(x1)
LET b2=2*COS(x2)
LET s1=SGN(a1-b1)
LET s2=SGN(a2-b2)
IF (s1<>s2)THEN
LET r1=2*SIN(x1/2)
LET c=PI-x1
LET d=2*SIN(x1)
PRINT USING "x1=##.#################### r1=##.####################":x1,r1
REM PRINT USING "x1=##.#################### r1=##.#################### c =##.#################### d =##.####################":x1,r1,c,d
LET xmin = x1
LET xmax = x2
LET dx = dx*0.1
REM (NEXT x)
EXIT FOR
END IF
NEXT x
NEXT i
END
上記プログラムでの出力
x= 1.23000000000000000000 r= 1.15799368282270000000
x= 1.23500000000000000000 r= 1.15840489342041000000
x= 1.23580000000000000000 r= 1.15869022582253000000
x= 1.23589000000000000000 r= 1.15872690459353000000
x= 1.23589600000000000000 r= 1.15872812720076000000
x= 1.23589690000000000000 r= 1.15872849398177000000
x= 1.23589692000000000000 r= 1.15872847360505000000
x= 1.23589692400000000000 r= 1.15872847319751000000
x= 1.23589692420000000000 r= 1.15872847299375000000
x= 1.23589692427000000000 r= 1.15872847301412000000
●感想
「y=(π−θ)r2+2θ−π」のグラフが
(π,π)を通ることは、rに0,1,![]() を代入したグラフ(直線)から気がつきました。
を代入したグラフ(直線)から気がつきました。
解を完全に導き出したわけではないのですが、もしかするとeやπあたりを使った簡易な式が解なのかもしれません。