◆宮城県 甘泉法師 さんからの解答。
| 偶関数 e(x)= | f(x)+f(-x) 2 |
,奇関数 o(x)= | f(x)-f(-x) 2 |
とすれば |
◆大阪府 ゆたか さんからの解答。
a(x) + b(x) = f(x),a(x)は偶関数、b(x)は奇関数とします。
a(-x) = a(x),b(-x) = -b(x) ですから、
f(-x) = a(x) - b(x) が成り立ちます。
よって、
| a(x) = | f(x) + f(-x) 2 |
,b(x) = | f(x) - f(-x) 2 |
◆出題者のコメント。
皆さんの回答を拝見させていただきました。
たくさんの回答ありがとうございました。
僕の捕らえていた回答と大体同じものだったので、たいへん安心いたしました。
しかし、僕も出題後にもう一度問題を考えてみたのですが、
以下のような関数f(x)の場合も考えられると思います。
この場合の論証はしなくてはいけないと思うのですが、どうでしょうか。
もしくは、皆さん方の証明において、このような場合はどういうことか説明できますか。
僕にはわからないのですが、誰か教えてください。
次のようなf(x)を考える。
f(x)= g_1(x)+h_1(x) (x≧0のとき)
f(x)= g_2(x)+h_2(x) (x≦0のとき)
ただし、g_(x)は奇関数、h_(x)は偶関数。
ただし、恒常的にはg_1(x)≠g_2(x)、h_1(x)≠h_2(x)とする。
このとき、
x≧0のとき
f(x)+f(-x)
= g_1(x)+h_1(x)+g_2(-x)+h_2(-x)
= g_1(x)+h_1(x)−g_2(x)+h_2(x)
f(x)−f(-x)
= g_1(x)+h_1(x)−g_2(-x)−h_2(-x)
= g_1(x)+h_1(x)+g_2(x)−h_2(x)
| このとき a(x)= | f(x) + f(-x) 2 |
,b(x)= | f(x) - f(-x) 2 |
とすると、 |
◆宮城県 甘泉法師 さんからのコメント。
>次のようなf(x)を考える。
>f(x)= g_1(x)+h_1(x) (x≧0のとき)
>f(x)= g_2(x)+h_2(x) (x≦0のとき)
をあわせて機械的に考えられるよう
θ(x)=0, x<0 ,
θ(x)=1, x≧0 を使ってあらわすと
f(x)= θ(x) { g_1(x)+h_1(x) } +(1−θ(x)){ g_2(x)+h_2(x)}
f(-x)= θ(-x) { -g_1(x)+h_1(x) } +(1−θ(-x)){ -g_2(x)+h_2(x)}
f(x)+f(-x)
= g_1(x) [θ(x)-θ(-x)] + h_1(x) [θ(x)+θ(-x)]- g_2(x) [θ(x)-θ(-x)] + h_2(x) [ 2 −θ(x)−θ(-x)]
= g_1(x) sgn(x) + h_1(x) - g_2(x) sgn(x) + h_2(x) 偶関数
f(x)-f(-x)
= g_1(x) [θ(x)+θ(-x)] + h_1(x) [θ(x)-θ(-x)]+ g_2(x) [ 2 - θ(x) - θ(-x)] + h_2(x) [ −θ(x)+ θ(-x)]
= g_1(x) + h_1(x) sgn(x)+ g_2(x) - h_2(x) sgn(x) 奇関数
ここで
sgn(x)=θ(x)-θ(-x)=-1, x<0.
sgn(x) =1, x>0. 符号関数
◆山梨県 Footmark さんからのコメント。
出題者のコメントに対するコメントです。
出題者は何か勘違いなされているのではないでしょうか?
なぜなら、甘泉法師さん や ゆたかさん の証明は任意な関数f(x)を対象にしています。
ですから、どのようなf(x)でも成立することは、既にお二人によって示されています。
このことを理解してもらうため、お二人の証明をもう少し噛み砕いてみました。
【証明】
| f(x) = | f(x)+f(x)+{f(-x)ーf(-x)} 2 |
= | f(x)+f(-x) 2 |
+ | f(x)−f(-x) 2 |
……(*) |


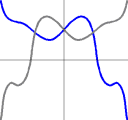
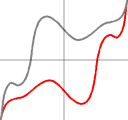
+f(-x)は、左の図のようなy軸に対して灰色のグラフと線対称な青色のグラフで、
−f(-x)は、右の図のような原点に対して灰色のグラフと点対称な赤色のグラフです。
(このとき、青色のグラフと赤色のグラフはx軸に対して互いに線対称です。)
すると、
灰色と青色の2つのグラフの和は、明らかに偶関数で、
灰色と赤色の2つのグラフの和は、明らかに奇関数です。
そこで下の図のように、これらの4つのグラフのy値をすべて半分にします。

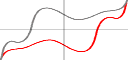
| 明らかに、左の2つのグラフの和は | f(x)+f(-x) 2 |
で、右の2つのグラフの和は | f(x)−f(-x) 2 |
ですが、 |
| よって、 | f(x)+f(-x) 2 |
は偶関数で、 | f(x)−f(-x) 2 |
は奇関数です。 |
蛇足ですがグラフで示すと以下になります。
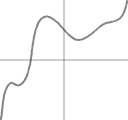 |
= |  |
+ |  |
証明は終わりです。
◆東京都 昔とった杵柄 さんからのコメント。
<f(-x)の罠?>
> 次のようなf(x)を考える。
> f(x)= g_1(x)+h_1(x) (x≧0のとき)
> f(x)= g_2(x)+h_2(x) (x≦0のとき)
> ただし、g_(x)は奇関数、h_(x)は偶関数。
出題者さんは、このように、f(x)を作って、疑問を投げられてましたが、
ポイントは、この場合には、f(-x) が、次のような式になる事だと思います。
f(-x) = g_2(-x) + h_2(-x) (x≧0のとき)
f(-x) = g_1(-x) + h_1(-x) (x≦0のとき)
ここで、x が正だと、(-x)は負なので、x≦0 の方を使う事に注意します。
つまり、x によって、式の形が変わる場合、f(-x)の式を考えるには、
f(x)の式中の「x」を、単純に「-x」に置き換えただけではいけない、という点です。
例えば、a(x) の分子部分は、このように書けます。
f(x)+f(-x) = g_1(x)+h_1(x)-g_2(x)+h_2(x) (x≧0のとき)
f(x)+f(-x) = g_2(x)+h_2(x)-g_1(x)+h_1(x) (x≦0のとき)
そして、a(-x)を考える時には、
単純に「x」を「-x」に置き換えないで、ゆっくり考えれば、偶関数である事が証明できると思います。
<余談>
もうひとつ、ひじょうに哲学的(!)な事を言う事を許してください。
解答で、 a(x) = {f(x)+f(-x)}/2 と置いていますが、この方針は「2で割り算する事ができない世界」では使えません。
例えば、大学では「標数2の体」というものを、教えてくれると思いますが、
(簡単に言えば、2の事を、0だと思い込んで作った数学の世界です。)
この場合、2と0は同じなので(!)、2で割り算する事はできないわけです。
もっとも、その時には、+1 と−1が、同じになるので(!!)、すべての関数は、奇関数でもあり、偶関数でもある事になって(!!!)、問題の結論は正しくなります。
なお、この話は、事実ではありますが、ほとんど冗談なので、気にしないで下さい。
ふつうの数学の世界では、2で割れないという事は、全然ないですので。
◆愛知県 Y.M.Ojisan さんからのコメント。
【反例】
| f(x)= | 1 x+1 |
この場合 ほとんどのxで
| e(x)= | 1 1-x2 | ,o(x)=− | x 1-x2 |
| x=1のとき,f(1)= | 1 2 | に対して |
◆出題者のコメント。
甘泉法師 さん、Footmark さん、昔とった杵柄 さん Y.M.Ojisan さん
たくさんの皆さんありがとうございました。
前の出題者のコメントの誤りがわかりました。
ご指摘ありがとうございました。
この問題を通していろんな人の考えが見えたので、とても勉強になりました。
本当にありがとうございます。
ただ、 Y.M.Ojisan さんからの解答(鋭い指摘!)のように
| 偶関数 | f(x)+f(-x) 2 |
,奇関数 | f(x)-f(-x) 2 |
| 偶関数 | f(x)+f(-x) 2 |
,奇関数 | f(x)-f(-x) 2 |
| ただし、Y.M.Ojisanさんが反例として用いた関数 | 1 x+1 |
は |
| では、偶関数 | f(x)+f(-x) 2 |
,奇関数 | f(x)-f(-x) 2 |
◆宮城県 甘泉法師 さんからのコメント。
Y.M.Ojisan さんの反例へのコメント
| f(x)= | 1 x+1 |
for x≠-1 |
| f(x)=c 定数 for x=-1 と発散しないようにすれば |
| e(x)= | 1 1-x2 |
for x≠1,-1 |
| e(x)= | c 2 |
+ | 1 4 | for x=1,-1 |
| o(x)=− | x 1-x2 |
for x≠1,-1 |
| o(x)= | c 2 |
− | 1 4 | for x=-1 |
| o(x)=− | c 2 |
+ | 1 4 | for x=1 |
◆愛知県 Y.M.Ojisan さんからのコメント。
はい、 1/(X+1)は-1において定義されていないので真の反例ではありませんでした。^^
ただ甘泉法師さんのような工夫をしないと
単純にf(x)±f(-x)で作っては良くない場合があるということです。