仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂曗戣侾亃
撌懡妏宍傪捈慄偱俀暘妱偟偨偲偒丄偦偺偄偢傟傕傑偨撌懡妏宍偱偁傞丅
乮徹柧棯乯
亂曗戣俀亃
撌懡妏宍傪擟堄曽岦偺捈慄偱擟堄柺愊斾偵俀暘妱壜擻偱偁傞丅
乮徹柧棯乯
亂曗戣俁亃
撌懡妏宍傪捈慄丗俴偱摍柺愊偵俀暘妱偟偨傕偺傪丄偝傜偵暿偺侾捈慄偱擟堄偺柺愊斾偵偦傟偧傟偺撌懡妏宍偵偍偄偰暘妱壜擻偱偁傞丅
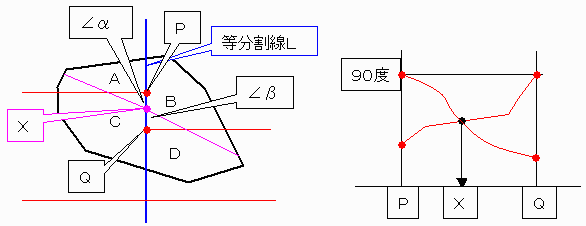
丂佹丂壓恾摍暘妱慄嵍懁傪俙丗俠偵塃懁傪俛丗俢偵暘偗傞偲偡傞丅
曗戣侾偵傛傝俙亄俠偍傛傃俛亄俢偺恾宍偼撌懡妏宍偱偁傞丅
廬偭偰丄曗戣俀偵傛傝偦傟偧傟摍暘妱慄偵捈岎曽岦偺慄偱俙丗俠丆俛丗俢偵暘妱壜擻偱偁傞丅
丂塃懁偺撌懡妏宍偵偍偄偰丄柺愊斾傪俙丗俠偵堐帩偟偮偮俴忋偺暘妱慄偺堦抂倃傪俹偐傜俻傑偱堏摦偡傞偲偒丄妏兛偼俋侽搙仺俋侽搙埲壓偵扨挷楢懕偵尭彮偡傞丅
丂摨條偵嵍懁偺撌懡妏宍偵偍偄偰丄柺愊斾傪俛丗俢偵堐帩偟偮偮俴忋偺暘妱慄偺堦抂倃傪俻偐傜俹傑偱堏摦偡傞偲偒丄妏兝偼俋侽搙仺俋侽搙埲壓偵扨挷楢懕偵尭彮偡傞丅
丂傛偭偰昁偢兛亖兝偲側傞揰倃偑俹偲俻偺娫偵偁傞丅
懄偪丄堦捈慄偱偁傞丅

亂栤戣侾亃
丂俙亖俛亖俠亖俢偲偡傟偽係暘妱壜擻偱偁傞偙偲偑暘偐傞丅
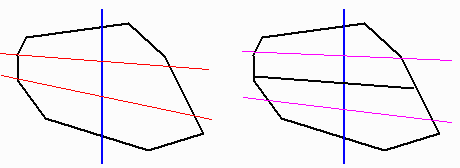
乮偪側傒偵乯丂俙亖俛亖俀丂俠亖俢亖侾丂偲丂俙亖俛亖侾丂俠亖俢亖俀丂偺俀捈慄傪堷偗偽壓恾偺傛偆偵俇摍暘妱壜擻丅
傑偨係摍暘妱偟偨傕偺傪嵞摍暘妱偡傟偽俉摍暘妱傕壜擻偱偁傞丅
亂栤戣俀亃
丂俇暘妱壜擻偱偁傞丅
乮俁捈慄偑侾揰偱岎嵎偡傞忦審壓乯
丂俙亖侾丂俛亖俀丂俠亖俀丂俢亖侾傪峫偊丄偦偺暘妱慄傪俵丄岎揰傪倃偲偡傞丅
傑偨丄俙亖俀丂俛亖侾丂俠亖侾丂俢亖俀偺暘妱慄傪俵乫丄岎揰傪倃乫偲偡傞丅
丂捈慄俴偺曽岦傪夞揮偝偣偨偲偒丄倃偲倃乫偼俴忋偱俴偺拞揰傪拞怱偵梱摦偡傞丅
偲偔偵侾俉侽搙夞揮偟偨偲偒丄俴偺拞揰傪拞怱偲偟偰懳徧側埵抲偵偔傞丅
廬偭偰丄俴偺夞揮妏侽乣侾俉侽搙偺娫偵倃偲倃乫偑堦抳偡傞揰偑偁傞丅
壓恾嶲徠
亂栤戣俁亃
丂俉暘妱晄壜擻側応崌偑偁傞丅
乮係捈慄偑侾揰偱岎嵎偡傞忦審壓乯
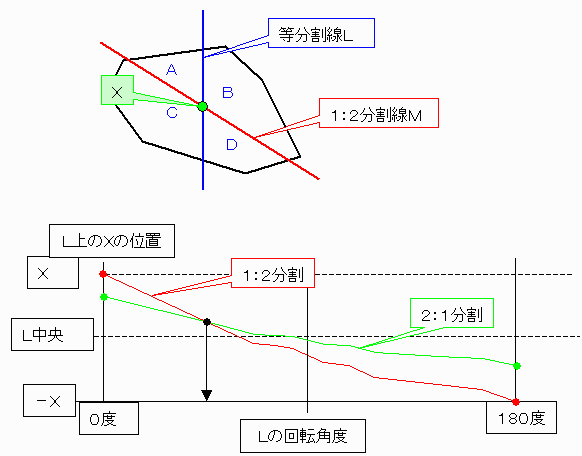
栤戣俀偲摨偠傛偆偵丂俙亖侾丂俛亖俁丂俠亖俁丂俢亖侾傪峫偊丄偦偺暘妱慄傪俵丄岎揰傪倃偲偡傞丅
傑偨丄俙亖俁丂俛亖侾丂俠亖侾丂俢亖俁偺暘妱慄傪俵乫丄岎揰傪倃乫偲偡傞偙偲偵傛傝恾宍傪侾丗俀丗侾丗侾丗俀丗侾偵俇暘妱偡傞揰偑侾揰偩偗偁傞応崌偑偁傞偙偲偑忋恾偐傜暘偐傞丅
俉摍暘妱偡傞偵偼丄俀丗俀偺斾偺晹暘傪偝傜偵丄侾丗侾丗侾丗侾偵暘妱偟側偗傟偽側傜側偄偑丄侾揰傪偲偍傞侾捈慄偱暘妱偡傞偙偲偼昁偢偟傕壜擻偱偼側偄丅
偡側傢偪丄俉摍暘妱偑偱偒側偄応崌偑偁傞丅
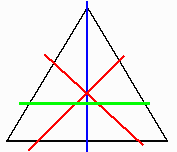
亂偱偒側偄椺丗嶰妏宍亃
仧弌戣幰偺僐儊儞僩丅
Y.M.Ojisan偝傫丄夝摎偁傝偑偲偆偛偞偄傑偡丅
偙偺栤戣丄暘妱曽朄傪帵偟偰偍偐側偐偭偨偺偼4暘妱偼偲傕偐偔丄6,8偺暘妱偵側傞偲
暘妱曽朄偑悢庬椶峫偊傜傟傞偐傜偱偁傝傑偡丅
偝偡偑偵丄Y.M.Ojisan偝傫偼婥偯偐傟偨傛偆偱偡丅
偟偐偟丄傂偲偮媈栤偑偁傝傑偡丅
6暘妱偺応崌偵偮偄偰偱偡偑丄亂栤戣侾亃偲偟偰擇摍暘偟偨屻偵
亀俙亖俛亖俀丂俠亖俢亖侾丂偲丂俙亖俛亖侾丂俠亖俢亖俀丂偺俀捈慄傪堷偗偽壓恾偺傛偆偵俇摍暘妱壜擻丅亁
偲偝傟偰偄傑偡丅
偙偙偱丄偙偺俀捈慄偼岎傢傞偙偲偺側偄俀捈慄側偺偱偟傚偆偐丠
偙偺捈慄偑撌恾宍撪偱岎傢偭偰偟傑偊偽丄偙偺徹柧偼惉棫偟側偄偙偲偵側傝傑偡丅
偝傜偵丄6暘妱偺応崌偼丄堦揰偱嶰捈慄偑岎傢傞応崌傪峫偊傞偙偲偱暘妱壜擻偲偄偆寢榑偵側傝傑偡偑
8暘妱偺応崌偼堦揰偱巐捈慄偑岎傢傞応崌丄暘妱晄壜偲偄偆寢榑偵側偭偰偟傑偄傑偡丅
傕偟壖偵丄亂栤戣1亃偺庤朄偱傕暘妱偱偒偢丄栤戣俁偺庤朄偱傕暘妱偱偒側偄恾宍偑懚嵼偟偨側傜偽
俉暘妱偼晄壜擻偲偄偆寢榑偵側傝丄偦偺傛偆側恾宍偑懚嵼偟側偄偺側傜偽俉暘妱偼壜擻偵側傝傑偡丅
偳偆偵傕
亀傑偨係摍暘妱偟偨傕偺傪嵞摍暘妱偡傟偽俉摍暘妱傕壜擻偱偁傞丅 亁
偺晹暘偑堷偭偐偐偭偰偟傑偄傑偟偰丄杮摉偵8暘妱偱偒傞偺偐偲偄偆媈栤偑惗偠偰偟傑偭偨偺偱偡丅
弌戣幰偑幙栤偡傞偺傕曄偱偡偑丄傛傠偟偗傟偽偍婅偄偟傑偡丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺僐儊儞僩丅
亂倣仜倣亃丂Alpha揳丅丂偛巜揈偛傕偭偲傕偱偡丅
傛偭偰嵞専摙偟丄埲壓偵徻嵶徹柧傪捛壛偄偨偟傑偡丅
側偍丄嵟傕尩偟偄偲巚傢傟傞嶰妏宍偺応崌偼擟堄偺係摍暘妱偵懳偟嵞暘妱壜擻側偙偲傪妋擣偟偰偍傝傑偟偨偺偱丄偦偺曽朄偵偮偄偰傕慜嵗偲偟偰婰嵹偟傑偟偨丅
亂嶰妏宍偺僋儕僥傿僇儖働乕僗亃
俴偑曈偵暯峴側応崌偼捀揰忋偱岎嵎偡傞傕偺偺丄壜擻偱偁傞丅
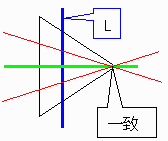
亂堦斒嶰妏宍偺応崌偺徹柧亃
丂柺愊偺斾偺傒栤戣偲偟偰偄傞偺偱慄宍曄宍偼擟堄偵壜擻偱偁傞丅
廬偭偰丄嶰妏宍傪俀摍曈嶰妏宍ABO偲偟偰傕堦斒惈傪幐傢偢丄壓婰偺嵗昗宯偱峫偊傞丅
摍暘妱慄俴傪Y幉忋俿丗(0,1)傪捠傞孹偒倱偺捈慄偲偡傞丅
傑偨丄擟堄斾偺摍斾嵞暘妱慄傪(兛,0)-(0,兝)傪捠傞捈慄偲偡傞丅
懳徧惈偐傜s偼侽乣侾偺斖埻偱慡偰傪戙昞偱偒傞丅
s=0偼忋婰僋儕僥傿僇儖働乕僗偱偁傞丅
俽倶傪壓恾偵帵偡奺晹暘柺愊偲偡傞偲偒丄
丂摍暘妱慄俴偺忦審偼丂2*(S3+S4)=S1+S2+S3+S4丂偱梌偊傜傞丅
丂摍斾嵞暘妱慄(兛,0)-(0,兝)偺忦審偼丂2*S4=S1 +S4偱梌偊傜傞丅
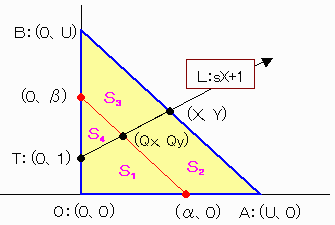
埲忋偺曽掱幃傪兝丄倀傪僷儔儊乕僞偲偟偰夝偔偲
丂 s亖侾亅係倀-1亄俀倀-2
兛亖(兝亅係亄俀兝-1)乛s
丂丂兛兝亖(兝2亅係兝亄俀)乛s丂乮亖4*俽1=4*俽4乯
偱偁傞丅
侽亙s亝1丂U亞1丂傛傝丂U亜俀亄 丂偱偁傞丅
丂偱偁傞丅
傑偨丂侽亝兛丂侾亝兝傛傝丂兝亞俀亄 丂偱偁傝丄
丂偱偁傝丄
兛'亖乮侾-俀兝-2乯乛s亜侽偱偁傞偐傜兛偼兝偵懳偟偰扨挷憹壛偱偁傞丅
偪側傒偵丄嵟戝兝亖倀偺偲偒兛亖倀偱偁傞丅
摉慠丄柺愊俽1亖俽4亖兛兝/4傕扨挷憹壛偱偁傞丅
| 偡側傢偪丄擟堄偺柺愊斾乷 | 俽1 俽1亄俽2 | 亖 | 俽4 俽3亄俽4 | 亖侽乣侾侽侽亾乸偵懳偟偰 |
 乣倀乯偼扨挷憹壛偱偁傝丄堎側傞柺愊斾偺摍斾嵞暘妱慄偑岎嵎偡傞偙偲偼側偄丅
乣倀乯偼扨挷憹壛偱偁傝丄堎側傞柺愊斾偺摍斾嵞暘妱慄偑岎嵎偡傞偙偲偼側偄丅俉摍暘偺応崌偼俀俆亾丂俆侽亾丂俈俆亾偺摍斾嵞暘妱慄傪傂偗偽傛偔丄僋儕僥傿僇儖働乕僗傪娷傔偙傟傜偼俁妏宍撪晹偱岎嵎偡傞偙偲偼側偄丅
亂堦斒撌恾宍偺応崌偺徹柧亃
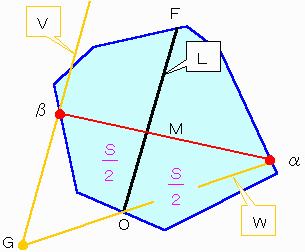
壓恾嶲徠丅柺愊斾俽偑侽亾偐傜侾侽侽亾偵曄壔偡傞偲偒丄摍斾嵞暘妱慄兛俵兝偺椉抂偺揰兛偲揰兝偑撌恾宍偺椉懁曈忋傪揰俷偐傜俥偵傓偗庛扨挷偵憹壛偡傟偽丄摍斾嵞暘妱慄偑岎嵎偡傞偙偲偼側偄偲偄偊傞丅
偙偺帠幚傪徹柧偡傞丅
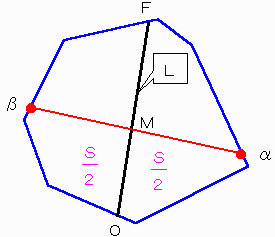
亂曗戣侾亃
揰兛傑偨偼揰兝偑俽偵懳偟偰庛扨挷偵憹壛偟側偄応崌偼丂
 乥兛俵乥亜乥兛兝乥側偄偟
乥兛俵乥亜乥兛兝乥側偄偟 乥兝俵乥亜乥兛兝乥偱偁傞丅
乥兝俵乥亜乥兛兝乥偱偁傞丅
佹俽偑憹壛偟偰兛傕兝傕尭彮偡傞偙偲偼偁傝偊側偄丅
偄傑俽偺憹壛偵懳偟偰兝偑庛憹壛偟丄兛偑尭彮偡傞偲偡傞丅
俽偑嚈俽憹壛偟偨偲偒偺摍斾嵞暘妱慄偺忬懺傪兛兝忋偺揰俹傪拞怱偵嚈兤夞揮偟偨偲偟偰昞偡偲偒
丄
兝懁偺柺愊偺憹壛嚈俽兝偼
乮乥俹兝乥2亅乥俹俵乥2乯嚈兤乛2亄o乮嚈兤2乯偱偁傞丅
堦曽丄兛懁偺柺愊偺憹壛嚈俽兛偼丂
乮乥俹M乥2亅乥俹兛乥2乯嚈兤乛2亄o乮嚈兤2乯偱偁傞丅丂
摍暘妱斾偲側傞偨傔偵偼丂嚈俽兛亖嚈俽兝亄o乮嚈兤2乯丂偱側偗傟偽側傜偢丄
乥俹兝乥2亄乥俹兛乥2亖俀乥俹俵乥2丂亄o乮嚈兤乯偱偁傞丅
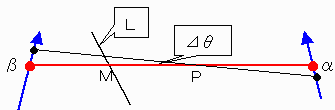
偮傑傝o乮嚈兤乯偱丄 乥俹俵乥亜乥俹兝乥偱偁傞丅
乥俹俵乥亜乥俹兝乥偱偁傞丅
偙傟偵 乥俹兛乥亜乥俹兛乥傪壛偊嚈兤仺侽偲偡傟偽丂
乥俹兛乥亜乥俹兛乥傪壛偊嚈兤仺侽偲偡傟偽丂 乥兛俵乥亜乥兛兝乥偱偁傞丅
乥兛俵乥亜乥兛兝乥偱偁傞丅
亂曗戣俀亃
 乥兛俵乥亝乥兛兝乥丂偐偮丂
乥兛俵乥亝乥兛兝乥丂偐偮丂 乥兝俵乥亝乥兛兝乥偱偁傞丅
乥兝俵乥亝乥兛兝乥偱偁傞丅
佹丂揰兝偵偍偄偰俴偵暯峴側捈慄倁傪堷偔丅
偙偺偲偒恾宍偑撌偱偁傞偙偲偐傜丄俥懁偺恾宍俥兝俵偐丄俷懁偺恾宍俷兝俵偺偄偢傟偐偺恾宍偼捈慄倁傛傝撪懁偵偁傞丅
堦斒惈傪幐傢偢崱俷懁偲偡傞丅
師偵兛偲俷傪捠傞捈慄倂傪堷偒丄倁偲偺岎揰傪俧偲偡傞丅
偙偺偲偒丂尦偺恾宍偑撌側偺偱丄
嶰妏宍兛俵俷偺柺愊亝俽乛俀亝巐妏宍兝俧俷俵丂偱偁傞丅
廬偭偰 乥兛俵乥亝乥兛兝乥偱偁傞丅
乥兛俵乥亝乥兛兝乥偱偁傞丅
兛偲兝傪擖傟懼偊傟偽摨條偵 乥兝俵乥亝乥兛兝乥偱偁傞丅
乥兝俵乥亝乥兛兝乥偱偁傞丅
亂掕棟亃
曗戣俀傛傝 乥兛俵乥亝乥兛兝乥丂偐偮丂
乥兛俵乥亝乥兛兝乥丂偐偮丂 乥兝俵乥亝乥兛兝乥偱偁傞丅
乥兝俵乥亝乥兛兝乥偱偁傞丅
廬偭偰丄曗戣侾偺媡偵傛傝揰兛偲揰兝偼俽偵懳偟庛扨挷憹壛偱偁傞丅
懄偪丄堎側傞俽偵懳偡傞慄暘兛兝偼恾宍撪晹偱岎嵎偟側偄丅
掕棟偵傛傝俽亖俀俆亾丂俆侽亾丂俈俆亾偵懳偡傞俁杮偺摍斾嵞暘妱慄兛兝傪堷偗偽丄偙傟傜偼恾宍撪晹偱岎嵎偟側偄丅
傛偭偰擟堄偺俴偵懳偟偰丄俉摍暘妱壜擻偱偁傞丅
亂俹丏俽丏亃
丂栤戣暥偺僯儏傾儞僗偐傜侾揰偱岎傢傞忦審偑敳偗偰偄傞偲巚偄崬傫偩偨傔丄捛壛晹暘偺徹柧偑偍傠偦偐偵側偭偰偟傑偄傑偟偨丅
A倢pha揳丄戝曄幐楃抳偟傑偟偨丅