『ややこしい期待値 Part２』解答

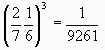
◆千葉県　永山　祐介 さんからの解答。

2から7まで、それぞれの色数になる確率を求める。
最初の一回は必ず二色選ばれるので、二回目以降で、何色増えるかによって場合分けして考える。

2色になる確率：
新しく増える色数 (0,0,0)

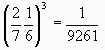
3色になる確率：
新しく増える色数 (0,0,1), (0,1,0), (1,0,0)

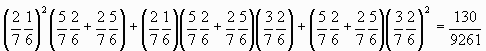
4色になる確率：
新しく増える色数 (0,0,2), (0,2,0), (2,0,0), (0,1,1), (1,0,1), (1,1,0)

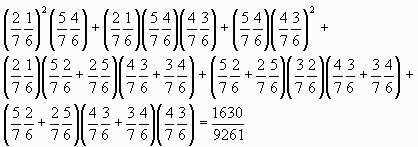
5色になる確率：
新しく増える色数 (1,1,1), (0,1,2), (0,2,1), (1,0,2), (1,2,0), (2,0,1), (2,1,0)

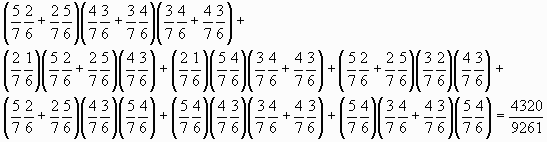
6色になる確率：
新しく増える色数 (0,2,2), (2,0,2), (2,2,0), (1,1,2), (1,2,1), (2,1,1)

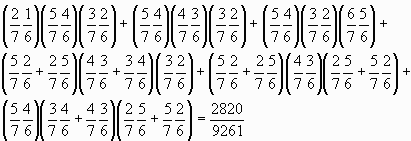
7色になる確率：
新しく増える色数 (1,2,2), (2,1,2), (2,2,1)

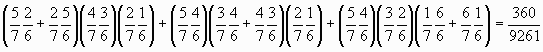
それを元に、期待値を計算する。

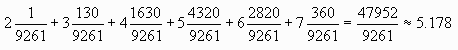
◆愛知県　Y.M.Ojisan さんからの解答。

（１）同じことですが、つぎのように計算することもできます。
ここで、Ｐijはn-1回目においてVj色の状態からn回目においてVi色になる確率です。

Pi,i=_i+1C₂、Pi+1,i=(7-i-1)*(i+1) 　 Pi+2,i=_7-i-1C₂

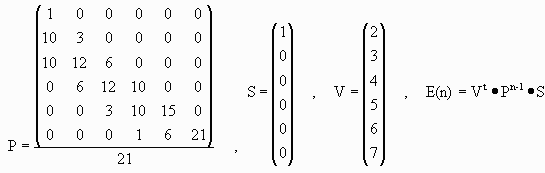
期待値はE(4)＝

1776 343

＝5.178

（２）７色状態の次の回の状態は無色になると考えた確率行列Ｑ（Ｑ₆₆=0以外Ｐと同じ）を用いると期待値は下記です。
Qの固有値は全部１未満なので収束して、下記です。
詳細参照

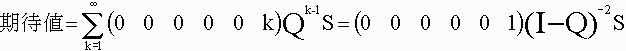
Ｉ−Ｑは三角行列なので逆行列は容易に計算でき、

期待値＝

5693 660

＝8.626

【詳細】

n-1 Σ k=0

(xQ)k

＝

(xQ)n-1 xQ-1

をｘで微分してx=1とします。

すると

n-1 Σ k=1

kQ(xQ)k-1

＝

-Q{(xQ)n-1} (xQ-1)2

＋

nQ(xQ)n-1 xQ-1

n-1 Σ k=1

k(Q)k-1

＝

1-Qn (1-Q)2

＋

nQn-1 Q-1

Ｑは下三角行列ですから固有値は対角成分であり

０〜

15 21

＜１です。

よってQⁿ→０、nQ^n-1→０{n→∞}です。

なお、(1-Q)^-1S　は(1-Q)^-1の第１列、
(0 0 0 0 0 1) (1-Q)^-1　は(1-Q)^-1の第6行で
これは(1 1 1 1 1 1)ですから、計算を節約することができます。

◆京都府　大空風成 さんからの解答。

まず、n箱から取り出したときの平均の玉の色の数を考える。 ただし、n≧4　とする。 すべての場合の数は、(7C2) n=21n　通り。 2色の玉が少なくとも1度は出る（5色の玉が出ない）のは、 特定の5色を除いた残りの2色だけをn箱から取れば、 (2C2) n=1nだから、 7C5×1n=21×1n　通り。 その確率は、 21×1n 21n ・・・(1) 3色の玉が少なくとも1度は出る（4色の玉が出ない）のは、 特定の4色を除いた残りの3色だけをn箱から取れば、 (3C2) n=3n　通りだから、 その3色のうち2色ばかり出る場合が含まれるのでそれを引くと、 7C4(3n-3C1×1n) =35×3n-105×1n　通り。 その確率は、 35×3n-105×1n 21n ・・・(2) 4色の玉が少なくとも1度は出るのは、 以下、上と同様に考えて、 (4C2) n=6n　通りだから、 7C3(6n-4C1×3n+4C2× 1n) =35×6n-140×3n+210×1n　通り。 その確率は、 35×6n-140×3n+210×1n 21n ・・・(3) 5色の玉が少なくとも1度は出るのは、 (5C2) n=10n　通りだから、 7C2(10n-5C1×6n+5C2× 3n-5C3×1n) =21×10n-105×6n+210×3n-210×1n　通り。 その確率は、 21×10n-105×6n+210×3n-210× 1n 21n ・・・(4) 6色の玉が少なくとも1度は出るのは、 (6C2) n=15n　通りだから、 7C1(15n-6C1×10n+6C2× 6n-6C3×3n+6C4×1n) =7×15n-42×10n+105×6n-140×3n+105×1n 　通り。 その確率は、 7×15n-42×10n+105×6n-140× 3n+105×1n 21n ・・・(5) 7色の玉が少なくとも1度は出るのは、 21n-7C1×15n+7C2× 10n-7C3×6n+7C4×3n-7C5× 1n =21n-7×15n+21×10n-35×6n+35×3n-21× 1n　通り。 その確率は、 21n-7×15n+21×10n-35× 6n+35×3n-21×1n 21n ・・・(6) Xを取り出される玉の色の数、P(X)をその確率とすると、 n=4　のときの確率分布は、(1)〜(6)に順に代入すると、次のようになる。 X 2 3 4 5 6 7 計 P(X) 1 9261 130 9261 1630 9261 4320 9261 2820 9261 360 9261 1 玉の色の数の平均をE(X)とすると、n=4　のときは、 E(X)= 2× 1 9261 +3× 130 9261 +4× 1630 9261 +5× 4320 9261 +6× 2820 9261 +7× 360 9261 = 47952 9261 =5 1647 9261 （色）　（約5.2色）

次に、全7色を取り出すときの平均の箱の数を考える。 n箱から取り出して、7色の玉が少なくとも1度は出る確率は、(6)より、 21n-7×15n+21×10n-35× 6n+35×3n-21 21n =1-7× ( 5 7 ) n +21× ( 10 21 ) n -35× ( 2 7 ) n +35× ( 1 7 ) n -21× ( 1 21 ) n ・・・(7) (n-1)箱から取り出して、7色の玉が少なくとも1度は出る確率は、(7)より、 1-7× ( 5 7 ) n-1 +21× ( 10 21 ) n-1 -35× ( 2 7 ) n-1 +35× ( 1 7 ) n-1 -21× ( 1 21 ) n-1 ・・・(8) n箱目で初めて全7色の玉が出たことになるのは、(7)から(8)を引けばよいから、 2× ( 5 7 ) n-1 -11× ( 10 21 ) n-1 +25× ( 2 7 ) n-1 -30× ( 1 7 ) n-1 +20× ( 1 21 ) n-1 ・・・(9) Yを全7色の玉が初めて出たときの箱の数、E(Y)をその平均とする。 E(Y)= 　 [ n k { 2× ( 5 7 ) k-1 -11× ( 10 21 ) k-1 +25× ( 2 7 ) k-1 -30× ( 1 7 ) k-1 +20× ( 1 21 ) k-1 } ] lim �� n→∞ k=4 = 2× 　 n k ( 5 7 ) k-1 -11× 　 n k ( 10 21 ) k-1 +25× 　 n k ( 2 7 ) k-1 -30× 　 n k ( 1 7 ) k-1 +20× 　 n k ( 1 21 ) k-1 ・・・(10) lim �� lim �� lim �� lim �� lim �� n→∞ k=4 n→∞ k=4 n→∞ k=4 n→∞ k=4 n→∞ k=4 ここで、r≠1　だから、 n krk-1= 4r3+5r4+・・・+nrn-1 = (4-3r)r3-rn-(1-r)nrn+1 (1-r)2 �� k=4 ｜r｜＜１のとき、ｎ→∞ ならば、ｒ ｎ→０、ｎｒｎ→０ だから、 　 n krk-1= (4-3r)r3 (1-r)2 lim �� n→∞ k=4 よって、これに r= 5 7 , 10 21 , 2 7 , 1 7 , 1 21 を代入すると、順に 1625 196 , 6000 5929 , 176 1225 , 25 1764 , 9 19600 したがって、(10)より、 E(Y)= 2× 1625 196 -11× 6000 5929 +25× 176 1225 -30× 25 1764 +20× 9 19600 = 8 413 660 （箱）　（約8.6箱） 以上より、全7色の玉を取り出すまでに要する箱の数は、 8 413 660 （箱）　（約8.6箱）

◆北海道　小西　儀紀 さんからの解答。

（PDFファイル）　

◆出題者のコメント。

永山祐介 さん、Y.M.Ojisan さん、大空風成 さん、小西儀紀 さん、解答ありがとうございます。
どの解答も模範解答のように実にみごとですね。
もちろん、全員正解です。

　『ややこしい期待値 Part２』へ

　数学の部屋へもどる