とする。
【問題1】
3角形の内角の和より x+y=43
正弦定理より
◆宮城県 甘泉法師 さんからの解答。
XY座標で、原点Oを通るx軸となす角度θ1、θ2(0<θ1<θ2)の直線L1、L2 と
点A(1,0)を通る角度π-φ1、π-φ2(0<φ1<φ2)の直線M1、M2を引く。
θ1+φ1<π、θ2+φ2<π、φ2-φ1= χとする。
直線L1とM1の交点Pの座標は
| P ( | tanφ1 tanθ1+ tanφ1 |
, | tanθ1tanφ1 tanθ1+ tanφ1 |
) |
直線L2とM2の交点Bの座標は
| B ( | tanφ2 tanθ2+ tanφ2 |
, | tanθ2tanφ2 tanθ2+ tanφ2 |
) |
△OABを題意の三角形、点Pを内部の点にとると、χが求める角度。
(1)を例に対応を示すと
θ1=77度
θ2=77+17=94度
φ1=26度
ζ=17度
χ=?度
線分PBの角度をηとする。
tanη
| = | tanθ2tanφ2 / (tanθ2+ tanφ2) - tanθ1tanφ1 / (tanθ1+ tanφ1) tanφ2 / (tanθ2+ tanφ2) - tanφ1 / (tanθ1+ tanφ1) |
| = | (tanθ1+ tanφ1)tanθ2tanφ2 - (tanθ2+ tanφ2)tanθ1tanφ1 tanθ1tanφ2 - tanθ2tanφ1 |
線分PBと直線L2のなす角ζは ζ = η-θ2
| tanη = tan(ζ+θ2) = | tanζ + tanθ2 1 - tanζtanθ2 |
両式の右辺を等しいとおいてφ2について解いて
| χ= arctan( | T S | ) - φ | 1 |
ここで
S=tanθ1(tanθ2+tanζ)-{tanθ1tanθ2+(tanθ2-tanθ1)tanφ1}(1-tanθ2tanζ)
T=tanθ2tanφ1(-tanθ1+tanθ2+tanζ+tanθ1tanθ2tanζ)
【コメント】
一般式を導きました。
(1)〜(4)の場合に解が簡単な値になるかどうかはわかりません。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】 13度
【問題2】 73度
【問題3】 73度
【問題4】 34度
問題1〜3は 最下段の3図のように補助線(赤線)を入れることで証明できましたが、問題4はうまく行かず、正弦定理で解きました。
以下証明は、正弦定理を用いた解答に統一しています。なお、角度の単位は度です。
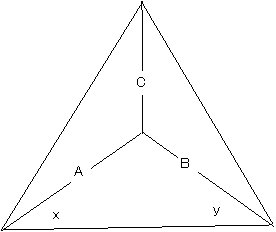
【証明】

とする。
【問題1】
3角形の内角の和より x+y=43
正弦定理より
| A sin(y) |
= | B sin(x) |
, | C sin(2*13) |
= | A sin(90-13) |
, | C sin(17) |
= | B sin(17) |
| sin(x) sin(y) |
= | sin(2*13) cos(13) |
= | 2sin(13)cos(13) cos(13) |
= | sin(13) 0.5 |
= | sin(13) sin(30) |
| A sin(y) |
= | B sin(x) |
, | C sin(2*17) |
= | A sin(13) |
, | C sin(17) |
= | B sin(13) |
| sin(x) sin(y) |
= | sin(2*17)sin(13) sin(13)sin(17) |
=2cos(17)= | sin(73) sin(30) |
| A sin(y) |
= | B sin(x) |
, | C sin(2*17) |
= | A sin(17) |
, | C sin(13) |
= | B sin(30) |
| sin(x) sin(y) |
= | sin(2*17)sin(30) sin(17)sin(13) |
= | cos(17) sin(13) | = | sin(73) sin(13) |
| A sin(y) |
= | B sin(x) |
, | C sin(3*13) |
= | A sin(47) |
, | C sin(13) |
= | B sin(30) |
| C cos(3θ) |
= | A sin(30+θ) |
, | C sin(30-θ) | =2B |
| sin(x) sin(y) |
= | cos(3θ) 2sin(30+θ)sin(30-θ) |
=2*cos(θ)= | sin(2θ) sin(θ) |
【PS】
ヒントと違う方向になりましたが、こういう方法もあるということで。
【幾何の場合】
詳細略
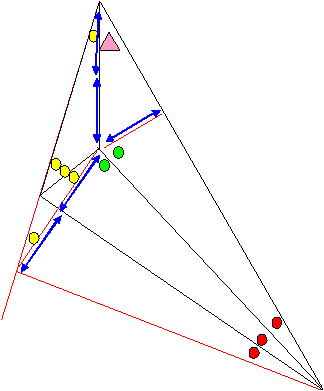
<問題1幾何解>
赤○:13度、緑○:77度、黄色○:17度、青四角:90度
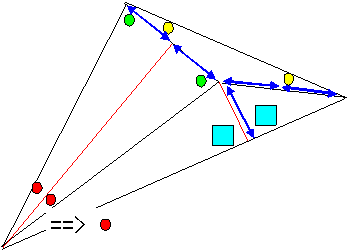
<問題2幾何解>
赤○:13度、桃△:30度、黄色○:17度、青六角:60度
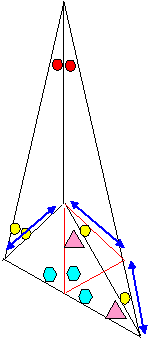
<問題3幾何解>
赤○:13度、桃△:30度、黄色○:17度、緑○:77度