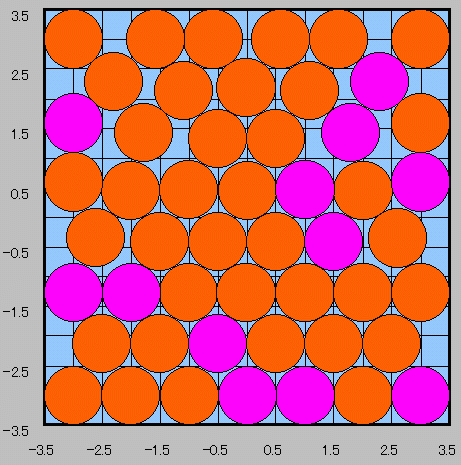
◆愛知県 Y.M.Ojisan さんからの解答。
N=8ならば 「こんな詰め方ではまだまだですね」で入りましたので、
N=7、50個に挑戦しました。
しかし、現在のところまだ成功していません。
ここでは、これまでで最善のものを下記に示します。
N=7 で D=0.99915 の円 50個です。

◆静岡県の高校生 kanjist さんからの質問。
すみません。解答ではなく質問です。
Y.M.Ojisanさんの方法は単純な規則性の並べ方でないのにもかかわらず、D=0.99915という細かい精度で計算されており感銘を受けたのですが、一方その数値がどのような方法で求められたのかを示してくださらないと、その数値がど
のくらい正しいのか僕には判断できません。
できればその点についてお答えお願いします。
僕もDを1に近づけるようにいろいろやっているのですが、規則的な並べ方では限界がきています。
ご教示お願いいたします。
◆愛知県 Y.M.Ojisan さんからのコメント。
【計算の方法】
単なる数値模擬です。
倍精度計算で行っています。
倍精度は15桁の精度があり、円は全部で50個なので桁落ちしても高々3桁です。
即ち、解答に示した桁数は十分精度があります。
最初に中心点を与え、直径を徐々に増加させます。
隣接の円にぶつかったら、空いている方向を探し、可能ならずらしてやります。
この方法により、いわゆる極大点のようなものが結果として得られます。
最大点の探索はコンピュータでなはなく、人間のカンによっています。
模擬の結果である中心点の分布を人間がみて、何点かを空間的に空いているようなところに移動させてまた模擬 し。。。として得られた結果です。
いわば四角い箱にパチンコ玉を押し込み、はみ出した玉を移動させては押し込む感じの模擬計算です。
◆神奈川県 いわし さんからのコメント。
http://hydra.nat.uni-magdeburg.de/packing/packing.html
の"Circles in a square"によると、
辺の長さが1の正方形に、50個詰め込める円の半径の現在知られている最大値rは
0.07137...で、1/(7*2)=0.07142...ですから、わずかに足りません。
(ちなみに、r/(1/14)=0.99927... なので、Y.M.Ojisan さん惜しい!)
65個なら、r=0.06320...>0.0625=1/(8*2)ですから入りますね。
◆愛知県 Y.M.Ojisan さんからのコメント。
いわし さんありがとうございます。
これですっきりしました。
配置的には合っているようなので、現状のソフトでも目標値を1.0000から0.99927に変更すればさらに肉薄できると思いますが、ここで幕とします。
◆静岡県 kanjist さんからの解答。
わざわざ回答いただいたのに返事が送れてすみませんでした。
Y.M.Ojisanさん、いわしさん、ありがとうございます。
いわしさんの教えてくださったページ「Packomania」のリンクから
http://home.att.net/~donovanhse/Packing/index.html
というページを見つけそこでY.M.Ojisanさんが自作なされたソフトと同種のソフト(Pack.exe)がありましたので、僕も試してみました
。
(楽をしてすみません)
僕の現時点での最善のものを載せておきます。
Y.M.Ojisanさんのとほぼ同じ並べ方ですが、おかげさまで少し進歩しました。
「Packomania」に出ていた最高記録はr/Sが0.071377103865ですので及びませんが…。
しかし、現時点何度も繰り返した結果では、配置的にはもうこの形で詰めていくほかないような気がしますが、
逆に、この形で詰めていくとするとr/Sが0.07137…が0.07142…まで増えていくようには思えません。
もっと効率のいい配置があるのか。それとも無理なのか……。もう少し粘ってみます。
