◆山梨県 Footmark さんからの解答。
任意の2つの部分集合S(i),S(j)における共通要素の個数f(i,j)の、最大値Mを最小にするには、
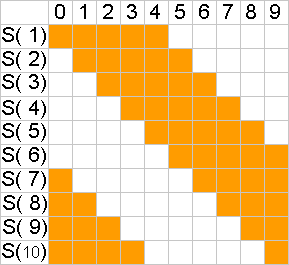
0〜9の10要素の内の5要素がS(1)〜S(10)の各部分集合に均等に偏るようにすればよい。
図はその1例である。

図からも明らかなように、このとき M=4。
よって、求めるMの最小値=4。
◆愛知県 Y.M.Ojisan さんからの解答。
【解答】 答え 3
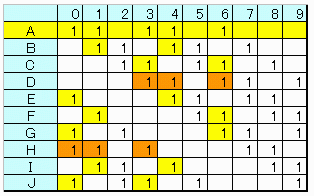
たとえば下図 A〜Jグループにする。
全てAのシフトであるので、Aに対する∩要素のみをチェックしてある。
【証明】
M=2では不可能であることを示します。
【おおよその証明】
全部で10×5個の要素が必要で、各数字を一様に使用すると、各数字5個ずつの使用である。
するとグループ間で重複するものを線で結んだ結合線の数は
10×5C2=100である。
一方、最大が2であるとすると、全体で許容される結合線の数はグループ間の組み合わせ数×2 であり
10C2×2=90<100である。
すなわち結合線が不足である。
よってM=2は不可能である。
【一様な使用が最小の証明】
50個を 50=p0+p1+p2〜p9に分けたとき
結合線の数の合計ΣpiC2を最小にするpiは
ΣpiC2=Σpi2/2−25 を最小にするpiである。
10Σpi2=(Σpi)2+Σ(pi−pj)2≧502
よりpiが同じ値である時最小であり、pi=5が最小値を与える。
【感想】
私には新鮮で興味深い問題と思いました。
◆山梨県 Footmark さんからのコメント。
なるほど、最小値は3でも可能でしたか。
ただ均等に偏っただけではダメでしたね。(^^;
この問題はとても面白いですね。
明らかに、1010101010を1つずつずらしたのでは5になってしまいます。
また、私のように単純に1111100000を1つずつずらしたのでは4になってしまいます。
試しに、1101011000を1つずつずらしてみると、これもやっぱり4でした。
どうして、Y.M.Ojisan さんが示したように、1101101000を1つずつずらすと3になるのでしょう?
そこで追加問題。
◆愛知県 Y.M.Ojisan さんからの解答。
【追加問題1】
直接の解答では無いですが、作り方をいくつか。
【M1】
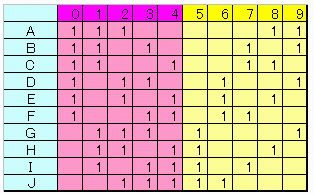
5個ずつ2グループ(下図 紫と黄)にわけ、3個と2個を分布させます。
5C3=5C2=10であり、いずれも丁度10とおりあります。
紫3個のグループでは最大2個しか重複せず、黄2個のグループでは最大1個です。
従って両方で最大3個です。
紫グループと黄グループの組み合わせだけでも 10!とおりになります。
【M2】
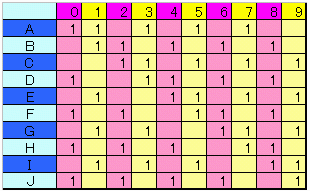
奇数か偶数かで5個ずつ2グループ(下図 紫と黄)にわけ、Aにおいてそれぞれ4個と1個を配置し、以後1づつシフトさせます。
奇数シフト差の場合、4個と1個のグループ間では最大1個しか重複しませんから、両方で最大2個です。
一方偶数シフト差の場合、4個グループ同士では最大3個重複し、1個グループ同士では重複しないので合計最大3個になります。
【M3】
M2と同様、奇数か偶数かで5個ずつ2グループ(下図 紫と黄)にわけ、Aにおいてそれぞれ3個と2個を配置し、以後1づつシフトさせます。
奇数シフト差の場合、3個と2個のグループ間では最大2個重複するので、両方で最大4個の可能性があり、さらに条件が必要です。
一方偶数シフト差の場合、3個グループ同士では最大2個重複し、2個グループ同士では1個が重複なので合計最大3個になります。
条件としては、3個の方を固定しておいて、2個のほうを前後に奇数シフトして得られた下図(1,3,5,7,9欄)において、重複が4個になる2,1,1を選ぶ、ないし2,2を含む組み合わせである(1,3,9)と(5,7,X)を除く6通りの選び方がOKとなります。
なお、偶数グループを0と4にとるケースも同様です。
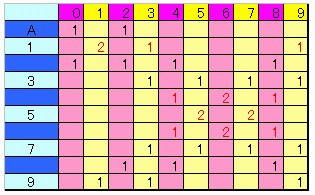
【追加問題2】 30個
実例としては 次のA1、A2,A3およびそれらを回転シフトしたもの3×10個。
なお、これらはM2,M3の方法の援用で得たものです。
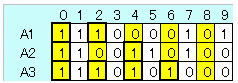
【30が最大の証明】
(1) ある3個が互いに重複するグループの数は最大3個です。
なぜなら残り2個を7種の中から重複せず選択しなければならず、
7/2=3あまり1だからです。
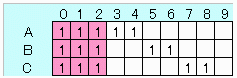
(2) そういう数字3個の組み合わせは 10C3=120とおりです。
(3) そういう3個の組み合わせ中の結合線の数は3×3=9ですから、
120×9=1080以上の結合線は存在しえません。
(4) 一方、問題1に示したように結合線の数が最小となる
おのおのn/2前後個ずつ用いた場合の結合線の数は
5[n/2][(n-1)/2]です。
(5) 計算すると n=30の時1050<1080で
n=31のとき1125>1080です。
よって30が最大です。
【追加問題3】 5個
【6個以上不可能の証明】
6個でできないものはそれ以上ではできない。
従って、6個では不可能であることを示す。
(1) ある3個が互いに重複するグループの数は最大2個です。
なぜなら残り3個を7種の中から重複せず選択しなければならず、
7/3=2あまり1だからです。
(2) そういう数字3個の組み合わせは 10C3=120とおりですが、
一方ABのようなグループの組み合わせはnC2以下である必要もあり、
n=10のときは45とおりが最大です。
(3) そういう組み合わせ中の結合線の数は=3ですから、
45×3=135以上の結合線は存在しえません。
(4) 一方、問題1に示したように結合線の数が最小となる
おのおの0.6n前後個ずつ用いた場合の結合線の数は
5(0.6n)(0.6n-1)以上です。
(5) n=10の時計算すると150であり、135より多いので不可能です。
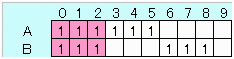
ちなみにn=5のとき 5*3*2=30 ≡ 3*5C2=30 であり6個でも可能性ありとなります。
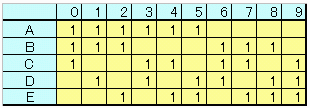
実際下図のように、考える方向を変えてA〜Eから3個取り出す組み合わせ全部により、きれいな形で可能です。
【P.S.】
追加問題4 は挑戦中です。
5と10 、2003と1338004は3m-1とm(3m-1)と考えられ、01の乱数列での期待値を考えると、この式中の3が3個重複と結びつきます。
実際 8と24 や11と44はでは容易にシフトでOKのものが見つけられました。
「2003」が用いられているので、新年問題として正月に再トライしてみます。