『球面に内接する四面体』解答

◆山梨県　Footmark さんからの解答。

【答え】

３

【証明】

図は、四面体ＡＢＣＤを頂点Ａ側から見たものです。

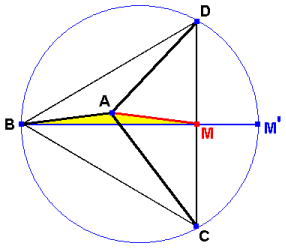
辺ＣＤの中点をＭ、ＢＭの延長線と△ＢＣＤの外接円との交点をＭ'とすると、
△ＢＣＤも△ＡＣＤも共に辺長２の正三角形なので、三平方の定理より

●　△ＡＢＭは辺長の正三角形。
●　ＢＭ' ＝ ４
３

であることが判明します。

次の図は、△ＡＢＭ'を面に垂直な方向から見たものです。

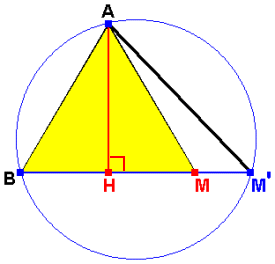
ＡよりＢＭ'に垂線を下ろし、その足をＨとすると、

●　ＡＨ ＝ ×
２		 ＝ ３
２
●　ＨＭ' ＝ ＢＭ' ー ＢＨ ＝ ４
３		 ー
２		 ＝ ５
６

よって、三平方の定理より

(ＡＭ')2 ＝ (ＡＨ)2 ＋ (ＨＭ')2 ＝ ( ３
２		 )2 ＋ ( ５
６		 )2 ＝ １３
３

∴　ＡＭ' ＝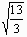

そこで、△ＡＢＭ'の外接円の半径をＲとすると、正弦定理より、

ＡＭ'
sin(∠Ｂ)		 ＝ ＡＭ'
sin６０°		 ＝
２
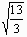
＝ ２
３		 ＝ ２Ｒ

∴　Ｒ ＝
３

ところで、△ＡＢＭ'の外接円は、明らかに四面体ＡＢＣＤの外接球の中心を通る円です。
ですから、求める球の半径はＲに等しく
３		 になります。

証明は終わりです。

◆宮城県　甘泉法師 さんからの解答。

ｘｙｚ座標上に題意を満たすように点をとる。
C=(0，0，1) D=(0，0，−1) A=(，0，0) B=(
2		 ， 3
2		，0)

座標を球の方程式 (x−a)2 ＋ (y−b)2 ＋(z−c)2 = r2 に代入すると

Ｃ：a2 ＋ b2 ＋ (1−c)2 = r2
Ｄ：a2 ＋ b2 ＋ (1＋c)2 = r2

よってc=0， r2 − a2 − b2 = 1

Ａ：(−a)2 ＋ b2 = r2

よって 3 − 2*a =1

a=
3
r2 − b2 = 4
3
Ｂ：(
2		 −a) 2 ＋ ( 3
2		 −b) 2 = r2
よって 1
12		 ＋ 9
4		− 3b = 4
3
b= 1
3
よって r=
3
答え　
3

　『球面に内接する四面体』へ

　数学の部屋へもどる