◆宮城県 アンパンマン さんからの解答。
【問題1】
Pac(5)=7
【問題2】
P(n)=Pac(n)を定義します。
問題のヒントより
P(n)
| =P(n-1)+{ | n-1 Σ k=1 | P(k)P(n-k)+ω(n;2)P([ | n 2 | ])}/2 | +{ | n-2 Σ j=1 | n-1-j Σ k=1 | P(j)P(k)P(n-j-k)+3 | [(n-1)/2] Σ j=1 | P(j)P(n-2j)+2ω(n;3)P([ | n 3 | ])}/6 |
ここでω(n;m)は
ω(n;m)= 1, m | n
= 0, そのほか。
この漸化式より、An(t)で表すと
An(t)-1
| =tAn-1(t)+ | [An-1(t)-1]2+An-1(t2)-1 2 | + | (An-1(t)-1)3+3(An-1(t2)-1)(An-1(t)-1)+2(An-1(t3)-1) 6 | mod tn+1 |
式を整理すると
An(t)-1
| =(t-1)An-1(t)+ | An-1(t)3 6 | + | An-1(t2) An-1(t) 2 | + | An-1(t3) 3 | mod tn+1 |
◆出題者のコメント。
解答ありがとうございます。
導出方法は正解ですが、ちょっとしたケアレスミスがあり、結果は両問題とも違います。
◆宮城県 アンパンマン さんからの解答。
【問題2】
問題のヒントより
P(n)
| =P(n-1)+{ | n-2 Σ k=1 | P(k)P(n-1-k)+ω(n-1;2)P([ | n-1 2 | ])}/2 | +{ | n-3 Σ j=1 | n-2-j Σ k=1 | P(j)P(k)P(n-1-j-k)+3 | [(n-2)/2] Σ j=1 | P(j)P(n-1-2j)+2ω(n-1;3)P([ | n-1 3 | ])}/6 |
この漸化式より、An(t) と An-1(t) で表すと
An(t)-1
| =tAn-1(t)+ | t{[An-1(t)-1]2+An-1(t2)-1} 2 | + | t{(An-1(t)-1)3+3(An-1(t2)-1)(An-1(t)-1)+2(An-1(t3)-1)} 6 | mod tn+1 |
式を整理すると
An(t)-1
| = | t(An-1(t))3 6 | + | tAn-1(t2) An-1(t) 2 |
+ | tAn-1(t3) 3 |
mod tn+1 |
◆出題者のコメント。
解答有難うございます。正解です。
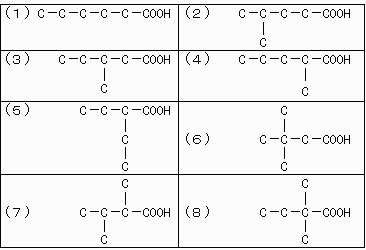
【問題1】の解答
N=5の場合の8種類(の異性体の構造式)を下表に示します

なお、問題2の式は 側鎖が0個の場合も含めて
| An(t)3 3! |
をベースに、そのうち2個が同型の場合の足りない分 |
| (6-3) | An(t2) An(t) 3! |
と、さらに3個とも同型の場合の足りない分 |
| (6-1-(6-3)) | An(t3) 3! |
、を足すことで |
| An+1(t)−1 t | を得られます。 |
【おまけ1】の解答
t=100とし、64bitの整数演算をオバーフローに注意しながら8組繰り返すと下記の結果が得られ、
Pac(8)=89まで分かります。
つまり、無限桁の整数演算ができて、tに適当に大きな数を使えばNのオーダーで可能です。
?11893917080402010101