 丂
丂廬偭偰丄儁儖偺曽掱幃偵偍偗傞儔僌儔儞僕儏偺傾儖僑儕僘儉偺庤朄偑揔梡壜擻偱偁傞丅
亂弨旛侾亃
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎丅
憡壛暯嬒偲憡忔暯嬒偺娭學幃偐傜丄
k=a2+b2-a*b*c
c=k+1
傑偨丄b亜a亞1丂偲偟偰傕堦斒惈偼幐傢傟側偄丅
0亙k亙c
| k= | a2+b2-a*b a*b+1 |
a,b,c偺慟壔幃傪尒偮偗傑偟偨丅
寢嬊丄 k=n2丂偲側傞丅
丂OPTION BASE 0
丂DIM C(10)
丂DIM A(10)
丂DIM B(10)
丂FOR K=1 TO 10
丂 LET C(K)=K^2+1
丂NEXT K
丂FOR K=1 TO 10
丂 PRINT K;"^2=";K^2
丂PRINT " C=";C(K)
丂 FOR J=1 TO 5
丂 IF J=1 THEN
丂 LET A(J)=K
丂 LET B(J)=A(J)*C(K)-A(J-1)
丂 PRINT USING "#############":A(J);
丂 PRINT USING "#############":B(J)
丂 ELSE
丂 LET A(J)=A(J-1)*C(K)-A(J-2)
丂LET B(J)=A(J)*C(K)-A(J-1)
丂PRINT USING "#############":A(J);
丂PRINT USING "#############":B(J)
丂END IF
丂NEXT J
丂 PRINT
丂NEXT K
丂END
1 ^2= 1
C= 2
1 2
2 3
3 4
4 5
5 6
2 ^2= 4
C= 5
2 10
10 48
48 230
230 1102
1102 5280
3 ^2= 9
C= 10
3 30
30 297
297 2940
2940 29103
29103 288090
4 ^2= 16
C= 17
4 68
68 1152
1152 19516
19516 330620
330620 5601024
5 ^2= 25
C= 26
5 130
130 3375
3375 87620
87620 2274745
2274745 59055750
6 ^2= 36
C= 37
6 222
222 8208
8208 303474
303474 11220330
11220330 414848736
7 ^2= 49
C= 50
7 350
350 17493
17493 874300
874300 43697507
43697507 2184001050
8 ^2= 64
C= 65
8 520
520 33792
33792 2195960
2195960 142703608
142703608 9273538560
9 ^2= 81
C= 82
9 738
738 60507
60507 4960836
4960836 406728045
406728045 33346738854
10 ^2= 100
C= 101
10 1010
1010 102000
102000 10300990
10300990 1040297990
1040297990 105059796000
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎丅
DIM C(10)
DIM A(0 TO 10)
DIM B(10)
FOR K=1 TO 10
LET C(K)=K^2+1
NEXT K
FOR K=1 TO 10
PRINT " K=";STR$(K)&"^2="&STR$(K^2)
PRINT " C="&STR$(C(K))
PRINT
FOR J=1 TO 5
IF J=1 THEN
LET A(J)=K
LET B(J)=A(J)*C(K)-A(J-1)
PRINT " A="&STR$(A(J));
PRINT " B="&STR$(B(J))
ELSE
LET A(J)=A(J-1)*C(K)-A(J-2)
LET B(J)=A(J)*C(K)-A(J-1)
PRINT " A="&STR$(A(J));
PRINT " B="&STR$(B(J))
END IF
NEXT J
PRINT " ................................."
PRINT " ................................."
PRINT "-----------------------------------------------------------------"
PRINT
NEXT K
END
弌椡
K=1^2=1
C=2
A=1 B=2
A=2 B=3
A=3 B=4
A=4 B=5
A=5 B=6
.................................
.................................
K=2^2=4
C=5
A=2 B=10
A=10 B=48
A=48 B=230
A=230 B=1102
A=1102 B=5280
.................................
.................................
K=3^2=9
C=10
A=3 B=30
A=30 B=297
A=297 B=2940
A=2940 B=29103
A=29103 B=288090
.................................
.................................
K=4^2=16
C=17
A=4 B=68
A=68 B=1152
A=1152 B=19516
A=19516 B=330620
A=330620 B=5601024
.................................
.................................
K=5^2=25
C=26
A=5 B=130
A=130 B=3375
A=3375 B=87620
A=87620 B=2274745
A=2274745 B=59055750
.................................
.................................
K=6^2=36
C=37
A=6 B=222
A=222 B=8208
A=8208 B=303474
A=303474 B=11220330
A=11220330 B=414848736
.................................
.................................
K=7^2=49
C=50
A=7 B=350
A=350 B=17493
A=17493 B=874300
A=874300 B=43697507
A=43697507 B=2184001050
.................................
.................................
K=8^2=64
C=65
A=8 B=520
A=520 B=33792
A=33792 B=2195960
A=2195960 B=142703608
A=142703608 B=9273538560
.................................
.................................
K=9^2=81
C=82
A=9 B=738
A=738 B=60507
A=60507 B=4960836
A=4960836 B=406728045
A=406728045 B=33346738854
.................................
.................................
K=10^2=100
C=101
A=10 B=1010
A=1010 B=102000
A=102000 B=10300990
A=10300990 B=1040297990
A=1040297990 B=105059796000
.................................
.................................
仧搶嫗搒丂摗杮 偝傫偐傜偺夝摎丅
徹柧偱偼偁傝傑偣傫
0 亙 a2 + b2 - abc 亙 c丂丂乧丂(1)
傪枮偨偡帺慠悢 a,b,c 偵偮偄偰
c 亞 2丂偑丂惉傝棫偮
傑偨丂娙扨偺偨傔丂a 亙 b 偲偡傞丅
乮丂a = b 偺偲偒丂a2 + b2 - abc = (2 - c)a2 亝 0 偲側傝(1)偵斀偡傞乯
鶣乯a = 1 偺偲偒
擟堄偺丂b ( 亜 1 : 帺慠悢) 偵偮偄偰
c = b 偲偡傞偲
a2 + b2 - abc = 1 + b2 -b2 = 1
鶤) a 亜 1 偺偲偒
a,b 偑屳偄偵慺側傜偽
a2 + b2 - abc = 1
偑惉傝棫偮偙偲偑梊憐偝傟傞丅乧丂乮仏乯
椺偊偽
丒b = a + 1 偺偲偒
c = 2 偲偡傞偲
丂a2 + b2 - abc
= a2 + (a + 1)2 - 2a(a + 1)
= a2 + a2 + 2a + 1 - 2a2 - 2a
= 1亙c
丒b = a2 - 1 偺偲偒
c = a 偲偡傞偲
丂a2 + b2 - abc
= a2 + (a2 + 1)2 - a2*(a2 - 1)
= a2 + a4 + 2a2 + 1 - a4 + a2
= 1 亙c
乮仏乯徹柧偼偱偒偰偄傑偣傫
僆僀儔乕偺掕棟乮僼僃儖儅乕偺彫掕棟乯偁偨傝傪巊偊偽丂晹暘揑偵徹柧偼偱偒傞偺偱偡偑丅丅丅
側偍丄峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎 偼
忋婰傪枮偨偡a,b,c 偲丂n2 亙 c 傪枮偨偡 n 傪巊偄
a'= na丆 b' = nb丆 c' = c 偲偟偨偲偒偺丂a',b',c' 偺慻崌傢偣偲巚傢傟傑偡
偙偺偲偒
丂a'2 + b'2 - a'b'c'
= n2*a2 + n2*b2 - n2*abc
= n2*(a2 + b2 - abc)
= n2
仧搶嫗搒丂愄偲偭偨媙暱 偝傫偐傜偺夝摎丅
忦審傪枮偨偡(a,b,c) 偺応崌偵丄
a2+b2-cab 偑庢傝偆傞抣偼丄1埲忋 c埲壓偱丄壗偐惍悢偺俀忔偵側偭偰偄傞儌僲偩偗偱偡丅
亂徹柧亃
f(a,b;c) = a2+b2-cab 偲抲偔帠偵偟傑偡丅
忦審偼丄丂0亙 f(a,b;c) 亝 c 側偺偱
c=1 偺応崌偼丄
f(a,b;c) = x 偲偡傞偲
x 偺忦審偑 1埲壓丄1埲忋 側偺偱 1 偟偐桳傝摼側偄偱偡偟丄
傑偨幚嵺丄(a,b) = (1,1) 偱丄f(a,b;c) = 1 偲偡傞帠偑偱偒傑偡丅
c=2 偺応崌偼丄
f(a,b;c) = x 偲丄側偭偨偲偡傞偲丄
x = (a-b)2 偱丄壗偐偺俀忔偱側偄偲丄偄偗傑偣傫丅
偦偺忋丄忦審偱們(=2) 埲壓丄1 埲忋丄偲偝傟偰偄傞偺偱丄
偁傞偲偡傟偽丄x=1 乮=12 ) 偟偐偁傝偊傑偣傫丅
傑偨幚嵺丄(a,b) = (2,1) 偱 f(a,b,c) = 1 偲偱偒傑偡丅
師偵丄c亞3 偺応崌偱偡偑丄
懳徧惈偐傜丄a亞b 偺斖埻偩偗傪峫偊傞帠偵偟偰丄
偝傜偵 f(a,b;c)亞0 偺忦審偐傜丄
a2-cab+b2亞0
偮傑傝丄 a亞( c+(c2-4)0.5 )/2 * b 偺斖埻偩偗傪峫偊傑偡丅
埲壓偱偼丄r = (c+(c2-4)0.5)/2 偲彂偔帠偵偟傑偡丅
r偼柍棟悢側偺偱丄0偱側偗傟偽丄偪傚偆偳 a = rb 偲側傞帠偼偁傝傑偣傫丅
傕偟丄a(1) 亜 r b(1) 傪枮偨偡帺慠悢偱丄
f(a(1),b(1);c) = x 偲側偭偨偲偟傑偡丅
偙偙偱丄師偺悢楍傪峫偊傑偡丅
(偨傇傫丄惔愳堢抝偝傫偺尵偆乽慟壔幃乿偱偼側偄偱偟傚偆偐丠)
a(n) = b(n-1)
b(n) = -a(n-1) + c * b(n-1)
偙偺悢楍偵偼丄師偺傛偆側摿挜偑偁傝傑偡丅
仸1: f(a(n),b(n);c) = f(a(n-1),b(n-1);c)
仸2: a(n) 亜 r b(n)
仸3: a(n-1)亜0 側傜偽丄a(n) 亙 a(n-1)
佹1丗
a(n)2 + b(n)2 - ca(n)b(n) = b(n-1)2 + a(n-1)2 - 2ca(n-1)b(n-1) + c2 b(n-1)2 + c b(n-1)a(n-1) - c2 b(n-1)2 = a(n-1)2 + b(n-1)2 - ca(n-1)b(n-1)佹2丗
a(n) - r b(n)
= b(n-1) + ra(n-1) - cr b(n-1)
> (r2 - cr + 1 ) b(n-1)丂
丂(婣擺朄壖掕偱丄a(n-1) 亜 r b(n-1) 偩偐傜丅)
= 0 (r 偺掕媊傛傝丅)
佹3丗
a(n) = b(n-1) 亙 1/r * a(n-1)
倰亜2 側偺偱丄a(n-1)亜0 側傜偽丄a(n)亙a(n-1) 偲側傝傑偡丅
a(n) 偼惍悢偺悢楍偩偐傜丄尭彮偡傞帪偼丄1 埲忋尭彮偟偰偄偔偺偱丄壗偐 惍悢 N 偑偁偭偰丄
a(N)亞1丄a(N+1)亝0 偲側傞偼偢偱偡丅
悢楍偺掕媊傛傝丄a(N+1) = b(N) 偱偁傞偺偱丄
寢嬊丄a(N)亞1 丄b(N)亝0 偲偄偆惍悢偑偁偭偰丄
f(a(N),b(N);c) = ... = f(a(1),b(1);c) = x 偲彂偗傞帠偵側傝傑偡丅
偮傑傝丄u = a(N) , v = -b(N) 偲抲偔偲丄
u亞1丄v亞0 側惍悢偱丄
u2 + v2 + cuv = x 偲彂偗傞帠偵側傞偺偱偡偑丄
偲偙傠偑丄v亞1 偩偲偡傞偲丄
x 亝 2 + c 偲側傝丄x 偑 c 埲壓偲偄偆忦審傪枮偨偟傑偣傫丅
偟偨偑偭偰丄v = 0 偲側傝丄
u 偼 1埲忋偱丄偁傞偲偡傟偽丄x = u2 偲彂偗偰丄偟偐傕 c 埲壓側儌僲偟偐桳傝摼傑偣傫丅
傑偨丄幚嵺丄u傪1埲忋偲偟偰丄(a,b) = (cu,u) 偲抲偔偲丄
f(a,b;c) = (cu)2 + u2 -c(cu)u = u2 偲偡傞帠偑偱偒傑偡丅
偲丄尵偆傢偗偱丄帺慠悢c 偵懳偟偰丄f(a,b;c) 偑庢傝摼傞抣偼丄1埲忋們埲壓偺丄壗偐偺俀忔偵側偭偰偄傞悢偲側傝傑偡丅
亂僐儊儞僩亃
壗偐偵庢傝溸偐傟偨傛偆偵丄偙偙偢偭偲丄1儢寧傎偳丄夝偗側偄側偀丄偲擸傫偱偄偨偺偱偡偑丄
c=3丄a=-10乣20丂b=-10乣20 偺 a2+b2-cab 傪昞偵偟偨帪偵丄傛偆傗偔婥偑晅偒傑偟偨丅
儅僀僫僗偺晹暘偺曽偑丄戝帠側傫偱偡偹丅
偙傫側僉儗僀側娭學偩偲丄壗偐堄枴偑偁傞傛偆側婥傕偡傞偺偱偡偑乧丅
偦傟偵偟偰傕丄帺慠悢偱丄a2+b2-cab 偑丄2 偵側傜側偄偺偼丄壗偐晄巚媍偱偡丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎
亂夝摎亃丂慡偰偺暯曽悢
佹N亖倎俀亄倐俀亅倎倐們 偲偍偔丅
們亖俀倣偺偲偒 N亖(倎亅倣倐)俀亅(倣俀亅侾)倐俀偱偁傝丄
(倣俀亅侾)偼暯曽悢偱偼側偄偺偱丄偄傢備傞堦斒壔偝傟偨儁儖偺晄掕曽掱幃偱偁傞丅
N亖侾偺応崌偼儁儖偺曽掱幃偱偁傝丄
偙偺応崌帺柧偱側偄夝丂(倎亅倣倐)亖倣 倐亖侾偑偁傞偺偱丄惍悢夝偼柍尷偵懚嵼偡傞丅
傑偨丂(倎亅倣倐)亖倣倐 偲偡傞偙偲偵傛傝丄N亖倐俀偲偱偒傞偺偱丄N偲偟偰擟堄偺暯曽悢偑懚嵼偡傞丅
幚嵺丄們 偺嬼婏惈偵傛傜偢丂
X侾亖侾 丆X俀亖們丆X値亄侾亖們*X値亅X値亅侾傪寁嶼偟丄
d俀亙們丂偵懳偟偰
倎亖d*X値亄侾丆倐亖d*X値偲偡傟偽丂
侽亙N亖d俀亙們丂偱偁傞丅丂
師偵N亗暯曽悢偺応崌傪峫偊傞丅
偙偺応崌丄倃亖倎乛倐丆兠亖N乛倐俀丂偲偡傞偲偒壓婰偱偁傞丅
倃俀亅們倃亄侾亖兠丂
兠仺侽偺丂夝丂倃亜侾偼丂壓婰偺傛偆偵廃婜俀偺楢暘悢昞尰乮倃偺桳棟悢嬤帡乯偑偱偒傞丅
 丂
丂
廬偭偰丄儁儖偺曽掱幃偵偍偗傞儔僌儔儞僕儏偺傾儖僑儕僘儉偺庤朄偑揔梡壜擻偱偁傞丅
亂弨旛侾亃
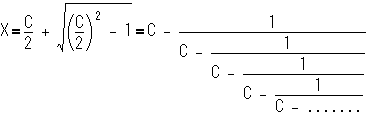
侽亙倎俀亄倐俀亅倎倐們亙們丂傪丂們丂偵娭偟偰彂偒捈偡偲
| 亅亅亅亅乮侾乯 |
倐亖侾丂倎亞俀偺帪丂們偼乮侾乯幃塃曈傛傝丂倎埲壓偱丄嵍曈傛傝倎亅侾傛傝戝偒偔柍偗傟偽側傜偢懄偪們亖倎偱偁傞丅
偙傟傪戙擖偡傞偲丂倎俀亄倐俀亅倎倐們亖侾亙們丂偱偁傞丅
傛偭偰偙偺応崌丄倎俀亄倐俀亅倎倐們偼侾偱偁傝丄暯曽悢偱偁傞丅
側偍丄們亖俀偺帪偄偢傟偵偟偰傕摼傜傟傞抣偼侾偱偁傞偑丄倎亖倐亄侾丂偱惉棫偡傞丅
傛偭偰埲崀丂倎亜倐亞俀丂們亞俁丂偱峫偊傞丅
偙偺偲偒
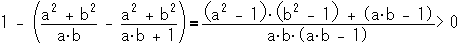 |
亅亅亅亅亅乮俀乯 |
乮俀乯幃傛傝丂倐乛倎亙侾偱偁傞偐傜丄
倎亜倐乮們亅侾乯丂丂丂丂丂丂丂丂丂亅亅亅亅亅乮俁乯
亂弨旛俀亃
N傪彂偒姺偊傞偲壓婰偱偁傞丅
偙偙偱丂N亖(倎亅兛倐)(倎亅兝倐)丂偱偁傞丅
傛偭偰丂俻亖倎乛倐 亜侾丂偲偡傞偲偒
忦審丂N亝們亅侾丂偲丂幃乮俁乯傛傝俻亞們亅侾丂傪戙擖偡傞偲
們亞俁側偺偱丂壓婰偱偁傞丅
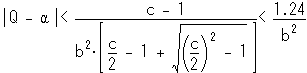 |
丂亅亅亅亅亅乮係乯 |
侾亖(倎亅兛倐)(倎亅兝倐)偺応崌偼
悢楍丂倃侾亖侾丆倃俀亖們丆倃俁亖們俀亅侾丂丒丒丒丒丒丒偺楢懕俀崁傪倎丆倐 偲偟偰梡偄傟偽惉棫偡傞偙偲傪慜偵帵偟偨丅
偄傑丄丂N亖(倎亅兛倐)(倎亅兝倐)偑惉棫偡傞屳偄偵慺側丂倎丆倐丂偑懚嵼偟偨偲偡傞丅
偙偺帪丂
N亖(倎亅兛倐)(倎亅兝倐) (倃値亄侾亅兛倃値)(倃値亄侾亅兝倃値)
亖(倎乫亅兛倐乫)(倎乫亅兝倐乫)
偙偙偱
倎乫亖倎*倃値亄侾亅倐*倃値*兛兝
亖倎*倃値亄侾亅倐*倃値
倐乫亖倎*倃値亄倐*倃値亄侾亅倐*倃値*乮兛亄兝乯
亖倎*倃値亄倐*倃値亄侾亅倐*倃値*們
偱偁傞丅
懄偪丄倎丆倐丂偑懚嵼偟偨偲偡傞偲丂N亖侾偺応崌偲摨偠枾搙偱柍尷偵懚嵼偡傞丅
偝傜偵丂N亖(倎亅兛倐)(倎亅兝倐)丂傪丂倎丆倐丂傪曄悢偲偡傞憃嬋慄偲峫偊傞偲丄
楢懕惈偐傜偦偺憃嬋慄忋偺揰楍丂乮併(N)*倃値亄侾 ,併(N)*倃値乯丂偺娫偵侾屄偢偮懚嵼偟偰偄傞偙偲偑傢偐傞丅
傛偭偰丄N偑旕暯曽悢側傜偽丄倐乫丂偲偟偰丂併N偐傜們併N丂偺暵嬫娫偺抣偺傕偺偱丂
N亖(倎亅兛倐)(倎亅兝倐)偲側傞傕偺偑懚嵼偡傞丅乮徻嵶偼嫵壢彂偵忳傞乯
亂寢榑亃
弨旛俀幃乮係乯傛傝丂偦偺傛偆側倐乫偵懳偟偰乥俻亅兛乥亙侾.俀係乛倐乫俀丂偱側偗傟偽側傜側偄丅
N亖侾偺応崌偺嬤帡抣丂俻亖們亅侾乛們丂偼乥俻亅兛乥乣侾乛們俁偱偁偭偰丄偙傟傪廫暘枮偨偟偰偄傞丅
倐乫亖丂倫們亄倯亙們併N丂偲偟偰丂俻亖們亅倫乛乮倫們亄倯乯偱丂俻傪嬤帡偟偨応崌傪峫偊傞丅
倯亖侽偵偍偄偰丂岆嵎偼丂乣侾乛們俀偱偁偭偨丅
倐乫亖丂倫們亄倯丂偲偡傞偙偲偵傛傝丄丂岆嵎偼丂乣倯乛倫們乮倫們亄倯乯丂曄壔偡傞丅
儀亅僗偺岆嵎偑乣侾乛們俁偱偁傞偺偱丄慡偰夵埆偲側傞偙偲偼柧傜偐偱偁傞偑丄
倯亖亇侾偱偁傟偽丂乣侾乛倫們乮倫們亄倯乯乣侾乛倐乫俀偱偁傝丄
N亗侾偺応崌偺壜擻惈偑巆傞丅丂
乷丂乣丗偺掱搙偺堄枴偱偡丅丂乸
幚嵺偵寁嶼偡傞偲丂倎亖們(倫們亇侾)亅倫 丂倐亖倫們亇侾丂偱偁傝丄
倎俀亄倐俀亅倎倐們亖倫俀亄侾亇倫們丂偱偁傞丅
倫亙併們偱偁傞偐傜丂倯亖亅侾偺偲偒丄丂倫俀亄侾亅倫們亙們乮侾亅倫乯亄侾丂偱偁傝丄
彮側偔偲傕丂倫亖侾偱側偄偲晧偱偁傞丅
倫亖侾偺偲偒丂俀亅們亙侽丂偱偁傞偺偱傗偼傝晧偱偁傞丅
傛偭偰丂倯亗亅侾偱偁傞丅
倯亖侾偺偲偒丂倫亞侾側偺偱
倫俀亄侾亄倫們亞俀亄們亜們丂偱偁傞丅
傛偭偰 N亜們丂偱偁偭偰忦審傪枮懌偟側偄丅>
埲忋傛傝N丂偼丂倎丂,丂倐丂偑慺偺帪偼丂侾丂偺傒偱偁傞丅
偮傑傝丂N偼暯曽悢偺傒偱偁傞丅
亂俹俽亃
忋婰寢榑傛傝乥N乥亙們丂偲偟偨応崌丂偁傞偄偼丂N亝們亄俀丂偲偟偨応崌偼暯曽悢埲奜偑偁傞傛偆偱偡丅
旕忢偵娙扨側栤戣暥偱偁傞偺偵傕偐偐傢傜偢墱偺怺偄栤戣偱丄傑偨儁儖偺曽掱幃偵偍偗傞儔僌儔儞僕儏偺傾儖僑儕僘儉偺忦審
乮乥N乥亙們乛俀丂憡摉乯傪庒姳堩扙偟偰偄傞偲偙傠偑傂偹偭偰偁傝丄廫暘妝偟傑偣偰偄偨偩偒傑偟偨丅
俧俠俢乮倎丆倐乯亖侾丂偲偄偆忦審傪偮偗偨傎偆偑丄夝摎偑侾偵尷傜傟傞偺偱丄椙偄偐偲巚偄傑偡丅
側偍丄摍壙側栤戣偲偟偰丄師偺傛偆偵傕嶌傝曄偊傜傟傑偡偹丅
帺慠悢丂倎丆倐丂丂俧俠俢乮倎丆倐乯亖侾丂偑偁偭偰丄
倎俀亄倐俀 傪揔摉側惍悢們偱妱偭偨偲偒偺彜偺惍悢晹偑丂倎*倐丂偱偁傞偲偒丄忚梋偼侾偱偁傞丅