◆広島県 清川 育男さんからの解答。
法則1
4次の方陣を1つのブロックと考える。
8次の方陣は4次の方陣ブロックが4個あるとみなす。
N(4の倍数)次の方陣は4次の方陣ブロックがN/4×N/4個あると考える。
法則2
スワップ(置換)する地点は対角線上にある所とする。
その場所にある数をKとするとき、対象となる数は、N2+1−Kとなる。
法則3
4次の方陣の場合を例にとれば、図1のように仮にあてはめる。
図1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16図1をもとに法則2を説明する。
図2 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1 8次の方陣の場合。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 置換する所は、 1と64, 4と61, 5と60, 8と57,10と55 11と54,14と51,15と50,18と47,19と46 22と43,23と42,25と40,28と37,29と36 32と33、と置換する。 64 2 3 61 60 6 7 57 9 55 54 12 13 51 50 16 17 47 46 20 21 43 42 24 40 26 27 37 36 30 31 33 32 34 35 29 28 38 39 25 41 23 22 44 45 19 18 48 49 15 14 52 53 11 10 56 8 58 59 5 4 62 63 1と出来上がります。以上です。
【コメント】
実は自分の意図していた解答と少し違うのですがこちらの方がわかりやすいですね。
これだけの情報からここまで分析できるというのはいつもながら感心しています。
Nが4の倍数であれば、この方法でできるはずです。
小・中学生の人はもっと大きな魔方陣も作ってみてくださいね。
◆石川県 数学好き さんからの解答。
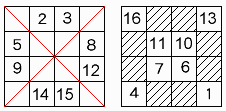
左図のように、左上から、1,2,3,4、
2行目に5,6,7,8といったように、順に数を入れていく。
ただし、対角線のところは入れない。
右図のように、左上から、16,15,14,13、
2行目に12,11,10,9といったように、順に数を入れていく。
ただし、今度は対角線のところだけに入れていく。

2つの図を重ね合わせると魔方陣ができる。
| 16 | 2 | 3 | 13 |
| 5 | 11 | 10 | 8 |
| 9 | 7 | 6 | 12 |
| 4 | 14 | 15 | 1 |
◆北海道の小学生 abe さんからの解答。
4の場合、1234
5678
9101112
13141516
1から16を当てはめて白いますは確定、黒いますは180度回転したところに入れます。
1■■4
■67■
■1011■
13■■16
白います(A)
□1514□
12□□9
8□□5
□32□
15から黒いますに入った数字をひいたもの(B)
AとBをかさねる
115144
12679
810115
133216
8*8のばあい、このようなカードを用意
□■■□□■■□
■□□■■□□■
■□□■■□□■
□■■□□■■□
□■■□□■■□
■□□■■□□■
■□□■■□□■
□■■□□■■□
1から64を順番に入れる。
黒いますは、65-ますの数字 を入れる
(例 45だったら65-45=20 20を上書き)
白いますは確定。
書くのが大変なので、書きません
N*Nのばあい、このカードをN*N/16枚用意する
□■■□
■□□■
■□□■
□■■□
1からN*Nまで順番にあてはめる。
白いますはそのまま確定。
黒いますは、N*N+1 から その数を引く。