 =0(A,Bは有理数)ならばA=B=0」
=0(A,Bは有理数)ならばA=B=0」◆埼玉県 \aleph_0 さんからの解答。
私の使っている大学の端末のエディタに数学記号やギリシャ文字を出す方法が分からないので、TeXの記号法を準用します。
(少々読みにくいかも知れません。)
また、次の記号を用います。
\Q=有理数体.
まず、一般に次の定理が成り立ちます。
定理1.1
p_1,...,p_nを相異なる素数、
\alpha_j=\sqrt{p_j} (j=1,...,n)とし、
L=\Q(\alpha_1,...,\alpha_n)とする。
このとき、
E=\{\alpha_1^{e_1}...\alpha_n^{e_n}|e_j=0,1 (j=1,...,n)\}
は、Lの\Q上の基底となる。
特に、[L:\Q]=2^n.
この定理より、題意のa,b,c,d,e\in\Qは存在しないことが直ちに分かるのですが、これを初等的な方法で解くのは結構大変だと思います。
それだけに、この問題に対する初等的な解法には興味があります。
【コメント】
わたしはTeXの記号を知らないので、そのまま載せました。
でも読める範囲で趣旨はよく分かります。
どなたか初等的な解法を見つけてください。
◆富山県 N.C さんからの解答。
定理0
「A+B =0(A,Bは有理数)ならばA=B=0」
=0(A,Bは有理数)ならばA=B=0」
(2の部分に、平方数でない任意の整数を代入しても同様。)
補題1
「A+B =
= を満たす有理数A,Bは存在しない」
を満たす有理数A,Bは存在しない」
(2の部分を5や15などで置き換えても同様な式が成り立つ。)
背理法で示す。
A+B =
= を満たす有理数の存在を仮定する.
を満たす有理数の存在を仮定する.
両辺を2乗して整理すると、
(A2+2B2-3)+2AB =0
=0
定理0よりAB=0となりA=0またはB=0
・A=0のときは、B =
= であり、両辺を
であり、両辺を 倍すれば、
倍すれば、
2B= となるが、これはBが有理数であることに反する.
となるが、これはBが有理数であることに反する.
・B=0のときは、A= となりこれはAが有理数であることに反する.
となりこれはAが有理数であることに反する.
いずれの場合も背理法の仮定に矛盾する.
定理1
「A+B +C
+C +D
+D =0(A,B,C,D有理数)ならばA=B=C=D=0」
=0(A,B,C,D有理数)ならばA=B=C=D=0」
A+B +C
+C +D
+D =0が成り立ったとすると
=0が成り立ったとすると
A+B =-(C+D
=-(C+D )
)
いま仮に「C+D が0」でないと仮定すると、(背理法の仮定)
が0」でないと仮定すると、(背理法の仮定)
両辺に-1/{C+D } を掛けて整理すると
} を掛けて整理すると
{(-AC+2BD)/(C2-2D2)}+{(AD-BC)/(C2-2D2)} =
=
となり、補題1に反するので、C+D =0
=0
従って、A+B =0,C+D
=0,C+D =0となるので、
=0となるので、
A=B=C=D=0
補題2
「A+B +C
+C +D
+D =
= を満たす有理数A,B,C,Dは存在しない」
を満たす有理数A,B,C,Dは存在しない」
背理法で示す.
もし、
A+B +C
+C +D
+D
= が成り立てば、
が成り立てば、
(A+B )+(C+D
)+(C+D )
)
=
の両辺を2乗して整理すると
(A+B )2+3(C+D
)2+3(C+D )2-5
)2-5
=-2(A+B )(C+D
)(C+D )
)
・(A+B )(C+D
)(C+D )≠0と仮定すると
)≠0と仮定すると
両辺を
-2(A+B )(C+D
)(C+D )で割ることができ、補題1に反する
)で割ることができ、補題1に反する
・(C+D )=0とすると補題1の3を5で置き換えた定理に反する.
)=0とすると補題1の3を5で置き換えた定理に反する.
・(A+B )=0とすると補題1の3を15で置き換えた定理に反する.
)=0とすると補題1の3を15で置き換えた定理に反する.
定理2
「A+B+C
+D
+E
+F
+G
+H
=0
(A,B,C,D,E,F,G,Hは有理数)ならば
A=B=C=D=E=F=G=H=0」
証明略。
(両辺を
{E+F +G
+G +H
+H }で割るのが面倒だから)
}で割るのが面倒だから)
補題3
「A+Bを満たす有理数A,B,C,D,E,F,G,Hは存在しない」+C
+D
+E
+F
+G
+H
=
証明略
ようやく準備ができました。いま、
 +a
+a +b
+b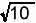
=c +d
+d +e
+e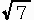
となる有理数があると仮定する.
ここで、仮に e≠0 であるとすると両辺をeで割って整理すれば、
(1/e) +(-c/e)
+(-c/e) +(-d/e)
+(-d/e) +(a/e)
+(a/e) +(b/e)
+(b/e)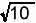
=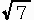
となり捕題3に反します.
一方、e=0 であるとすると、この式は定理2に反します.
多分もっと簡単な方法はあるのでしょうが、今は、
 ,
, ,
, ,
,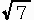 とそれらの積を含んでいるので、証明が4段階になっている方法しか思いつきません.
とそれらの積を含んでいるので、証明が4段階になっている方法しか思いつきません.
【出題者からのコメント】
実は肝心の
A+B +C +C +D +D ――――――――――――――― E+F  +G +G +H +H |
∈{P+Q +R +R +S +S | P,Q,R,S∈Q} | P,Q,R,S∈Q} |
部分を示すこと自体が一番の山場(本質)なのではないでしょうか?
直感的にはどう考えてもそうなるはず
(っていうか、Qを有理数体とするとき、 1, ,
, ,
, は
は
体Q( ,
, ,
, )=Q(
)=Q( ,
, )の基底になりうるので、結論自体は正しい)
)の基底になりうるので、結論自体は正しい)
なのですが、これを初等的に示すのは結構大変なんじゃないかなぁ??
実は、この部分が一番知りたかった所なので、省略しないで欲しかったです。
ただ、証明の流れ的には、この方向性以外には考えられないと思うので、『他にもっと簡単な方法』というのはおそらくないでしょう。
【出題者からのコメントの追加】
あっ!わかりました。
A+B +C +C +D +D ――――――――――――――― E+F  +G +G +H +H |
=I+J +K +K +L +L |
と置いて、分母を払って係数比較すればI,J,K,Lが求まるので、このような表示が可能なことが(初等的に)示されますね。
なるほど。これで、何の問題もないですね。
【出題者からのコメントの追加】
あっ、でも、厳密には係数比較した末に E,F,G,Hのすべてが0にならないとき
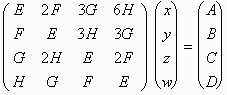
が解χ,y,z,wを持つかどうかにかかってくるわけですが、
(左辺の4次の行列をTとして、さらに右辺のベクトルを左辺の4次の行列の5列目に加えた4×5の拡大係数行列を~Tとします)
そのための必要十分条件は、rankT=rank~Tであり、この場合Tが正方行列なので
rankT=4を示す必要があります。
(すると自動的にrankT=rank~Tで、しかも解の一意性も示される)
これは、結局Tが正則であるということを示すことに他ならないのですが、これは決して明らかなことではないですね。
やっぱりこの手の問題は、無理矢理初等的にやろうとするには限界があるような気がしてきます(^^;)
◆石川県 平田 和弘 さんからの解答。
正しいかどうか自信がありませんがとりあえず考えました。
方針はやはりQを有理数として
有理数体Q( )={x(1)+y(1)
)={x(1)+y(1) |x(1),y(1)∈Q}を考えます。
|x(1),y(1)∈Q}を考えます。
Q( )は和・差・積・商について閉じている
)は和・差・積・商について閉じている
(要するに和・差・積・商もまたQ( )の要素となる)
)の要素となる)
ことを使用します。
題意をみたす有理数が存在するとして
x=a+b 、
、
y=c+d ,
,
z= とおくと
とおくと
x,y,z∈Q( )で、元の式は
)で、元の式は
z+ x
x
= y+e
y+e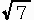 ・・・・・(A)となる。
・・・・・(A)となる。
z+ x-
x- y=e
y=e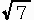
で両辺を2乗して
(z2+5・x2+3・y2-7・e2)/2
=w (∈Q( ) ・・・・(B)とおくと
) ・・・・(B)とおくと
w2+(15・x2・y2)-(3・z2・y2)-(5・z2・x2)
=2(wxy-xy・z2)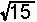 ・・・(C)
・・・(C)
となります。
ここでwxy-xy・z2≠0とすると、これで両辺を割ると
左辺∈Q( ) となり、
) となり、
右辺は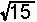 (not∈)Q(
(not∈)Q( ) なので矛盾
) なので矛盾
(※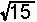 (not∈)Q(
(not∈)Q( )の証明は省略しました。
)の証明は省略しました。
簡単に証明はできますが・・・)
よってwxy-xy・z2=0 となり
ここでxy=0とすると、
1. x=0のとき、式(A)は
z= y+e
y+e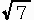 ・・・・(D)
・・・・(D)
となり、ey≠0とすると
(z2-3・y2-7・e2)/2ey=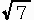 となり
となり
左辺∈Q( ) となり、
) となり、
右辺は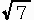 (not∈)Q(
(not∈)Q( ) なので矛盾
) なので矛盾
よってey=0となるが、このときe=0とすると
式(A)はz= y となり、
y となり、
y≠0とするとz/y= となり
となり
左辺∈Q( ) となり、
) となり、
右辺は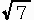 (not∈)Q(
(not∈)Q( ) なので矛盾
) なので矛盾
よってy=0となるが、このとき式(A)はz=0となり矛盾
y=0とすると式(A)はz=e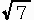 となり
となり
e≠0とすると、z/e=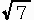 となり
となり
左辺∈Q( ) となり、
) となり、
右辺は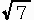 (not∈)Q(
(not∈)Q( ) なので矛盾
) なので矛盾
よってe=0となるが、このとき式(A)はz=0となり矛盾
2. 同様にy=0のときもすべて矛盾が導ける。
よってxy≠0 となりwxy-xy・z2=0の両辺をxyで割ると
w=z2=2 となる。
この結果を式(B)に代入して
(z2+5・x2+3・y2-7・e2)=4
よって、
x2=(2+7・e2-3・y2)/5・・・・・(E)
またw=z2=2を式(C)に代入すると、右辺=0なので、
4+(15・x2・y2)-(3・2・y2)-(5・2・x2)=0・・・(F)式(E)を式(F)に代入して整理すると
(3・y2-7・e2)(3y2-2)=0・・・(G)
となる。
(ア)3y2-2=0 のとき
y=c+d を代入して整理すると
を代入して整理すると
(3・c2+6・d2-2)+6cd =0 となるので
=0 となるので
3・c2+6d2-2・・・(H) かつ cd=0 となる
ア-1. c=0のとき
式(H)に代入してd2=1/3となるがこれを満たすd∈Qは存在しない。
ア-2. d=0のとき
式(H)に代入してc2=2/3となるがこれを満たすc∈Qは存在しない。
(イ)3・y2-7・e2=0 のとき
y=c+d を代入して整理すると
を代入して整理すると
(3・c2+6・d2-7・e2)+6cd =0 となるので
=0 となるので
3・c2+6・d2-7・e2=0・・・(I) かつ cd=0 となる
イ-1. c=0のとき
式(I)に代入して6・d2=7・e2となるが、
e≠0のとき、(d/e)2=7/6で、d/e=f∈Qとおくと
f2=7/6となるfは存在しない。
(※ここでeが有理数という条件と7と6が互いに素という条件が使用できた。)
よってe=0となるがこのとき式(I)は
3・c2+6・d2=0となるのでこれを満たすc,dは
c=d=0となりもとのy=0となる。
式(A)はz+ x=0となり、
x=0となり、
x≠0 とすると、-(z/x)= で
で
左辺∈Q( ) となり、
) となり、
右辺は (not∈)Q(
(not∈)Q( ) なので矛盾
) なので矛盾
よってx=0となるがこのときz=0となり矛盾
イ-2. d=0のとき
式(I)に代入して3・c2=7・e2となるが、
e≠0のとき、(c/e)2=7/3で、
c/e=g∈Qとおくとg2=7/3となるgは存在しない。
(※ここでもeが有理数という条件と7と3が互いに素という条件が使用できた。)
よってe=0となるがこのとき式(I)は
3・c2+6・d2=0となるのでこれを満たすc,dは
c=d=0となりもとのy=0となる。
式(A)はz+ x=0となり、
x=0となり、
x≠0 とすると、-(z/x)= で
で
左辺∈Q( ) となり、
) となり、
右辺は (not∈)Q(
(not∈)Q( ) なので矛盾
) なので矛盾
よってx=0となるがこのときz=0となり矛盾
以上より題意を満たす有理数は存在しない。
(感想)
どうもできたようでどこかに論理の飛躍があるような気がしますので間違いがありましたら指摘して下さい。
(補足証明)
上記中「d/e=f∈Qとおくとf2=7/6となるfは存在しない。」ことの証明
(「c/e=g∈Qとおくとg2=7/3となるfは存在しない。」ことの証明も同様)
もし存在したとすると、
f=n/m、(m,n)=1 となる整数m,nが存在する。
条件より、
6・n2=7・m2 ・・・(a)で、
(6,7)=1 より
n2=7s かつ m2=6t (s,tは任意の整数) なので
(a)に代入して、21s=21t よりs=t となる。
よってn・n=7s かつ m・m=3s となるが、元の条件より
(m,n)=1 ならば (m2,n2)=1 なので共通因数sをもつことに矛盾する。
◆富山県 N.C さんからの解答。
間違いがありましたので訂正させてください。
石川県の平田さんの解答を見てインスピレーションが沸きました.
ただし、Q( )が四則演算に閉じていることと、
)が四則演算に閉じていることと、
 ,
, などがQ(
などがQ( )に属さないことを使います.
)に属さないことを使います.
題意をみたす有理数が存在するとして
x=a+b 、y=c+d
、y=c+d とおくと
とおくと
x,y∈Q( )で、
)で、
元の式は
 +x
+x =y
=y +e
+e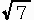 ・・・・・(A)となります。
・・・・・(A)となります。
これを
x -y
-y =-
=- +e
+e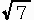
と変形して両辺2乗すると
5x2-2xy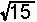 +3y2=2-2ze
+3y2=2-2ze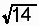 +7e2
+7e2
従って
{5x2+3y2-7e2-2}/2
=xy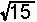 -e
-e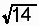 ・・・・・(B')
・・・・・(B')
ここで、
v={5x2+3y2-7e2-2}/2∈Q( )とおき、両辺2乗して
)とおき、両辺2乗して
v2-15x2y2-14e2
=-2xye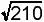 ・・・・・(C')
・・・・・(C')
・xye≠0 ならば、(C')式より
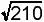
=-{v2-15x2y2-14e2}/{2xye}∈Q( )
)
となり、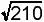 がQ(
がQ( )に属さないことに反します.
)に属さないことに反します.
・xy=0,e≠0ならば、(B')式より
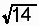 =-v/{e}∈Q(
=-v/{e}∈Q( )
)
となり、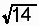 がQ(
がQ( )に属さないことに反します.
)に属さないことに反します.
・xy≠0,e=0ならば、(B')式より
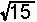 =v/{xy}∈Q(
=v/{xy}∈Q( )
)
となり、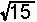 がQ(
がQ( )に属さないことに反します.
)に属さないことに反します.
・x=0,y≠0,e=0ならば(A)式より
 =
= /y
/y
となり がQ(
がQ( )に属さないことに反します.
)に属さないことに反します.
・x≠0,y=0,e=0ならば(A)式より
 =-
=- /x
/x
となり がQ(
がQ( )に属さないことに反します.
)に属さないことに反します.
・x=y=e=0ならば(A)式より =0となり、矛盾してしまいます.
=0となり、矛盾してしまいます.
以上、いずれの場合も矛盾が導かれるので、条件に当てはまるような有理数a,b,c,d,eは存在しません.
Q( )の知識を仮定するだけで、少し短くなりました.
)の知識を仮定するだけで、少し短くなりました.
【出題者からのコメント】
言葉数が足りなく、ちゃんと伝わらなかったみたいですみません。
えっと、N.C さんは『間違いがあったので訂正させて下さい』とありましたが、前回の解答での問題点は特にないと思います。
例の4元1次連立方程式に解があることは根性で示されるはず(たぶん。でなければ困る)なので、私は『決して明らかではない』と書きましたが、『明らかではないけれど、不可能ではない』というニュアンスが込められています。
(ただ、平田さんの解答もそうですが、N.C さんの今回の解答は、前回よりすっきりしていていいですね!)
また、『この手の問題は、初等的に限界がある』と書きましたが、“この問題”が初等的に無理であるという意味ではなくて(実際お二方が初等的に示されている!)“この手の”一般的な問題、つまり、ルートの個数がもっと増えた場合の見通しの悪さのことを言ったつもりでした。
なぜならば、 や
や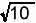 などの合成数の平方根の場合、
などの合成数の平方根の場合、 でくくり出すことによってルートの個数を減らすことに成功していますが、最終的に素数の平方根になった場合、これらのルートを解消する手段として、お二人の解答をざっと見る限りでは、両辺の2乗を使って個数を減らしているので、もっとルートの個数が増えた問題になると、この方法だけでは個数が減らないので、どうすればよいのか?ということになります。
でくくり出すことによってルートの個数を減らすことに成功していますが、最終的に素数の平方根になった場合、これらのルートを解消する手段として、お二人の解答をざっと見る限りでは、両辺の2乗を使って個数を減らしているので、もっとルートの個数が増えた問題になると、この方法だけでは個数が減らないので、どうすればよいのか?ということになります。
この問題を出した本当の意味は、この手の(一般化された)問題の場合、2乗してルートを減らせない難しさを堪能してもらいたかったところにあります。
ルートが4つまでだと、2乗する方法が使えるのですが、5つ以上になるとどうすればよいのか??というわけです。
合成数にしても難しさは変わらないだろうと思って安易に設定してしまったのですが………それが失敗でした(^^;;)
私が、本当ーーーに知りたかったのは一般化された場合のアイディアだったのです
お二方、(一般化された場合についての見通しについて)どう思われます??
なにかあれば、教えて下さい。
◆石川県 平田 和弘 さんからの解答。
●Asamiさんのコメントについて
1.
まず最初は全然違うことを考えていました。
ベクトルとか図形の性質を利用して解くのではないかと思いましたが、方針すら定まらず挫折しました。
2.
次にこの問題を見たとき、素数と合成数があることに気が付き、素数の性質を使って証明するのではないかと思いました。
それで両辺を素数と合成数に分けて考えたのですが計算が大変で、あえなく挫折しました。
素数の性質を使用するにはやはり根号をはずすしかなく、そのためには2乗することはやむをえない選択だと思います。
ただご指摘のように今回は合成数があったおかげで括り出しができ、計算が簡単にできただけだと思います。
\Aleph_0さん、N.C.さんの解答を見ましたが私の勉強不足の為、理解しにくいところがありました。
しかし、やはり計算の簡素化と省略を考えると(そうでないととても太刀打ちできない)有理数体ということを使用するしかなく、私の解答に至りました。
3.
代数学の本をみても、「素数の平方根は有理数Q上1次独立であることを証明せよ。」 などという問題しか載っていなくて、問題は実はこのことを言っているのかとも思いました。
この問題の根本的な解決には、やはり線形代数の理論を使うしか方法はないと思います。
根号の単純な計算は素数であればなかなか消えないので4つ位が限度(?)だと思います。
4.
従って、一般的に通用する方法の見通しは「初等的には」暗い(ない?)と思います。
5.
√の中が相異なる素数だけであれば、(数学的帰納法の使用が不得手なもので)以下のように順次考えればできるように思います。
(疑問・誤りがあれば指摘して下さい。)
|
(5-1).p(1),p(2)を相異なる素数とし、a(1),a(2)を有理数とし、
ならば a(1)=a(2)=0 |
の証明については
両辺を
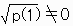 で割ると
で割ると
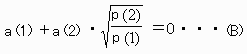
となりこの式の左辺をよくながめると、第1項が有理数なので、
a(2)≠0とすると第2項が√の中が平方数となるしかないが、それではp(1),p(2)が相異なる素数ということに矛盾する。
よってa(2)=0 となり、a(1)=0 が言えます。
同様に
(5-2).
| p(1),p(2),p(3)を相異なる素数とし、a(1),a(2),a(3)を有理数とし、
ならば a(1)=a(2)=a(3)=0 |
の証明については
両辺を
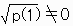 で割ると
で割ると
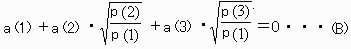
となりこの式の左辺をよくながめると、
◆石川県 平田 和弘 さんからの解答。
「3.に飛躍がありa(2),a(3)をそれぞれ2乗して同じ数になるかどうかの議論が抜けていて証明ができない。」 と思いましたが、次のようにすればできます。
もし同じになるとすると、
a(2)2・{(p(2)/p(1)}=a(3)2・{(p(3)/p(1)}より
a(2)2・{(p(2)}=a(3)2・{(p(3)}
よって
{a(2)/a(3)}2=p(3)/p(2) となり、
a(2)/a(3)も有利数となるので、これを改めて
n/m、(m,n)=1 とおくと
(n/m)2=p(3)/p(2) となります。
よって
n2・p(2)=m2・p(3)・・・(C)
ここで(p(2),p(3))=1 なので
n2=p(3)・u
m2=p(2)・v
u,vは整数
と書けますが、これらを(C)に代入して
u=v が得られます。この結果をみると、
n2=p(3)・u
m2=p(2)・u
となり、(m,n)=1 より
(m2,n2)=1 で共通因子uをもつことに矛盾する。
◆富山県 N.C さんからの解答。
A+B +C +C +D +D ――――――――――――――― E+F  +G +G +H +H |
∈{P+Q +R +R +S +S | P,Q,R,S∈Q} | P,Q,R,S∈Q} |
の証明についてのコメントです.
A+B ――――――――― E+F  |
∈{P+Q | P,Q∈Q} | P,Q∈Q} |
の証明は、
N=(E+F )(E-F
)(E-F )= E2- 2F2 とおくと、
)= E2- 2F2 とおくと、
これは有理数となって,
A+B ――――――――― E+F  | = | (A+B )(E-F )(E-F ) )――――――――――― N |
となることを使います.
同様に, と
と (とそれらの積)を含む場合ですが、
(とそれらの積)を含む場合ですが、
N=(E+Fとおけば、Nは有理数となります。+G
+H
)(E-F
+G
-H
)(E+F
-G
-H
)(E-F
-G
+H
)
従って,
(A+Bの計算は、+C
+D
)/(E+F
+G
+H
)
(A+Bの計算に帰着します。+C
+D
)(E-F
+G
-H
)(E+F
-G
-H
)(E-F
-G
+H
)/N
# 参考までに、 と
と と√5(とそれらの積)を含む場合は,上記のNに相当する式は「8次式」となり、さらに大変です。
と√5(とそれらの積)を含む場合は,上記のNに相当する式は「8次式」となり、さらに大変です。
以上から,計算力だけでこの問題を解決するのは不可能では無いにしても、膨大な計算量になることは確実です.
◆埼玉県 \aleph_0 さんからの解答。
出題者の方が、一般の場合について悩んでおられたので、少しコメントしたいと思います。
前回も述べたように、この問題は次の定理を示せば十分です。
定理2.1.
p_1,...,p_nを相異なる素数とし、
L=\Q(\sqrt{p_1},...,\sqrt{p_n})
とおく。このとき、
E=\{(\sqrt{p_1})^{e_1}...(\sqrt{p_n})^{e_n}|e_j=0,1 (j=1,...,n)\}
は、Lの\Q上の基底となる。
特に、[L:\Q]=2^n.
体論を駆使すれば、これはもっとsmartに証明できますが、以下のように初等的に示すこともできます。
まず、次の補題を準備します。
補題2.2.
p_1,...,p_nを相異なる素数とし、
L_j=\Q(\sqrt{p_1},...,\sqrt{p_j}) (j=0,1,...,n)
とおく。
ただし、L_0=\Qである。
このとき、次が成り立つ。
(a) E_n=\{1,\sqrt{p_n}\}は、L_nのL_{n-1}上の基底である。
(b) pをp_1,...,p_{n-1}と異なる素数とする。
このとき、0でない整数Nおよびx_{n-1}\in L_{n-1}に対して
(2.1) p=Nx_{n-1}^2
が成り立つならば、pはNを割り切る。
証明. nに関する帰納法により示す。
まずn=1ならば、(a),(b)ともに明らかである。
次にn>1とし、n-1に対しては(a),(b)ともに成り立つと仮定する。
まず(a)を示す。
a_{n-1},b_{n-1}\in L_{n-1}に対して
a_{n-1}+b_{n-1}\sqrt{p_n}=0
とおく。
今、b_{n-1}\ne 0と仮定すると、
(2.2) \sqrt{p_n}=-a_{n-1}/b_{n-1}\in L_{n-1}
であるから、帰納法の仮定(a)より、
あるa_{n-2},b_{n-2}\in L_{n-2}が存在して、
-a_{n-1}/b_{n-1}=a_{n-2}+b_{n-2}\sqrt{p_{n-1}}.
これを(2.2)に代入し、両辺を平方すると、
p_n=(a_{n-2}^2+p_{n-1}b_{n-2}^2)+2a_{n-2}b_{n-2}\sqrt{p_{n-1}}.
再び帰納法の仮定(a)より、次を得る。
(2.3a) p_n=a_{n-2}^2+p_{n-1}b_{n-2}^2,
(2.3b) 0=2a_{n-2}b_{n-2}.
(2.3b)より、a_{n-2}=0またはb_{n-2}=0であるが、
a_{n-2}=0ならば、(2.3a)より、p_n=p_{n-1}b_{n-2}^2となるから、
帰納法の仮定(b)より、p_nがp_{n-1}を割り切ることになり、
p_nとp_{n-1}が異なる素数であるという仮定に反する。
一方、b_{n-2}=0ならば、(2.3a)より、p_n=a_{n-2}^2となるから、
帰納法の仮定(b)より、p_nが1を割り切ることになり矛盾。
したがって、
b_{n-1}=0, a_{n-1}=-b{n-1}\sqrt{p_n}=0を得る。
L_n=L_{n-1}(\sqrt{p_n})より、
[L_n:L_{n-1}]\le 2であるから、(a)が成り立つ。
次に(b)を示す。
帰納法の仮定(a)より、あるx_{n-2},y_{n-2}\in L_{n-2}が存在して、
x_{n-1}=x_{n-2}+y_{n-2}\sqrt{p_{n-1}}.
これを(2.1)に代入すると、
p=N[(x_{n-2}^2+p_{n-1}y_{n-2}^2)+2x_{n-2}y_{n-2}\sqrt{p_{n-1}}].
再び帰納法の仮定(a)より、次を得る。
(2.4a) p=N(x_{n-2}^2+p_{n-1}y_{n-2}^2),
(2.4b) 0=2x_{n-2}y_{n-2}.
(2.4b)より、x_{n-2}=0またはy_{n-2}=0であるが、
x_{n-2}=0ならば、(2.4a)より、p=Np_{n-1}y_{n-2}^2となるから、
帰納法の仮定(b)より、pはNp_{n-1}を割り切る。
仮定より、pとp_{n-1}は互いに素であるから、pはNを割り切る。
一方、y_{n-2}=0ならば、(2.4a)より、
p=Nx_{n-2}^2となるから、帰納法の仮定(b)より、pはNを割り切る。
したがって、いずれの場合もpはNを割り切るから、(b)が成り立つ。
q.e.d.
この証明のポイントは、仮定(a)だけでなく仮定(b)を仮定することにあります。
仮定(a)だけでは、出題者の方がおっしゃっているように、n>4で論理が破綻します。
この補題の(a)および体の一般論より上の定理が従うことは明らかです。
【出題者からのコメント】
平田さん、N.Cさんをはじめ、皆さんのアイディアには驚かされてばかりです。
特に\aleph_0 さんありがとうございました。
巧妙な証明に感動しました。
ただ、証明途中で
![]()
を認めてしまってるような気がするのですが、これは、体Kにおいて
K(α1,………,αn)=K(α1,………αn-1)(αn)が成り立つという一般的事実から結果的に正しいのだけれども、初等的には、明らかなのでしょうか?
私の理解不足から来る愚問かもしれませんが、宜しくお願いします。
【出題者からのコメント】
あっ。わかりました。
体になるだの、基底だのと、余計なことを考えないで、単に、
![]() を
を
『A1,A2,………,A2n
(ただし各Aiは1,P1,……,Pnのいくつかを組み合わせたものの積の平方根で、組み合わせ2n通りすべてに渡らせたもの)
のQ上の結合で表されるものの全体』と定義しておけば問題ないのかな。
あっ。でも、やっぱり
-a_{n-1}/b_{n-1}\in L_{n-1}部分なのですが、
![]() を
を
『A1,A2,………,A2n
(ただし各Aiは1,P1,……,Pnのいくつかを組み合わせたものの積の平方根で、組み合わせ2n通りすべてに渡らせたもの)
のQ上の結合で表されるものの全体』と定義したものから出発した場合、
L_{n-1}が体であることを示す必要があると思います。
![]() の定義の段階で
の定義の段階で
![]() を含む最小の体と定義したものから出発すると、
を含む最小の体と定義したものから出発すると、
今度はK(α1,………,αn)=K(α1,………αn-1)(αn)が成り立つことを示さねばならないと思います。
初等的にどうなのでしょうか?
◆埼玉県 \aleph_0 さんからの解答。
出題者の方へ。
ご指摘の事実は、確かに無断で使わせて頂いていました。
言葉数が足りず余計に悩ませてしまい、申し訳ありませんでした。
"添加した体"については、ここでは次のように定義したいと思います。
定義3.1.
Kを体、ΩをKを含む体とし、α1,...,αn∈Ωとする。
このとき次のように定義する:
K(α1,...,αn)={f(α1,...,αn) | f(X1,...,Xn)∈K(X1,...,Xn)}
ただし、K(X1,...,Xn)はK上の有理式体である。
定義より、K(α1,...,αn)はK,α1,...,αnを含む最小の体である。
このとき、ご指摘の事実が成り立ちます。
命題3.1.
Kを体、ΩをKを含む体とし、α1,...,αn∈Ωとする。
このとき次が成り立つ。
K(α1,...,αn)=K(α1,...,αn-1)(αn).
これを示すには、次を示せば十分です。
命題3.2.
Kを体とする。このとき、K上の有理式体に関して次が成り立つ。
(3.1) K(X1,...,Xn)=K(X1,...,Xn-1)(Xn)
証明. まず、
K[X1,...,Xn]=K[X1,...,Xn-1][Xn]⊂ K(X1,...,Xn-1)[Xn]
であるから、両辺の商体を取って、
(3.2) K(X1,...,Xn)⊂ K(X1,...,Xn-1)(Xn).
一方、∀φ(Xn)∈K(X1,...,Xn-1)[Xn]に対して、
∃φi(X1,...,Xn-1)∈K(X1,...,Xn-1) (0≦i≦r)が存在して、
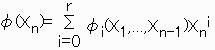
このとき(φiたちを"通分"することにより)、
∃fi(X1,...,Xn-1),g(X1,...,Xn-1)∈K[X1,...,Xn-1]が存在して、
φi(X1,...,Xn-1)=fi(X1,...,Xn-1)/g(X1,...,Xn-1).
ここで、
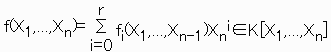
とおけば、
φ(Xn)=f(X1,...,Xn)/g(X1,...,Xn-1)∈K(X1,...,Xn).
したがって、
K(X1,...,Xn-1)[Xn]⊂ K(X1,...,Xn)
であるから、両辺の商体を取って、
(3.3) K(X1,...,Xn-1)(Xn)⊂ K(X1,...,Xn).
(3.2),(3.3)より、(3.1)が従う。 q.e.d.