◆滋賀県 ippei さんからの解答。
【問題1】
とりあえず、存在は示せます。
点pが正三角形の重心ならば、3つの線分からできる3角形は正三角形。
【問題2】
とりあえず、存在は示せます。
点pが正三角形の重心を通り平面に垂直な直線上にあれば、3つの線分からできる3角形は正三角形。
この問題は一般化するとおもしろい問題ですね。
◆富山県 N.C さんからの解答。
【問題1】について
●CASE1
点Pが正三角形の内部にある場合。
# 次の作業をすると見やすくなります。
# 三角形PABとPACを切り抜いておく。
2つの三角形PABとPACを移動して、辺ABとACを重ねます。
点Pの移動後の位置は、三角形PAB側をγ、PAC側をβとし、2点BとCが移動後に重なった点をαとします。
三角形Aβγは、Aβ=Aγ(ともにPAに等しい)で、
∠A=60度ですから正三角形です。
したがって、
PA=βγ、PB=γα、PC=αβとなり、
三角形αβγは求めるものになっています。
●CASE2
点Pが三角形の外部にあって、線分PAが辺BCと交わる場合
# 次の作業をすると見やすくなります。
# 三角形PABとPACを切り抜いておく。
2つの三角形PABとPACを移動して、辺ABとACを重ねます。
点Pの移動後の位置は、三角形PAB側をγ、PAC側をβとし、2点BとCが移動後に重なった点をαとします。
三角形Aβγは、Aβ=Aγ(ともにPAに等しい)で、
∠A=60度ですから正三角形です。
したがって、
PA=βγ、PB=γα、PC=αβとなり、
三角形αβγは求めるものになっています。
●CASE3
点Pが三角形の外部にあって、三角形PBCの内部に点Aがある場合
# 次の作業をすると見やすくなります。
# 三角形PABとPACを切り抜いておく。
2つの三角形PABとPACを移動して、辺ABとACを重ねます。
点Pの移動後の位置は、三角形PAB側をγ、PAC側をβとし、2点BとCが移動後に重なった点をαとします。
三角形Aβγは、Aβ=Aγ(ともにPAに等しい)で、
∠A=60度ですから正三角形です。
したがって、
PA=βγ、PB=γα、PC=αβとなり、
三角形αβγは求めるものになっています。
●CASE4
点Pが、辺BC上にある場合
これは(CASE1)や(CASE2)の特殊例となります。
●CASE5
点Pが、3つの頂点Aに重なる場合
辺の長さが0の三角形の存在を認めると、
これは(CASE1)や(CASE3)の特殊例となります。
長々と書きましたが、なんか一つにまとまらないものだろうか?
◆富山県 N.C さんからの解答。
【問題1】について
毎回、解答を送信したその翌日に、よりよい方法に気付くのはどうしてでしょうか。
(証明の背景にある原理は同じですが,記号が簡単になる。)
原理は同じなので,証明の基本方針だけ言えば、
まず、三角形PACを点Aを中心に60度回転して、
辺ACを辺ABに重ねることができることを示す。
次に,点Pの移動後の位置をP'とし、
三角形APP'が正三角形となることを示す。
最後に、三角形BPP'が求める三角形であることを示す。
(注:三角形PACがつぶれてしまう場合も、上の証明の流れは同じです。)
なお、前回の証明の場合分けに、
「点Pが三角形の外部にあって、辺ABの延長線上にある場合」
が、抜けておりました。
◆京都府 sambaGREEN さんからの解答。
【コメント】
できる場合できない場合の予想は殆どできていて,問題2の証明も問題1を前提にすでに出来ていました。
N.Cさんの解答を見せてもらったおかげで,問題2の解答を送ることが出来ました。
その前に少し問題1の補足をしておきます。
【問題1】
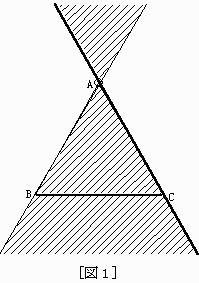
[図1]のような斜線領域に点Pがあるときを考えます。
(細線は含まない。太線は含む。点Aを除く)

(実際は,細線と一部を除くと,この領域以外でもN.Cさんの方法が使えますが,証明の都合上です)
N.Cさんの証明どおり,△PABを点Aのまわりに60°回転させることによって,
PA,PB,PCを三辺とする三角形の存在が示せます。
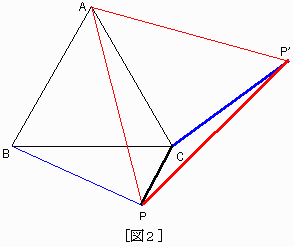
1例を[図2]に示しておきます。
PA・・赤,PB・・青,PC・・黒
[図1]の斜線部分を三角形ABCの重心の周りに
120°,240°回転させることにより,頂点A,B,C以外を埋め尽くせます。
ただし,[図2]でP,C,P'が一直線上になって三角形にならない場合があります。
∠ACP+∠ACP'=180° すなわち
∠ABP+∠ACP'=180°のときです。
このとき,A,B,C,Pが共円点になります。
[図3]に示しておきます。
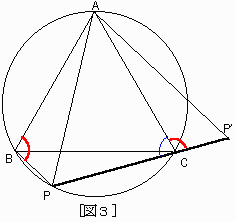
従って,
点Pが正三角形ABCの外接円の上にないとき,
PA,PB,PCを三辺とする三角形を作ることができる。
点Pが正三角形ABCの外接円上のとき,
PA,PB,PCを三辺とする三角形は作れない。
また,このとき
PA+PB=PC または
PB+PC=PA または
PC+PA=PB
【問題2】
平面π上にない点Pの平面πへの正射影を点Qとするとき,問題1の結果より,
QC≧QA+QB
(QC≧QA,QC≧QA)としても一般性を失わない。
直角三角形PQCと直角三角形PQAを[図4]のように重ねる。
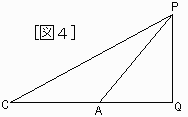
図から PC≧PA …(1)
PA+(QC−QA)≧PC …(2)
PC>QC…(3)
QA=0のときも,不等号は成り立つ。
QC=QAのとき等号成立
また,同様にして
PC≧PB …(4)
PB+(QC−QB)≧PC …(5)
QB=0のときも,不等号は成り立つ。
QC=QBのとき等号成立
(2)+(5)より,
PA+(QC−QA)+PB+(QC−QB)≧2PC PA+PB≧PC+(PC−QC)+(QA+QB−QC)>PCなぜならば,
従って,(1),(4)と,PA+PB>PCから,
PA,PB,PCを三辺とする三角形を作ることができる。
【蛇足】
[問題1][問題2]の結果をあわせると,正三角形ABCの外接円を除いて,すべての空間において,
PA,PB,PCを三辺とする三角形を作ることが出来る。