
―――
4
◆大阪府 CHECK さんからの解答。
題意の楕円は原点中心、半径1の円をx軸方向にa倍,y軸方向にb倍したものである。
∴原点中心、半径1の円内の図形の面積も同様に拡大される。
よって求める最大値は,原点中心、半径1の円の内接三角形の面積の最大値を
ab倍したものである。
点O中心半径1の円に内接する三角形の各頂点をA,B,Cとする。
まず点B,Cを固定すると,△ABCの面積が最大となるのは,点Aから直線BCに下ろした垂線の長さが最大となるときで,
それはAB=ACのときである。
∴△ABCは二等辺三角形である。
次に∠BOC=θ(0≦θ<360)とすると,正弦定理より
| BC= |
1 ― 2 | sin( |
θ ―― 2 | ), |
また点Aから線分BCに下ろした垂線の足をHとして
| AH=1+cos( |
θ ―― 2 | )となる。 |
| ∴△ABC= |
1 ―― 2 | ×BC×AH |
| = |
1 ―― 2 | sin( |
θ ―― 2 | ){1+cos( |
θ ―― 2 | )} |
これをf(θ)とすると導関数f'(θ)は
f'(θ)
| = |
1 ―― 2 | {cos( |
θ ―― 2 | )+cos2( |
θ ―― 2 | )−sin2( |
θ ―― 2 | )} |
| = |
1 ―― 2 | {2cos2( |
θ ―― 2 | )+cos( |
θ ―― 2 | )−1} |
| = |
1 ―― 2 | {2cos2( |
θ ―― 2 | )−1}{cos( |
θ ―― 2 | )+1} |
∴f'(θ)=0となるのはθ=120のとき。
このとき△ABCは正三角形であり,
| その面積は |
3 ――― 4 | 。 |
よって,求める最大値は
3 ab ab―――― 4 | である。 |
◆宮城県 アンパンマン さんからの解答。
任意点Pについて、三角形PQRの面積が最大になるような点Q,Rが存在する。
(最大の時はPと関係なく面積は同じ値です。)
面積が最大になるときは、楕円上の点P,Q,Rの接線
よってPを(-a,0), Qを(r,s), Rを(r,-s);
a,r,s≧0 とすると
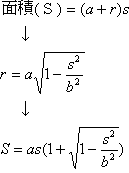
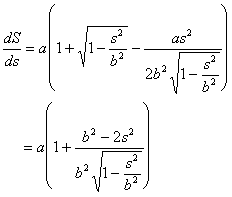
dS/ds=0
↓
b2(b2-s2)=(2s2-b2)2
↓
s= b /2
/2
↓
r=a/2
| 最大になるときの面積=(a+ |
a ― 2 | ) |
b ―――― 2 | = |
3 ab ab―――― 4 |