『２つの三角形』解答

◆東京都　Asami さんからの解答

【周の長さが最小になるような位置の決定】

周の長さはきっと簡単な数式で表せるのだとは思いますが、ここでは内部の△の位置の決定の仕方(ちょっと苦しいかも？)について書きます。

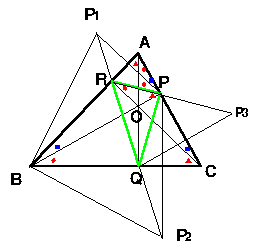
内部の△について、ＡＣ,ＣＢ,ＢＡ上にある頂点をそれぞれＰ,Ｑ,Ｒとします。
Ｐを固定したとき、△ＰＱＲの周の長さが最小となる位置は、ＰのＡＢ,ＢＣに関する対称点を
Ｐ1,Ｐ2としたときのＰ1Ｐ2の長さに対応します。

Ｐ1Ｐ2とＡＢ,ＢＣとの交点をＰ3,Ｐ4とすれば
Ｐ3Ｐ4の長さはＰ1Ｐ2の半分だから、
結局ＰからＡＢ,ＢＣへの垂線の足Ｐ3,Ｐ4を結んだ線分の長さについて(Ｐを動かしたとき)それが最小値をとるような、Ｐの位置を決定すれば良い。

∠Ａ＝a,∠Ｃ＝c,
∠Ｐ3ＰＰ4＝θ(＝a+b)
ＡＣ＝１,ＡＰ＝ｍとおけば、

 (Ｐ3Ｐ4)2
＝(m・sina)2＋((1-m)sinc)2−２(m・sina)((1-m)sinc)cosθ……★
このｍに関する２次関数の、区間[0,1]における最小値をとるようなｍを決定すれば、Ｐ,Ｑ,Ｒの位置が決まることになる。
★＝Ｋ{m−((sinc)2+cosθsinasinc)／((sina)2+(sinc)2+2cosθsinasinc)}2＋Ｌ
という形に書けるが、この軸は区間[0,1]内に収まっている。
(∵０≦sinc＋cosθsina
すなわち０≦sinc−cos(180−θ)sinaが成り立つことと同値であるが、右辺は
(ＡからＢＣへ下ろした垂線の長さ)−(ＡＢ上の任意の点からＢＣへ下ろした垂線)
を意味しているので確かに成立している)

また★の左辺を見れば分かるようにＬは正の値を取る。

つまり、

m＝(sinb)2+cosθsinasinc
―――――――――――――――
(sina)2+(sinc)2+2cosθsinasinc

となるような位置にＰを設定し、ＰからＡＢ,ＢＣへの対称点Ｐ1,Ｐ2を とり、線分Ｐ1Ｐ2のＡＢ,ＢＣへの交点をそれぞれＱ,Ｒにすればよい

◆埼玉県　斉藤　誠 さんからの解答

「光の反射で入射角と反射角は等しい」ことを考えると垂線に関係している。
また三角形の対称性から垂心に関係するのではないかと・・・
当たっていたようだ。

三角形の頂点Ａ，Ｂ，Ｃから対辺に引いた垂線の足をそれぞれＱＰＲとする。

ＢＣを直径としＰ、Ｒを通る円を、ＡＣを直径としＲ，Ｑを通る円等を考えると、円周角の関係などから、

△ＡＲＰ∽△ＱＲＢ∽△ＱＣＰが導かれます。

点ＰのＡＢ，ＢＣに関する対称点をＰ1、Ｐ2とすると
　∠ＡＲＰ1
＝∠ＡＲＰ（∵合同三角形）
＝∠ＱＲＢ（∵相似三角形）

同様に
∠ＣＱＰ2＝∠ＲＱＢ
となり、Ｐ1、Ｒ、Ｑ、Ｐ2は同一直線上にある。

おなじ論法でＲＰＰ3も同一線上になる。
よって、三角形ＱＰＲが周囲長最小になる。

Ｐ1Ｐ2の長さをＬとすると、
ＢＰ1＝ＢＰ2＝ＰＢなので余弦定理より

Ｌ2
＝２ＰＢ2（１−ｃｏｎ２Ｂ）
＝２ＰＢ2（１−（２ｃｏｓ2Ｂ−１））
＝４ＰＢ2（１−ｃｏｓ2Ｂ）
＝４ＰＢ2・ｓｉｎ2Ｂ

ＰＢは三角形の高さなので、三角形の面積をＳとすると
Ｌ2＝４×（２Ｓ）2
―――――――
ｂ2		×ｓｉｎ2Ｂ
＝４×（２Ｓ）2
―――――――
ｂ2		×（２Ｓ）2
――――――
（ａｃ）2
＝（８Ｓ2）2
―――――――
（ａｂｃ）2

Ｌ＝８Ｓ2
―――――――
ａｂｃ

面積Ｓを展開しまとめると

Ｌ=(ａ+ｂ+ｃ)(-ａ+ｂ+ｃ)(ａ-ｂ+ｃ)(ａ+ｂ-ｃ)
――――――――――――――――――――
２×ａｂｃ

垂心と内心が一致する図形は記憶にないなー。

◆東京都　Asami さんからのコメント

なるほど。垂心(線)が絡んでいたんですね。

私が計算した式に於いて、

ＡＰ：ＰＣ
＝(sinc)2+cosθsinasinc：(sina)2+cosθsinasinc
＝(sinc)2+cos(a+c)sinasinc：(sina)2+cos(a+c)sinasinc
＝(cosa)(sinc)(sinacosc＋cosasinc)：(sina)(cosc)(sinacosc＋cosasinc)
＝(cosa)(sinc)：(sina)(cosc)
＝１／tana：１／tanc
だから、確かにＰはＢからＡＣへ下ろした垂線の足になっていますね。

もっと(特殊な図形になっていないかどうかを)追求すべきでした。
垂線とは………気づかなかったなあ。
計算で強引にやっていくと、図形的(本質的)性質を見失うことがありますね。

◆宮城県　アンパンマン さんからの解答

辺BCをX、辺CAをY、辺ABをZ　とすると
三角形XYZの周の長さが最小値になる条件は

∠AZY=∠BZX, ∠BXZ=∠CXY, ∠CYX=∠AYZ

つまり
△AYZ ∽ △XBZ ∽ △XYC ∽ △ABC

AZ/AC=AY/AB =r (=YZ/BC) とおくと

BC
=BX+XC
=(BZ/BC)*AB+YC/BC*AC
=(AB-rAC)/BC*AB+(AC-rAB)/BC*AC

↓

r=(CA2+AB2-BC2)/(2CA*AB)

同様に

XY/AB=(BC2+CA2-AB2)/(2BC*CA)

ZX/CA=(AB2+BC2-CA2)/(2AB*BC) 

　三角形の周の長さの最小値
＝XY＋YZ＋ZX
＝AB*(BC2+CA2-AB2)/(2BC*CA)＋BC*(CA2+AB2-BC2)/(2CA*AB)＋CA*(AB2+BC2-CA2)/(2AB*BC)
＝[2(AB*BC)2+2(BC*CA)2+2(CA*AB)2-AB4-BC4-CA4]/(2AB*BC*CA)
＝8S2/(AB*BC*CA)
ここで　S=△ABCの面積。

　『２つの三角形』へ

　数学の部屋へもどる