◆東京都の中学校3年生 きぃ さんからの解答。
m<100の範囲では,
293/1028≒0.9904
2103/1031≒1.014
2196/1059≒1.004
2289/1087≒0.9946
2299/1090≒1.0185
◆広島県 清川 育男 さんからの解答。
十進BASIC(1000桁モード)で規則性を探索してみました。
nの公差は93,103?
mの公差は28,31?
一般項は?
n m 103 31 196 59 299 90 392 118 495 149 588 177 681 205 784 236 877 264 980 295 1073 323 1166 351 1269 382 1362 410 1465 441 1558 469 1651 497 1754 528 1847 556 1950 587 2043 615 2136 643 2239 674 2332 702 2435 733 2528 761 2631 792 2724 820 2817 848 2920 879 3013 907 3116 938 3209 966 3302 994
◆大阪府の高校生 Alpha Omega さんからの解答。
2n/10m≒1となるようなm,nを求めるとは、両辺に常用対数をとって、
log(2n/10m)≒0となるm,nを求めるということ。
整理して log(2)≒m/n
したがってこの問題はlog(2)に近い有理数を探せ、というものに言い換えられる。
電卓より、
log(2)=0.30102999566398119521373889472449…
m/nとして301/1000を使えば2n/10mはもっと1に近づく。
電卓ではここまでいい近似値が出ているので、たとえば、
m = 3010 2999 5663 9811 9521 3738 8947 2449
n = 1 0000 0000 0000 0000 0000 0000 0000 0000
のように、コンピュータなどで計算さえできればいくらでも近づけられる。
まあ、実用的にはm=3,n=10で十分ですね。
◆広島県 清川 育男 さんからの解答。
Alpha Omega さんからの解答を十進BASICでプログラムしました。
REM 1より大きい場合 LET X=1+LOG2(5) LET Y=7-3*LOG2(5) FOR M=1 TO 3000000000 FOR N=INT(M*X)+1 TO INT(M*X+Y) PRINT N;M NEXT N NEXT M END
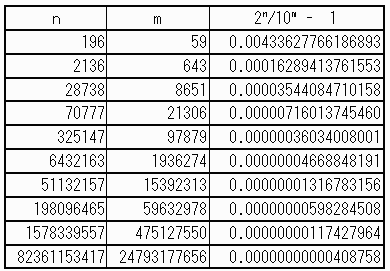
◆愛知県 Y.M.Ojisan さんからの解答。
1より大きいものに限定した代表的解を下表に示す。

【求め方】
23/10=0.8<1 と 210/1000=1.024>1 を用いて
0.8*1.024Pを考える。
この値はp=10(n=103)において1を超過し、
1.024より1に近い1.014..になる。
またその手前のp=9においては
1.024 より1に近い0.990352..になる。
0.990352の方が1.014より1に近いので、
同様に (1.014..)*(0.990352..)Qを考えると
Q=2において1を下回り0.9946…、
Q=1では1.00433..である。
表値はこのようにして逐次計算した値(30桁で計算)である。
【コメント】
| 2n 10m |
≒1 の両辺の常用対数をとると |
log102*n−m=ε,ε≒0
| すなわちlog102= | ε n |
+ | m n |
である。 |
| 従って | m n |
はlog102に近い有理数であり、このとき | ε n |
は0に近い。 |
| しかし | m n |
がlog102に近くても、nが大きいと、εが小さいとは限らない。 |
従って、この問題はlog102を近似する有理数の中でも相対的に分母が小さい物探すことと等価な問題である。