(b>c、b,cは互いに素な自然数)とおくと、
◆静岡県 ヨッシー さんからの解答。
【問題2】
y=aχ(a>1:aは有理数)とおく。
χy=yχ は
χaχ=(aχ)χ と書ける。
変形して、
(χχ)a=χχ・aχ
両辺χχ(>0)で割って
(χχ)(a−1)=aχ
変形して
(χ(a−1))χ=aχ
一般にx>0の範囲で xr(rは実数)は単調増加するので、
χ(a−1)=a
よって
![]()
(b>c、b,cは互いに素な自然数)とおくと、
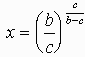
今、特にb=c+1 とおくと、
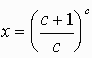
ここで、任意の自然数cにたいし、
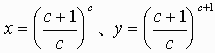
とおくと、題意を満たす有理数 χ,y が無数に作れる。
◆東京都 千葉 英伸 さんからの解答。
【問題1】
ヨッシーさんの問題2の解答の途中までを利用すると、
自然数nと、a>1かつanが自然数になる有理数aで、
na-1=a ・・・(*)
を満たすものがどれだけ存在するか、という問題に帰結します。
(考えやすいようにxの代わりにnを使っています)
aの条件が複雑すぎて、まともに考えるのは大変なので、一般化して、
y=nx-1 ・・・(1)
y=x ・・・(2)
の交点のx座標を求めます。
もちろん、x、yは実数でx>1です。
nが何であっても、(1)、(2)は点(1,1)で交わりますが、
残念ながらx>1に反します。
従って、もう1つの交点(存在するならば)を見つけることになります。
(*)の条件を満たすかどうかは後から考えます。
nについて順番に検討していきます。
n=1のとき、
式(1)は、y=1x-1=1となり、
交点は(1,1)のみ。
よって、n=1のときには解はありません。
n=2のとき、
式(1)は、y=2x-1となり、
交点は(1,1)、(2,2)の2点。
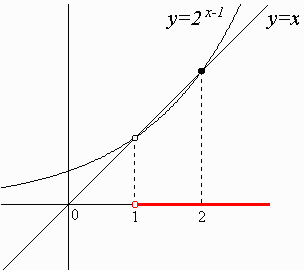
点(2,2)のみ(*)を満たし、a=2です。
n≧3のとき、
(1)、(2)はつねに点(1,1)で交わるので、勘違いしそうですが、
x>1において、(1)、(2)は交わることはありません。
実際、(1)を微分すると、
y'=nx-1logen
n≧3>eなので、x=1のときの微分係数は、
y'=logen>1 となり、(2) の傾きより大きくなります。
つまり、点(1,1)以外の交点は
0<x<1の区間にあることになります。
(下図はn=5の場合)
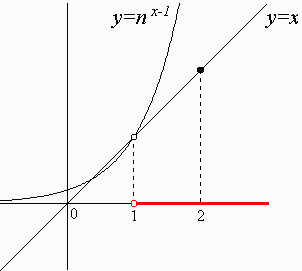
結局、(*)を満たすのは、
n=2、a=2の1組だけです。
元の式については、
x=n=2、y=ax=4なので、
この問題の解は、
(x、y)=(2,4)の1組だけしかありません。