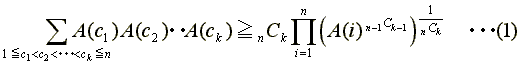
◆沖縄県 jpgr さんからの解答。
【問題1】
| 「 | (1+ | S n |
)n 」が「(1+S)n」の書き間違いとして進めます。 |
| (1+S)n> | (1+ | S n |
)n --(*) |
任意の自然数nについて
(1+A(1))(1+A(2))...(1+A(n)) ≧ (1+S)nで、
等号が成り立つのはn = 1または
n ≧2でA(1) = A(2) =...= A(n)のときである。
1 ≦ k ≦nとなる任意の自然数kについて、
(1+A(1))(1+A(2))...(1+A(n))を展開したとき、
k個のA()の積からなる項はnCk個あり、
そのうち特定のA(i)(ただしiは、1≦ i≦ nとなる自然数)
を含む項は n-1Ck-1個ある。
【例】
n = 4、k = 2、i = 3とすると2個のA()を含む項は、
A(1)A(2)、A(1)A(3)、A(1)A(4)、
A(2)A(3)、A(2)A(4)、A(3)A(4)の6とおり
(6 =4C2)で、
そのうちA(3)を含む項は
A(1)A(3)、A(2)A(3)、A(3)A(4)の3とおり。
(3 = 4-1C2-1)
自然数c1、c2、...、ckが、
1≦c1<c2<...<ck≦nを満たすとする。
これらの項の和について、相加相乗平均の関係を用いて
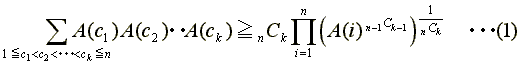
等号はn = 1のときか、
n≧2でA(1) = A(2) =...= A(n)のとき。
ここで、
|
n-1Ck-1 nCk |
= |
(n-1)! (k-1)! (n-k)! |
k! (n-k)! n! | = |
k n |
| nCk | n Π i=1 |
A(i)k/n= | nCk | Sk |
よって
(1+A(1))(1+A(2))...(1+A(n))
| = 1+ | n Σ k=1 | [ | Σ 1≦c1<c2<...<ck≦n |
{A(c1)A(c2)...A(ck)}] |
| ≧1+ | n Σ k=1 | ( | nCk | Sk | ) |
| = (1+S)n |
したがって、(1+A(1))(1+A(2))...(1+A(n)) ≧ (1+S)nが成り立ち、等号が成り立つのは、
n = 1またはn≧2でA(1) = A(2) =...= A(n)のときである。
【問題2】
n = 1のとき 2C1= 21。
n≧2のとき、2nCn>2nである。
数学的帰納法を使って証明する。
n = 1のとき、2n = 21 = 2、
2nCn=2C1= 2なので、
2C1= 21である。
n = 2のとき、2n = 22 = 4、
2nCn=4C2= 6なので、
4C2>22で、
|
4C2 22 |
> 1。 |
2以上の自然数kについて、
|
2kCk 2k |
> 1が成り立つとすると、n = k+1のとき |
|
2(k+1)Ck+1 2k+1 |
| = | 1 2k+1 |
{2(k+1)}! (k+1)! (k+1)! |
| = | 1 2k+1 |
(2k+2) (2k+1) (2k)! (k+1)2 k! k! |
| = 2 { | 2k+1 k+1 |
2kCk 2k |
} |
| > | 2kCk 2k |
| >1。 |
よってn = kのときに成り立てば、n = k+1のときについても同様に成り立つので、2以上の任意の自然数について
2nCn>2nが成り立つ。
問題1は未だに自信がありません。
特定のnについてだとまだやりやすいのですが、一般化されるととたんにやりづらくなるように感じます。
◆大阪府 macsyma2e さんからの解答。
【問題1】
| It is clear that(1+S)n≧ | (1+ | S n |
)n, the eqaulity holds if and only if n=1. |
If n=1, the l.h.s.=1+A(1)= the r.h.s.
If n=2, there exist positive numbers x, y,
such that A(1)=x2, A(2)=y2,
and(1+x2)(1+y2)-(1+xy)2 =(x-y)2 holds,
hence the l.h.s. ≧ the r.h.s.
Now fix n as an arbitrary positive integer.
Then, by using
(1+A(1))...(1+A(n)) ≧(1+[A(1)...A(n)]1/n)n ..... H1
(1+A(n+1))...(1+A(2n))≧(1+[A(n+1)...A(2n)]1/n)n .... H2,
we can obtain
(1+A(1))...(1+A(2n))≧(1+[A(1)...A(2n)]1/(2n))2n,
because
(1+A(1))...(1+A(2n))
=(1+A(1))...(1+A(n))(1+A(n+1))...(1+A(2n))
≧[(1+[A(1)...A(n)]1/n)(1+[A(n+1)...A(2n)]1/n)]n (by H1,H2)
≧[(1+{ [A(1)...A(n)A(n+1)...A(2n)]1/n }1/2)2 ]n (by the case of n=2)
=(1+[A(1)...A(2n)]1/(2n))2n.
Hence the inequalities
(1+A(1))...(1+A(n)) ≧(1+[A(1)...A(n)]1/n)n for n=2k, all k=1,2,3,...
are deduced inductively.
Next fix n as an arbitrary positive inetger, again. By using
(1+A(1))...(1+A(n+1)) ≧(1+[A(1)...A(n+1)]1/(n+1))n+1 ..... H
as A(n+1)=[A(1)...A(n)]1/n,
we can obtain
(1+A(1))...(1+A(n))≧(1+[A(1)...A(n)]1/n)n,
because
the l.h.s. of H
=(1+A(1))...(1+A(n))(1+[A(1)...A(n)]1/n)
the r.h.s. of H
=(1+[A(1)...A(n)([A(1)...A(n)]1/n)]1/(n+1))n+1
=(1+[A(1)...A(n)]1/n)n+1.
Therefore the inequalities
(1+A(1))...(1+A(n)) ≧(1+[A(1)...A(n)]1/n)n for all n=1,2,3,...
are deduced by backward-induction.
【ひとこと】
Cauchy の後向き帰納法でやってみました.
もし、S=A(1)+...+A(n) という設定なら、
(1+A(1))...(1+A(n))
| ≦ ( | (1+A(1)) +...+(1+A(n)) n |
)n |
| = | (1+ | S n |
)n |
として、不等号を逆向きにした不等式が、相加平均と相乗平均との大小関係から直ちに得られますが...
【問題2】
Let r>1, then for any positive integer n,
r*nCn
| = | n Π k=1 |
(r-1)*n+k k |
| ≧ | n Π k=1 |
(r-1)*k+k k |
| = | rn. |
【ひとこと】
r=2 の場合は、
2nCn
| = | n Σ k=0 | nCk・nCn-k |
| ≧ | n Σ k=0 | nCk |
| = 2n |
としてもいいですね.