◆東京都の中学校3年生 Pad さんからの解答。
DH、BFが一致するような位置から見た投影図を書くとBEとDEは一致する。
AC2=2×52⇔AC=5![]()
DBとACの交点をIとする。
| AからIまでの距離は | 5 2 | 。 |
| 5 2 | :5 |
投影図の描き方がポイントの問題ですね。
◆宮城県 甘泉法師 さんからの解答。
| 問題の趣旨を損なわないので長さを | 1 5 | に縮小する。 |
点Eをxyz軸の原点におくと各点の座標は
A(0,0,2)
B(1,0,2)
D(0,1,2)
G(1,1,0)
平面DBEの方程式は原点を通るので
ax+by+cz=0
点D,Bの座標値を代入して
a+2c=0
b+2c=0
よって方程式は
2x+2y-c=0
直線AGの方程式は点Aをとおることから
| x 1 | = | y 1 | = | z-2 -2 |
直線AGと平面DBEの交点をP(e,f,g)とすると
2e+2f-g=0
| e = f = | g-2 -2 |
| これから P( | 1 3 |
, | 1 3 |
, | 4 3 | ) |
| よってAP= | 3 |
,GP= | 2 3 |
AP:GP =1:2
【コメント】
どういう比か興味があって高校数学を使いました。
◆栃木県 coon さんからの解答。
まずBFとDHが重なるように横から見ます。
対角線AGと平面DBEの交点をHとします。
すると△AB(D)Hと△GEHが1:2で相似となります。
したがってAH:HG=1:2となります。
◆大阪府の中学校2年生 Y.M さんからの解答。
ACとBDの交点をPとしておきます。
(Pは四角形ABCDの中心ですからAP=CP)
この図形を4点AEGCを通る平面で切ります。
平面DPEとAGの交点(Q)はEPとAGとの交点になります。
よって相似の関係により、
AQ:QG=AP:EG=1:2
となります。
答:1:2
◆島根県の中学校3年生 支離滅裂 さんからの解答。
まず、平面(AEGC)を見ます。
辺ACの長さは三平方の定理より、5![]() という数字が出ます。
という数字が出ます。
辺ACの中点をIとします。
そうすると、辺AGと辺IEの交点が切り取った面DBEと対角線AGの接触する所になります。
辺AGと辺IEを関数で表す事が出来ます。
その辺AGと辺IEの交点をJとします。
点Eを原点とし考えます。
辺AGは(x,y)=(0,10)と(x,y)=(5![]() ,0)を通る事が分かります。
,0)を通る事が分かります。
これを代入して、10=b,0=5![]() a+bです。
a+bです。
| これを解いて、y= | −2x |
+10が出ます。 |
| これは、原点と(x,y)=( | 5 2 |
,10)を通る事が分かります。 |
| ここでの | 5 2 |
とはAC(5 |
| これを代入して、10= | 5 2 |
aが出ます。 |
| これを解いて、y= | 4x |
になります。 |
この二つの式を解いて、
| (x,y)=( | 5 3 |
, | 20 3 |
)になります。 |
点Jから辺ACに垂線を引きます。
その交点をKとします。
AK,JKの長さはそれぞれ
| AK= | 5 3 |
,JK= | 10 3 |
, |
| AJの長さは三平方の定理より | 5 3 |
となります。 |
JGの長さは
| 5 |
5 3 |
で | 10 3 |
です。 |
| AJ:JG= | 5 3 |
: | 10 3 |
=1:2になります。 |
∴対角線AGと平面DBEの交点は線分AGを1:2に分ける。
◆山梨県 Footmark さんからの解答。
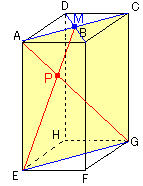
与えられた直方体ABCD-EFGHを4点AEGCを含む平面(注)で切断します。
(薄黄色の面)
すると、明らかに線分AGはこの切断面上にあります。
また、BDの中点MはACの中点でもあり、線分AC上にあります。
ですから、3点BDEを含む平面上にある線分MEもこの切断面上にあります。
それ故、切断面上において線分AGと線分MEは1点Pで交差します。
明らかに、△PMAと△PEGは相似です。
また、MはACの中点ですから、MA:EG=1:2
よって、AP:GP=1:2
【答え】 線分AGを1:2に分ける。
(注)
明らかに4点AEGCは同一平面上にあります。
また、4点AEGCのどの3点も1直線上にありません。
ですから、4点AEGCの任意の3点を含む平面と同じ意味になります。
[ P・S ]
この解法からもお気付きのように、任意の直方体で1:2になります。
ですから、直方体の3辺の長さは必要なかったですね。
◆海外 Londonたぬき さんからの解答。
| → EA |
= |
→ a | (1), |
→ EF |
= |
→ b | (2), |
→ EH |
= |
→ c | (3)とおく。 |
今、線分AGと平面DBEとの交点をIと置くと、Iは平面DBE上の点だから、以下のとおりに表せる。
| → EI |
=m |
→ EB | +n |
→ ED |
= m( | → a |
+ |
→ b | )+n( |
→ a |
+ |
→ c | )=(m+n) |
→ a |
+m |
→ b | +n |
→ c | (4) |
また、Iは線分AG上の点より
| → AI | =k |
→ IG |
(但し k≧0) |
( |
→ EI | - |
→ EA |
)=k( | → EG |
ー | → EI |
) |
それぞれに(1)、(2)、(3)、(4)を代入して整理すると、
(m+n-1) |
→ a | +m |
→ b |
+n | → c |
=-k(m+n) | → a |
+k(1-m) |
→ b | +k(1-n) |
→ c |
題意より |
→ a | , |
→ b |
, | → c |
はそれぞれ互いに平行なベクトルでは無いことから, |
m+n-1=-k(m+n) ・・(5)
m=k(1-m) ・・(6)
n=k(1-n) ・・(7)
| (6),(7)より、m=n= | k 1+k |
(5)にこれを代入して、
| k 1+k |
+ | k 1+k |
-1=-k( | k 1+k |
+ | k 1+k |
) |
| これを解いて k= | 1 2 |
, -1 |
| k≧0より k= | 1 2 |
よって、求める点Iは線分AGを1:2に分割する点。
(感想)
ベクトルを使った解答が見当たらなかったので昔の記憶を頼りに解答をつくってみました。
最近は余りベクトルは流行らないのでしょうか。
3つのベクトルは互いに直交している必要はないので、直方体の他、それをひしゃげた形でも同様
に線分は1:2に分割されることが解ります。