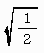
sin(2×π/4)=1
sin(3×π/4)=
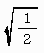
sin(4×π/4)=0
sin(5×π/4)=−
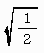
sin(6×π/4)=−1
sin(7×π/4)=−
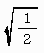
sin(8×π/4)=0
◆東京都 GOFY・和人さんからの解答。
博士:ふむ、おもしろい問題が出されておるのぉ。どうやって解こうかのぅ。
おお、まるでこの問題の為に創られたような数値があるではないか。
sin(1×π/4)=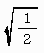
sin(2×π/4)=1
sin(3×π/4)=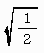
sin(4×π/4)=0
sin(5×π/4)=−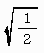
sin(6×π/4)=−1
sin(7×π/4)=−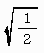
sin(8×π/4)=0
つまり sin2π で1周するのじゃな。
長針Lは短針Sの12倍の早さで回るから、針が重なる時刻を求めるには・・・・
助手:御茶飲み博士!
博士:何だね後夢君? (あとゆめ君です。アトムと読まないで下さい)
助手:時計を3秒間観察したのですが、短針が1周する間に長針が11回追い付き(追い越し)ます。
0時00分00秒0から始めて次に針が重なるのは 12/11時間後、
つまり1時05分27秒272727272727・・・・
博士:もう良い。それで?
助手:角度にすると392.7272727272・・・・
博士:やめなさい。世界が終わるまで続ける気か?
助手:長針と短針がつくる角度の変化は1秒間に0.1090909090・・・
博士:はいはい。おまえは壊れた蓄音機か?いったい何桁まで計算したんじゃ?
助手:*それぞれ428571万桁、56億7千万桁、36524219879桁ですが、どれも割り切れませんでした。
無理数なのでしょうか?
博士:(やれやれ、転馬博士も酔狂なものを創ったものじゃ)
(注:てんうま博士です。ドクター・テンマとは無関係です)
だからどうなのじゃ?
助手:ですから 12/11 をN倍すれば針が重なる時刻になります。
小数点以下を60倍すれば分に、更に小数点以下を60倍すれば秒になります。
博士:なるほど、しかし針が左右対称になる時刻は簡単にゆかんぞ。
ええとsinLπとsinSπの符号が異なって絶対値が等しければ左右対称だから・・・
助手:博士!6時00分00秒を特別な場合として除外すると短針が1周する間に13回針が左右対称になります。
0時00分00秒から始めて次に針が左右対称になるのは12/13時です。
これをN倍すれば・・・・
博士:なるほど。これも算数ときたか。
しかし針が直角になる時刻は算数では解けまい。
sinπとcosπがちょうど90゜の位相になるから・・・・
助手:博士!短針が1周する間に長針は22回直角をつくります。
3時00分00秒から始めて次に直角をつくる時刻は12/22時間後になります。
これをN倍すれば・・・・
博士:なあ、後夢よ、おまえは数学問題を10万馬力の算数で解いてしまうんじゃなぁ。
*428571は1/7の循環部、56億7千万(年)後に弥勒が再来するとされる。
36524219879の365を整数部分にすると1年の日数になる。
助手:ところで博士、さっきこの時計を観察した時に気づいたのですが、この時計は短針が1周する間に30秒遅れます。
博士:ゼンマイとテンプで動く骨董品にしては上出来じゃよ。実生活には支障無いからな。
助手:ええ?? 720日に1回しか正確な時間を示しませんよ?
博士:また10万馬力の算数か・・・
助手:動かない時計なら、短針が2回まわる間に2回、正確な時間を示します。
確率を計算するまでもなく動かない時計の方が正確です!
博士:・・・(天国の転馬博士!この10万馬力の陽電子頭脳は何とかならないものかのぉ)
(ごめんなさい、天国の手塚治虫先生、I・アシモフ先生。笑って許して下さい)
【コメント】
動かない時計なら、1日に2回、正確な時間を示すけれども、
1日に1分ずつおくれる時計は720日に1回しか正確な時間を示さない。
だから動かない時計の方が正確!?
というのは、あの不思議の国のアリスのルイス・キャロルの得意の問題だったそうです。
ところで私は今日、宝塚の手塚治虫記念館に行って来ました。
これも何かのご縁でしょうか。
◆広島県 清川 育男さんからの解答。
まだ昼前で、酔っていなくてすみません。
【問題1】
短針と長針の速さの比は、1:12。
1と12は互いに素である。
重なる回数は、12−1=11(回)。追いかける場合。
(「算数にチャレンジ」で学習しました。)
| 0時から | 12 11 | 時間ごとに重なる。 |
イ)午前9時から午後1時30分までに、
| 108 11 | 時, | 120 11 | 時, | 132 11 | =12時=0時, | 12 11 | 時 |
したがって、4回追い越す。
ロ)午後1時30分から午後6時30分までに、
| 24 11 | 時, | 36 11 | 時, | 48 11 | 時, | 60 11 | 時 |
したがって、4回追い越す。
【問題3、4】
0≦A≦11 対称になる時刻をT分後とする。
| 30×A+30× | T 60 | =360-360× | T 60 |
| T=60× | 12-A 13 |
| ・A=1のときT= | 660 13 |
| 1時 | 660 13 | 分 |
| ・A〜A+1のとき、A時60× | 12-A 13 | 分 |
【コメント】
みごと正解です。
まだ昼なのに、酔っている自分が怖いです。
◆東京都 鳳 奥人 さんからの解答。
【問題1】
hを「時」の数(ただし0≦h<12)、
mを「分」の数(0≦m<60)とし、
yを時計の針が「12」の位置から時計回りに動いた角度とすると、
h時m分における長針の位置は y=6m
同じく短針の位置は y=0.5m+30h
というわけで、この二つの式から、長針と短針が重なるのは
| m= | 60 11 | hを満たす時刻になります。 |
hの各値についてmの値を計算していけばいいですね。
秒以下の単位を省略して書きますと、まず「お昼を食べるまで」は
9:49, 10:54, 0:00, 1:05 の4回。
次の「夕食を食べるまで」は
2:10, 3:16, 4:21, 5:27の4回。
(次は6:32になってしまいます)
【問題2】
Aの時計は1日2回正しい時刻を指す。
Bの時計は・・・一度正しい時刻にあわせたら、次は720日後(厳密には「12時間分の遅れ」)では??
※妻が「そんな時計は捨てちまえーー」と・・・(笑)
【問題3、4】
問題1の式を応用すると、
6m+(0.5m+30h)=360 になればいいわけですね。
| すなわち m= | 720-60h 13 | 。 |
というわけで、a時と(a+1)時の間で左右対称になるのは
| a時 | 720−60a 13 | 分。 |
で、これで計算すると、1時と2時の間は1:50(秒以下省略)に左右対称になります。
ちなみに、他の時刻(同様)はというと
0:55, 2:46, 3:41, 4:36, 5:32,
6:27,
7:23, 8:18, 9:13, 10:09, 11:04。
ところで、この式からは出てこないんですが、0:00というのも数えていいのでしょうか?