『正方形は何個？ Part2』解答

◆神奈川県の小学生　てつろー さんからの解答。

【問題１】

２０個

●　●　○　○

●　●　○　○

○　○　○　○

○　○　○　○
の大きさの正方形が、９個 
●　●　●　○

●　○　●　○

●　●　●　○

○　○　○　○
の大きさの正方形が、４個 
●　●　●　●

●　○　○　●

●　○　○　●

●　●　●　●
の大きさの正方形が、１個 
○　●　○　○

●　○　●　○

○　●　○　○

○　○　○　○
の大きさの正方形が、４個 
○　○　●　○

●　○　○　○
 
○　○　○　●
 
○　●　○　○
の大きさの正方形が、１個 
○　●　○　○

○　○　○　●

●　○　○　○

○　○　●　○
の大きさの正方形が、１個

【問題２−１】

２９個（３０個）

●　●　○　○　○

●　●　○　○　○

○　○　○　○　○

○　○　○　○　○

○　○　○　○　○
の大きさの正方形が、１６個 
●　●　●　○　○

●　○　●　○　○

●　●　●　○　○

○　○　○　○　○

○　○　○　○　○
の大きさの正方形が、９個 
●　●　●　●　○

●　○　○　●　○

●　○　○　●　○

●　●　●　●　○

○　○　○　○　○
の大きさの正方形が、４個 
●　●　●　●　●

●　○　○　○　●

●　○　○　○　●

●　○　○　○　●

●　●　●　●　●
の大きさの正方形を含むとすれば、１個と数えて３０個

【問題２−２】

５０個

Ａ

　●　●　○　○　○

　●　●　○　○　○

　○　○　○　○　○

　○　○　○　○　○

　○　○　○　○　○
の大きさの正方形が、１６個

Ｂ

　●　●　●　○　○

　●　○　●　○　○

　●　●　●　○　○

　○　○　○　○　○

　○　○　○　○　○
の大きさの正方形が、９個

Ｃ

　●　●　●　●　○

　●　○　○　●　○

　●　○　○　●　○

　●　●　●　●　○

　○　○　○　○　○
の大きさの正方形が、４個

Ｄ

　●　●　●　●　●

　●　○　○　○　●

　●　○　○　○　●

　●　○　○　○　●

　●　●　●　●　●
の大きさの正方形が、１個

Ｅ

　○　●　○　○　○

　●　○　●　○　○

　○　●　○　○　○

　○　○　○　○　○

　○　○　○　○　○
の大きさの正方形が、９個

Ｆ

　○　○　●　○　○

　○　●　○　●　○

　●　○　○　○　●

　○　●　○　●　○

　○　○　●　○　○
の大きさの正方形が、１個

Ｇ

　○　●　○　○　○

　○　○　○　●　○

　●　○　○　○　○

　○　○　●　○　○

　○　○　○　○　○
の大きさの正方形が、４個

Ｈ

　○　○　●　○　○

　●　○　○　○　○

　○　○　○　●　○

　○　●　○　○　○

　○　○　○　○　○
の大きさの正方形が、４個

Ｉ

　○　●　○　○　○

　○　○　○　○　●

　○　○　○　○　○

　●　○　○　○　○

　○　○　○　●　○
の大きさの正方形が、１個

Ｊ

　○　○　○　●　○

　●　○　○　○　○

　○　○　○　○　○

　○　○　○　○　●

　○　●　○　○　○
の大きさの正方形が、１個

【問題２−３】

これはどこを１ｃｍとするかによって違ってくると思いますが…。

○┐
　├この間を１ｃｍとすれば、
○┘

↓問題２−２を見てください。

Ａ＝１×１＝１　　　　　　　　　　　１ｃｍ2
Ｂ＝２×２＝４　　　　　　　　　　　４ｃｍ2
Ｃ＝３×３＝９　　　　　　　　　　　９ｃｍ2
Ｄ＝４×４＝１６　　　　　　　　　１６ｃｍ2
Ｅ＝２×２÷２＝２　　　　　　　　　２ｃｍ2
Ｆ＝４×４÷２＝８　　　　　　　　　８ｃｍ2
Ｇ＝１×２÷２×４＋１×１＝５　　　５ｃｍ2
Ｈ＝１×２÷２×４＋１×１＝５　　　５ｃｍ2
Ｉ＝１×３÷２×４＋２×２＝１０　１０ｃｍ2
Ｊ＝１×３÷２×４＋２×２＝１０　１０ｃｍ2

（１＋４＋９＋１６＋２＋８＋５＋５＋１０＋１０）÷１０＝７
平均７ｃｍ2　だと思います。

◆山梨県　Footmark さんからの解答。

【問題３ー１】

正方形の右上の頂点になることができる点の数は

２点で１辺を成す正方形の時　　　　：　(ｎ−１)2
３点で１辺を成す正方形の時　　　　：　(ｎ−２)2
４点で１辺を成す正方形の時　　　　：　(ｎ−３)2
　　　　　　　　↓
(ｎ−２)点で１辺を成す正方形の時　：　３2
(ｎ−１)点で１辺を成す正方形の時　：　２2
ｎ点で１辺を成す正方形の時　　　　：　１2

ですから求める正方形の数は

n-1
Σ
i=1		ｉ2 ＝ ｎ(ｎ−１)(２ｎ−１)
６

［答え］　 ｎ(ｎ−１)(２ｎ−１)
６		　個

【問題３ー２】

上の各正方形において、頂点の位置を４辺上を時計回りにずらすことができるので

２点で１辺を成す正方形が元の時　　　　：　１(ｎ−１)2
３点で１辺を成す正方形が元の時　　　　：　２(ｎ−２)2
４点で１辺を成す正方形が元の時　　　　：　３(ｎ−３)2
　　　　　　　　↓
(ｎ−２)点で１辺を成す正方形が元の時　：　(ｎ−３)３2
(ｎ−１)点で１辺を成す正方形が元の時　：　(ｎ−２)２2
ｎ点で１辺を成す正方形が元の時　　　　：　(ｎ−１)１2

ですから求める正方形の数は

n-1
Σ
i=1		(ｎ−ｉ)ｉ2 ＝ ｎ2(ｎ2−１)
１２

［答え］　 ｎ2(ｎ2−１)
１２		　個

【問題３−３】

ｎ→∞のとき， Ｅ(ｎ)
ｎ2		 は０になってしまいます。

設定が違っているのでは？

点同士の最短距離を１とすると、考えられる正方形の面積は以下のとおりです。
【問題３−２】の解と同順です。

１2(ｎ−１)2
２2(ｎ−２)2 ＋ ２(１2)
３2(ｎ−３)2 ＋ ２(１2＋２2)
　　　　　　↓
ｉ2(ｎ−ｉ)2 ＋ ２{１2＋２2＋…＋(ｉ−１)2}
　　　　　　↓
(ｎ−２)2２2 ＋ ２{１2＋２2＋…………………＋(ｎ−３)2}
(ｎ−１)2１2 ＋ ２{１2＋２2＋…………………＋(ｎ−３)2＋(ｎ−２)2}
ですから、すべての合計は

n-1
Σ
i=1		ｉ2(ｎ−ｉ)2＋２ n-2
Σ
i=1		ｉ2{(ｎ−１)−ｉ}

これを解くとｎの５次式になる筈です。
一方、４点が正方形の頂点になる組合せの数は【問題３−２】の解のようにｎの４次式です。

ですから ｎ→∞のとき， (ｎの５次式)
n2(ｎの４次式)		 は０になります。

◆愛知県　Y.M.Ojisan さんからの解答。

【問題３の一部解答】

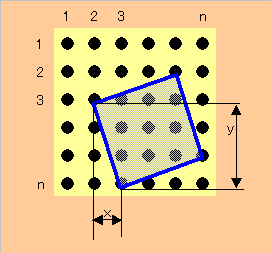
上図のように定義すると、
ｘ＋ｙ≦ｎ−１　ｘ≧０　ｙ≧１　で重複無く正方形が作れる。

この正方形は辺の長さｘ＋ｙの傾かない正方形に内接しており、
後者の数は(n-x-y)2である。

従って、ｘ＋ｙ≦ｎ−１条件下で

総数＝n-1
Σ
x=0		 n-1
Σ
y=1		(n-x-y)2

総面積＝n-1
Σ
x=0		 n-1
Σ
y=1		(x2+y2)(n-x-y)2

である。

ｘ＋ｙ＝Ｉ　ｘ−ｙ＝２Ｋ　に置き換えると、

総数＝n-1
Σ
I=1		 I/2-1
Σ
K=-I/2		(n-I)2＝ ｎ2(ｎ2−１)
１２

総面積＝n-1
Σ
I=1		 I/2-1
Σ
K=-I/2		 I2+(2K)2
２		 (n-I)2＝1
180		 n2(n2-1)(2n2+7)

【問題３−２】

総数　 ｎ2(ｎ2−１)
１２		 　個

【問題３−３】

期待値を言うとき、どのような確率過程か明確でなければなりません。

（Ａ）まず簡単に　ｎ2個の点から任意に４点えらび、それが最初に正方形になった（有効）時の面積の期待値とする。
この場合は【問題３−２】で数えた正方形１個が、有効な４点１組に対応しており、全て同じ確率です。

よって、答えは

総面積
総数		 ＝2
180		 ｎ2／1
12		 ＝２
１５		 ｎ2　　　(@n=∞)

Ｅ(ｎ)
ｎ2		 ＝２
１５		　　　(@n=∞)

（Ｂ）もし、点を４個選んで正方形でないときは面積０とするとすると、
総数＝Ｏ（ｎ8）なので

Ｅ(ｎ)
ｎ2		 ＝０　　　(@n=∞)

（Ｃ）もし、街頭でアンケートを取れば、多分普通の□か４５度傾斜の◇が殆どで、少し傾いた正方形を選ぶ人はあまりいないでしょう。
この場合計算してみると、期待値は

1
12		 (n2+1)n+1
n-1		 　付近なので

Ｅ(ｎ)
ｎ2		 ≒１
１２		　　　(@n=∞)

【Ｐ．Ｓ．】

（Ｃ）は実際は美的感覚からもっと偏るような気がします。
（Ｃ）がどうなるかみんなで参加する実験コーナーにするとおもしろいかもしれませんね。

◆山梨県　Footmark さんからの解答。

【問題３ー３】

最初に置いた式が間違っていました。
点同士の最短距離を１とします。

一番大きな正方形の辺と平行な辺をもつ正方形を「元の正方形」と呼ぶことにすると、 「元の正方形」の各頂点を、最初の位置から４辺上を時計回りに等距離ずらしてもやはり正方形です。

「元の正方形」の１辺の長さがｉの時、「ずらしてできる正方形」のそれぞれ面積は３平方の定理より

　　　１ずらしてできる正方形：１2＋(ｉ−１)2
　　　２ずらしてできる正方形：２2＋(ｉ−２)2
　　　３ずらしてできる正方形：３2＋(ｉ−３)2
　　　　　　　　　　　↓
(ｉ−３)ずらしてできる正方形：(ｉ−３)2＋３2
(ｉ−２)ずらしてできる正方形：(ｉ−２)2＋２2
(ｉ−１)ずらしてできる正方形：(ｉ−１)2＋１2
上の各数字は、＋の左側と右側で合計２回出現しますから、これらの合計面積は

２{１2＋２2＋…＋(ｉ−１)2}

ですから、元の正方形も含めると

　２{１2＋２2＋…＋(ｉ−１)2}＋ｉ2
＝２(１2＋２2＋…＋ｉ2)−ｉ2
＝ ２
６		 ｉ(ｉ＋１)(２ｉ＋１)−ｉ2
＝ ２ｉ3＋ｉ
３

これは元の正方形の１辺がｉの時、その４辺上に頂点をとるすべての正方形の合計面積です。
ですから、考えられるすべての正方形の合計面積Ｓは【問題３−１】の解法と同じ考え方をすると、

Ｓ＝ n-1
Σ
i=1		 (ｎ−ｉ)2(２ｉ3＋ｉ)
３
　＝ ２
３		 n-1
Σ
i=1		 (ｎ−ｉ)2ｉ3＋ １
３		n-1
Σ
i=1		 (ｎ−ｉ)2ｉ

ところで、【問題３−２】の結果より

Ｅ(ｎ)
ｎ2		＝ １２Ｓ
ｎ6−ｎ4

分母はｎの６次式です。

ｎ→∞のときの Ｅ(ｎ)
ｎ2		を求めるので、Ｓはｎの６次以上の項のみで十分です。

１
３		 n-1
Σ
i=1		 (ｎ−ｉ)2ｉ は、ｎの４次式です。

それ故、

Ｓ＝ ２
３		 n-1
Σ
i=1		 (ｎ−ｉ)2ｉ3＋ｐ(ｎ)
　＝ ２
３		 n-1
Σ
i=1		 (ｎ2ｉ3−２ｎｉ4＋ｉ5)＋ｐ(ｎ)
（ただし、ｐ(ｎ)はｎの４次式です。）

上の式でも、ｎが６次になる係数(ｎの０次以上)のみに着目すると、

Ｓ＝ ２
３		( １
４		− ２
５		＋ １
６		 )ｎ6＋ｑ(ｎ)
　＝ １
９０		ｎ6＋ｑ(ｎ)
（ただし、ｑ(ｎ)はｎの５次以下の式です。）

よって、

　 Ｅ(ｎ)
ｎ2
＝ １２Ｓ
ｎ6−ｎ4
＝
１２{ １
９０		ｎ6＋ｑ(ｎ)}
ｎ6−ｎ4
＝
２
１５		ｎ6＋１２ｑ(ｎ)
ｎ6−ｎ4
＝
２
１５		＋１２{ｑ(ｎ)
ｎ6		}
１−１
ｎ2

∴　ｎ→∞のときの Ｅ(ｎ)
ｎ2		は２
１５

　『正方形は何個？ Part2』へ

　数学の部屋へもどる