◆東京都 ぱずきち さんからの解答。
f(n)のpを底とする対数をg(n)とする。
g(0) = 0
g(n+1) = g(n) -1 (g(n) ≧ 1)
g(n+1) = g(n) + b/a (g(n) < 1)
【問題1】
g(0) = 0;
0 ≦ g(n) < 1 ならば
0 < g(n+1) < 1 + b/a
1 ≦ g(n) < 1 + b/a ならば
0 ≦ g(n+1) < b/a
が成立する。
したがって、すべてのnにたいして
0 ≦ g(n) < 1 + b/a < 2
が成立する。
したがって、任意のnに対して
1 ≦ f(n) < p2が成り立つ。
【問題2】
漸化式よりg(n)はb/aのk倍から整数を引いたものであるので、その小数部分はrである。
問題1での考察より
0 ≦ g(n) < 1+b/aであるから
g(n)の整数部は0または1である。
よって、g(n) = r または1+r
f(n) = pr (n = k + [b/a*k])
f(n) = p1+r (n = k + [b/a*k] - 1)
b/a≦ r < 1 の時は、前者しかありません。
[t] はtの整数部分(ガウスの記号)。
【問題3】
問題1、2より
| 0 ≦ g(n) < 1+ |
b ― a | であるから |
| g(n)は |
1 ― a | 間隔で、0から |
a+b-1 a |
一方、漸化式より g(n)が決まればg(n+1)は一意に決まり、
逆にg(n+1)が決まればg(n)が一意に決まる。
したがって、この数列はすべての範囲において周期的であり、1周期の間ですべて異なる値をとる。
そして、1以上でg(n)が最初に0となるnがこの周期数列の最小周期である。
問題2より、g(n)が0となるのはrが0、
則ちb/a*kが整数でn = k + b/a*kの時である。
aとbは素であるので、b/a*kが最初に整数となるのは
k=aの時で、この時n=a+bである。
| よって、g(n)は |
1 ― a | 間隔で、0から |
a+b-1 a |
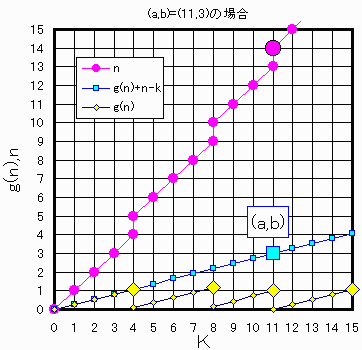
◆愛知県 Y.M.Ojisan さんからの解答。
g(n) = logp(f(n)) とおけば
g(0)=0 ----(1)
g(n+1)=g(n)−1 g(n)≧1 ---(2)
g(n+1)=g(n)+b/a g(n)<1 ----(3)
である。
【問題1】
(2)より g(n+1)≧1−1=0
(3)よりg(n+1)≦1+b/a<2
(1)よりg(0)は範囲内である。
よって 1≦f(n)<p2 である、
【問題2】
下図に示すごとく
通常は f(n)=Pr
| [k* |
b ― a | ]≠[(k-1)* |
b ― a | ] のとき |
【問題3】
a+b個
k=aにおいて r=0となり、g(n)=0で元に戻るため、値は有限個である。
aとbは互いに素であるので、0<k<aに対してr=0になることは無い。
k=aにおいて kb/a=bであり、2値をとる場合はこの間にb個である。
よって、周期はa+bでありかつ線形なので値は全て異なる。
