◆山梨県 Footmark さんからの解答。
【答え】
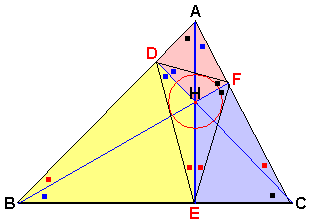
△ABCの頂点A,B,Cより対辺に垂線を引き、垂線の足をそれぞれE,F,Dとすると、
△DEFが周長が最小な三角形です。
【証明】

図のように、3垂線は垂心Hで交わり △ABCを6つの三角形に分割しますが、
明らかに、Hに対して反対側にある3対の三角形同士は、2角が等しいため相似です。
ですから、∠A,∠B,∠Cを2分しているそれぞれの角度は、図に示した関係にあります。
また、対角の和が180°なので、図の赤,黄,青の3つの四角形はどれも円に内接します。
各四角形のそれぞれの外接円において、同じ弧の張る円周角はすべて等しいので、
△DEFの各頂角を2分しているそれぞれの角度は、図に示した関係にあります。
すると、Hは△DEFの各頂角の二等分線の交点で、△DEFの内心です。
そこで、△ABCの各辺を鏡と考えると、△DEFの各辺は明らかに光の道筋です。
これ以外の光の道筋なら、三角形とはならず、
光の道筋に従わない三角形なら、『フェルマーの原理』に反するため最短な道筋ではありません。
よって、図に示した△DEFが、周長が最小な三角形です。
証明は終わりです。
【補足】
『フェルマーの原理』:光は所要時間が最少の道筋を採る。
◆出題者のコメント。
まず初めにお詫びをします。
問題を
鋭角三角形ABCの3辺BC、CA、AB上に、それぞれ点D、E、Fをとる。
このとき、三角形DEFの周が最小になるのは、どんなときでしょうか。
と、すべきでした。
3点D、E、Fが慣れている位置と違い、やりにくかったのではないでしょうか。
この場を借りてお詫びします。
今更訂正もできませんので、この位置のまま話を進めます。
Footmark さんの【答え】については、正解です。
【証明】については、私にはよく分からない部分があって、判断できません。
次の部分について、いくつか質問をしてもよろしいでしょうか?
>すると、Hは△DEFの各頂角の二等分線の交点で、△DEFの内心です。
>そこで、△ABCの各辺を鏡と考えると、△DEFの各辺は明らかに光の道筋です。
>これ以外の光の道筋なら、三角形とはならず、光の道筋に従わない三角形なら、
>『フェルマーの原理』に反するため最短な道筋ではありません。
1.点Hが△DEFの内心であることは、この証明でどのような役割を果たしているのでしょうか?
2.垂線の足である点Eから出発して、→F(垂線の足)→D(垂線の足)→Eと、たどると、 垂線の足である点Eから出発して、他の経路をたどった場合より短くなるのは、 この説明で分かります。
垂線の足でない点Eから出発して、経路が最短となるように、→F(垂線の足でない)→D(垂線の足でない)→Eと、たどった場合より、 短くなることの説明も含まれているのでしょうか?
◆山梨県 Footmark さんからのコメント。
【質問1について】
△DEFの内心Iが、ID⊥AB , IE⊥BC , IF⊥CA であるならば、3辺DE,EF.FDは光の道筋です。
△DEFの内心Iが、ID⊥AB , IE⊥BC , IF⊥CA でないならば、3辺DE,EF.FDは光の道筋ではありません。
【質問2について】
3辺が光の道筋となる三角形は、解答で示した△DEF唯一しか存在しません。
【簡単な証明】