仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
亂栤戣侾亃
摎偊丂侽丅
亂栤戣俀亃
俉夞偱嵎偑侽偵側傞応崌丅侽乣俋傪巊偭偰
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 侾 | 丂丂 | 俋 | 丂丂 | 俆 | 丂丂 | 俋 |
| 丂 | 係 | 丂 | 丂丂 | 丂 | 俉 | 丂 |
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 俋 | 丂丂 | 侾 | 丂丂 | 俋 | 丂丂 | 俆 |
| 丂 | 係 | 丂 | 丂丂 | 丂 | 俉 | 丂 |
| 丂 | 侾 | 丂 | 丂丂 | 丂 | 侾 | 丂 |
| 侽 | 丂丂 | 係 | 丂丂 | 係 | 丂丂 | 侽 |
| 丂 | 俋 | 丂 | 丂丂 | 丂 | 俋 | 丂 |
| 丂 | 係 | 丂 | 丂丂 | 丂 | 係 | 丂 |
| 侾 | 丂丂 | 俋 | 丂丂 | 俋 | 丂丂 | 侾 |
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 丂 | 俆 | 丂 | 丂丂 | 丂 | 俆 | 丂 |
| 侽 | 丂丂 | 俉 | 丂丂 | 俉 | 丂丂 | 侽 |
| 丂 | 俋 | 丂 | 丂丂 | 丂 | 俋 | 丂 |
| 丂 | 俉 | 丂 | 丂丂 | 丂 | 俋 | 丂 |
| 俆 | 丂丂 | 俋 | 丂丂 | 侽 | 丂丂 | 俉 |
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 俆 | 丂 |
| 丂 | 俋 | 丂 | 丂丂 | 丂 | 俋 | 丂 |
| 係 | 丂丂 | 侽 | 丂丂 | 俉 | 丂丂 | 侽 |
| 丂 | 侾 | 丂 | 丂丂 | 丂 | 俆 | 丂 |
忋婰傪係偺忚梋偱暘椶偡傞偲丄
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侾 | 丂 |
| 侾 | 丂丂 | 侾 | 丂丂 | 侽 | 丂丂 | 侽 |
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侾 | 丂 |
俀偮偺僷僞乕儞偵側傝傑偡丅
亂栤戣係亃
侾侽夞偱嵎偑侽偵側傞応崌丅侽乣侾俁傪巊偭偰
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 俀 | 丂丂 | 13 | 丂丂 | 俈 | 丂丂 | 13 |
| 丂 | 俇 | 丂 | 丂丂 | 丂 | 11 | 丂 |
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 13 | 丂丂 | 俀 | 丂丂 | 13 | 丂丂 | 俈 |
| 丂 | 俇 | 丂 | 丂丂 | 丂 | 11 | 丂 |
側偳丅
忋婰傪係偺忚梋偱暘椶偡傞偲丄
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 俀 | 丂丂 | 侾 | 丂丂 | 俀 | 丂丂 | 侾 |
| 丂 | 俀 | 丂 | 丂丂 | 丂 | 俁 | 丂 |
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 侾 | 丂丂 | 俀 | 丂丂 | 侾 | 丂丂 | 俀 |
| 丂 | 俀 | 丂 | 丂丂 | 丂 | 俁 | 丂 |
丂係偺忚梋偵娭學偟偰偄傞偙偲偼悇棟偱偒傑偡偑丄擟堄偺俶夞偵偮偄偰偺堦斒夝偼傑偩敊慠偲偟偰偄傑偡丅
傗偭偲係偵娭學偡傞栤戣偑偱傑偟偨偹丅
亂僐儊儞僩亃
丂俶偺幃偱堦斒夝傪昞尰偡傞偺偼戝曄偦偆側偺偱丄曽朄傪椺偱愢柧偟偰傕傜偊偽廫暘偱偡丅
栤戣俁偺乽侽偵側傞徹柧乿偵偍偄偰傕丄嬼婏惈傪峫偊傞偙偲偼廳梫偱偡丅
嬤擔拞偵乽俵埲壓偺悢乿偱偱偒傞僷僞乕儞傪昞帵偡傞僾儘僌儔儉傪宖嵹偟傑偡丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
亂栤戣係亃
丒侾俀夞
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 俇 | 丂丂 | 37 | 丂丂 | 俉 | 丂丂 | 50 |
| 丂 | 17 | 丂 | 丂丂 | 丂 | 23 | 丂 |
丒侾俁夞
| 丂 | 侽 | 丂 | 丂丂 | 丂 | 侽 | 丂 |
| 俈 | 丂丂 | 44 | 丂丂 | 24 | 丂丂 | 44 |
| 丂 | 20 | 丂 | 丂丂 | 丂 | 37 | 丂 |
婯懃惈偑傛偆傗偔尒偊偰偒傑偟偨丅
亂僐儊儞僩亃
丂抁偄夞悢偱廔傢偭偰偟傑偆応崌偲丄偐側傝偺夞悢懕偔応崌偺僷僞乕儞偑柧傜偐偵堘偄傑偡丅
偦傟傪暘愅偡傟偽丄挿偔懕偔僷僞乕儞傪尒偮偗傞偙偲偑偱偒偦偆偱偡丅
僾儘僌儔儉傕嵹偣傑偟偨丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
| 夞悢 | 0偺捈慜 | 俙 | 俛 | 俠 | 俢 |
| 俉 | 係 | 侽 | 侾 | 係 | 俋 |
| 俋 | 係 | 侽 | 俀 | 俆 | 11 |
| 10 | 係 | 侽 | 俀 | 俇 | 13 |
| 11 | 俉 | 侽 | 俆 | 14 | 31 |
| 12 | 俉 | 侽 | 俇 | 17 | 37 |
| 13 | 俉 | 侽 | 10 | 29 | 64 |
| 14 | 16 | 侽 | 17 | 48 | 105 |
| 15 | 16 | 侽 | 20 | 57 | 125 |
| 16 | 16 | 侽 | 24 | 68 | 149 |
| 17 | 32 | 侽 | 57 | 162 | 355 |
忋婰偺A,B,C,D偼嵟弶偵壜擻偲側傞嵟彫偺悢偱偡丅
僸儞僩偵偁傞夞悢偑戝偒偔側傞応崌偩偲巚偄傑偡丅
仧愇愳導丂惵栘偐傜偺夝摎丅
亂栤戣俁亃
丂偙偺栤戣偺徹柧傪宖嵹偟傑偡丅
嵟弶偺係偮偺悢偺嬼悢丄婏悢偵傛傝丄俇捠傝偵暘椶偟傑偡丅
丂侾偺応崌偼丄侾夞偺憖嶌丅
丂俀偺応崌偼丄係夞偺憖嶌丅
丂俁偺応崌偼丄俀夞偺憖嶌丅
丂係偺応崌偼丄俁夞偺憖嶌丅
丂俆偺応崌偼丄係夞偺憖嶌丅
偟偨偑偭偰乽係偮偲傕嬼悢乿偺応崌偺傒徹柧偡傟偽傛偄丅
係偮偺悢傪俙丆俛丆俠丆俢偲偟傑偡丅
| 崱丄 | 俙 乗乗 俀 | 丆 | 俛 乗乗 俀 | 丆 | 俠 乗乗 俀 | 丆 | 俢 乗乗 俀 |
| 俙 乗乗 俀 | 丆 | 俛 乗乗 俀 | 丆 | 俠 乗乗 俀 | 丆 | 俢 乗乗 俀 |
| 師偵 | 俙 乗乗 係 | 丆 | 俛 乗乗 係 | 丆 | 俠 乗乗 係 | 丆 | 俢 乗乗 係 |
丒丒丒拞棯丒丒丒
尦偺係偮偺悢俙丆俛丆俠丆俢偼俉偺攞悢偵側傝傑偡丅
埲壓丄偙偺媍榑傪孞傝曉偡偲丄
俙丆俛丆俠丆俢偼擟堄偺帺慠悢値偵偮偄偰俀n偺攞悢偵側傝傑偡丅丒丒乮仏乯
乮偲偄偆偐丄偦偺応崌偺傒峫偊傟偽傛偄偺偱偡乯
乽俀偮偺悢偺嵎乿偑乽尦偺俀偮偺悢乿傛傝戝偒偔側傞偙偲偼側偄偺偱丄偳偺僗僥僢僾偵偍偄偰傕丄係偮偺悢偺嵟戝抣偑戝偒偔側傞偙偲偼偁傝傑偣傫丅
乮仏乯傛傝丄偙偺傛偆側悢偼侽偟偐偁傝傑偣傫丅
埲忋偺媍榑偐傜丄係偮偺悢偑偄偔偮偱偁偭偰傕丄嵟屻偼侽偵摓払偡傞偙偲偑傢偐傝傑偡丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
婯懃惈偑尒偮偐傝傑偟偨丅
丂丂丂丂丂丂丂倂丂丂倃丂丂倄丂 倅 丂俀丂丂俇丂丂侽丂丂侽丂丂侾丂丂俁 丂俀丂丂俈丂丂侽丂丂侾丂丂俀丂丂係 傪尦偵師乆偵嶌傞偙偲偑弌棃傑偡丅 丂係丂丂俉丂丂侽丂丂侾丂丂係丂丂俋 丂俇偺倄亖侾傪倃亖侾偵丅倄亖乮係亅俀乯亊俀亖係丅 丂丂丂丂丂丂丂丂丂丂丂丂倅亖俀亊係亄侾亖俋丅 丂係丂丂俋丂丂侽丂丂俀丂丂俆丂侾侾 丂俈偺倄亖俀傪倃亖俀偵丅倄亖俋亅係亖俆丅 丂丂丂丂丂丂丂丂丂丂丂丂倅亖俋亄俀亖侾侾丅 丂係丂侾侽丂丂侽丂丂俀丂丂俇丂侾俁 丂俉偺倄亖係亐俀亖俀亖倃偵丅倄亖侾侾亅俆亖俇丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂倅亖乮侾侾亊俀亄係乯亐俀亖侾俁丅 埲忋偺傛偆偵嶌傞偙偲偑弌棃傑偡丅 丂俉丂侾侾丂丂侽丂丂丂俆丂丂侾係丂丂丂俁侾丂 丂俉丂侾俀丂丂侽丂丂丂俇丂丂侾俈丂丂丂俁俈 丂俉丂侾俁丂丂侽丂丂丂俈丂丂俀侽丂丂丂係係丂偙偙偼娫堘偊偰偄傑偟偨丅係係亙俇係丅 侾俇丂侾係丂丂侽丂丂侾俈丂丂係俉丂丂侾侽俆 侾俇丂侾俆丂丂侽丂丂俀侽丂丂俆俈丂丂侾俀俆 侾俇丂侾俇丂丂侽丂丂俀係丂丂俇俉丂丂侾係俋 俁俀丂侾俈丂丂侽丂丂俆俈丂侾俇俀丂丂俁俆俆 俁俀丂侾俉丂丂侽丂丂俇俉丂侾俋俁丂丂係俀俁 俁俀丂侾俋丂丂侽丂丂俉侾丂俀俁侽丂丂俆侽係 俇係丂俀侽丂丂侽丂侾俋俁丂俆係俉丂侾俀侽侾丂 俇係丂俀侾丂丂侽丂俀俁侽丂俇俆俁丂侾係俁侾 俇係丂俀俀丂丂侽丂俀俈係丂俈俈俉丂侾俈侽俆忋婰偺傕偺偑倅偑嵟彫偲側傞傕偺偩偲巚偄傑偡丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
曗懌
32 丂18丂 0 亅丂丂丂丂Y(18)丂丂 亅
丂丂丂丂丂丂丂丂丂丂丂丂193
32 19 0丂 亅 Y(19) Z(19)
丂 丂丂丂丂丂丂丂丂丂丂230 504
64 20 0 Y(18) 2*Z(19)-2*Y(19) 2*Z(19)+Y(18)
丂丂丂丂丂丂 193 548丂丂丂丂丂丂丂 1201
64 21 Y(19) 2*Y(19)+Y(18) 2*Z(19)+Y(19)+Y(18)丂
丂丂丂丂丂丂丂 230 653 1431
64 22 Z(19)-Y(19) 2*Z(19)-Y(19) 3*Z(19)+Y(18)
274 778 1705丂
慟壔幃偼応崌暘偗偺栤戣傕偁傝丄偆傑偔偄偒傑偣傫丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
| 丂 | 値 | 倂 | 倃 | 倄 | 倅 |
| 侾 | 俀 | 侽 | 侾 | 侽 | 侾 |
| 侾 | 俁 | 侽 | 侽 | 侾 | 侾 |
| 侾 | 係 | 侽 | 侽 | 侽 | 侾 |
| 俀 | 俆 | 侽 | 侾 | 俀 | 俁 |
| 俀 | 俇 | 侽 | 侽 | 侾 | 俁 |
| 俀 | 俈 | 侽 | 侾 | 俀 | 係 |
| 係 | 俉 | 侽 | 侾 | 係 | 俋 |
| 係 | 俋 | 侽 | 俀 | 俆 | 侾侾 |
| 係 | 侾侽 | 侽 | 俀 | 俇 | 侾俁 |
| 俉 | 侾侾 | 侽 | 俆 | 侾係 | 俁侾 |
| 俉 | 侾俀 | 侽 | 俇 | 侾俈 | 俁俈 |
| 俉 | 侾俁 | 侽 | 俈 | 俀侽 | 係係 |
| 侾俇 | 侾係 | 侽 | 侾俈 | 係俉 | 侾侽俆 |
| 侾俇 | 侾俆 | 侽 | 俀侽 | 俆俈 | 侾俀俆 |
| 侾俇 | 侾俇 | 侽 | 俀係 | 俇俉 | 侾係俋 |
| 俁俀 | 侾俈 | 侽 | 俆俈 | 侾俇俀 | 俁俆俆 |
| 俁俀 | 侾俉 | 侽 | 俇俉 | 侾俋俁 | 係俀俁 |
| 俁俀 | 侾俋 | 侽 | 俉侾 | 俀俁侽 | 俆侽係 |
| 俇係 | 俀侽 | 侽 | 侾俋俁 | 俆係俉 | 侾俀侽侾 |
| 俇係 | 俀侾 | 侽 | 俀俁侽 | 俇俆俁 | 侾係俁侾 |
| 俇係 | 俀俀 | 侽 | 俀俈係 | 俈俈俉 | 侾俈侽俆 |
| 侾俀俉 | 俀俁 | 侽 | 俇俆俁 | 侾俉俆係 | 係侽俇俁 |
| 侾俀俉 | 俀係 | 侽 | 俈俈俉 | 俀俀侽俋 | 係俉係侾 |
| 侾俀俉 | 俀俆 | 侽 | 俋俀俈 | 俀俇俁俀 | 俆俈俇俉 |
丂偄傠偄傠側娭學幃傪傒偮偗傑偟偨偑丄夝寛偵偼傎偳墦偄姶偠偱偡丅
堦斣僗僢僉儕偟偰偄傞傕偺偼丄
丂倅乮値亅俁乯亖倄乮値乯亅倃乮値乯丅値亞俆
倅乮値乯丄倄乮値乯傪媮傔傞偙偲偑弌棃傟偽丄倃乮値乯偼娙扨偵媮傔傜傟傑偡偑丅
仧搶嫗搒丂Asami 偝傫偐傜偺夝摎丅
亂栤戣俁亃偺暿徹柧
椬傝崌偆捀揰偺悢偺嵎乮戝偒偄曽亅彫偝偄曽乯傪峫偊偰偄傞偺偩偐傜丄偄偔傜憖嶌傪孞傝曉偟偰傕丄
捀揰偺悢亞侽偱偁傞偙偲偵拲堄偡傞丅
偙偙偱丄偡傋偰偺捀揰偑侽偱側偄偲偒偐傜僗僞乕僩偟偰丄偦偙偐傜壗夞憖嶌偟偰傕丄偳偺捀揰偵傕侽偑尰傟側偄偲壖掕偡傞丅
偡傞偲丄擛壗側傞憖嶌偺抜奒偵偍偄偰傕丄楢懕偡傞俀捀揰偺抣偼(偳偺曈偵娭偟偰傕)堎側傞僴僘偱偁傝丄偟偐傕丄
楢懕偡傞俀捀揰偺嵎亙楢懕偡傞俀捀揰偺俵俙倃
偲側傞偙偲偵拲堄偡傟偽丄
乽係捀揰偺俵俙倃乿偲偄偆検偼丄憖嶌傪偡傞搙偵(惓偺抣傪庢傝側偑傜)嫹媊偵扨挷尭彮偟偰備偔偙偲偑暘偐傞偺偱丄偙傟偼柕弬丅
廬偭偰丄偁傞捀揰偵偼壗夞偐偺憖嶌偺屻偵丄侽偑尰傟傞偙偲偑暘偐傞丅
摿偵丄偦偺屻偡傋偰偺捀揰偑侽偱側偔側偭偨偲偟偰傕丄偝傜偵憖嶌傪壗夞偐孞傝曉偡偲丄嵞傃侽偑尰傟傞偙偲偵拲堄丅
師偵丄夵傔偰
乽壗夞憖嶌偟偰傕丄俀偮埲忋偺捀揰偑侽偵側傞偙偲偼側偄乿偲壖掕偡傞丅乧仛
偦偟偰偁傞抜奒(偙偺忬懺傪俿偲柤晅偗傞)偱丄
斀帪寁夞傝偵侽丆冊丆倷丆倸(傕偪傠傫冊丆倷丆倸亜侽)偲側偭偰偄偨偲偟偰傛偄丅
偝偰丄俿偐傜俀夞偺憖嶌偱
|冊-倸|丆|冊亅|冊-倷||丆||冊-倷|亅|倸-倷||丆|倸亅|倸-倷|
偲側偭偰偄傞偑丄
max{|冊-倸|丆|冊亅|冊-倷||丆||冊-倷|亅|倸-倷||丆|倸亅|倸-倷||}
亙max{冊丆倷丆倸}
偱偁傞偐傜丄俿偐傜壗夞偐偺憖嶌傪宱偨屻丄嵞傃侽丆倫丆倯丆倰偲側偭偨偲偒
max{冊丆倷丆倸}亜max{倫丆倯丆倰}丂偱偁傞丅
偙偺傛偆偵偟偰柍尷偵
max{冊丆倷丆倸}亜max{倫丆倯丆倰}亜乧乧
偲壓崀偟偰備偔偙偲偵側傞偑丄柕弬偱偁傞丅
傛偭偰仛偺壖掕偑岆傝偱偁偭偰丄偁傞抜奒偱偼捀揰偵俀屄埲忋偺乬侽乭偑尰傟傞偙偲偑暘偐傞丅
侽偑俀偮尰傟傞丄偁傞忬懺傪俴偲柤晅偗傞丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
Peter J.Kernan 巵丂傛傝E-mail傪偄偨偩偒傑偟偨丅
(member in phys.CWRU.edu.)
Here is an answer for one thousand steps;
0
232452747934020853026132807148642145655460517565287209547557674662918770312575361490951007004176552319647671151545031627828273740559936870 03857811580536690665802994831566781161
660000008422201365653240760511884563984634306302677480306650170072275219857964620620240992761484943440303946484767780620817002166538617322 33421094983669864309012375477227787970
144638202186621062210298133650350498496322623762037621581753603237625074656613255517935646226333747755504150191217091566993839535484514154 401388311514457320273982346593521067843
Here are the important symmetries.
I will not offer a mathematical proof of why it works but rather let the algorithm serve as its own proof.
Perl偱僐亅僨傿儞僌偝傟偨偲偺偙偲偱偡丅
悽奅偼峀偄側乣偲幚姶偟傑偟偨丅
摨帪偵巹偺偮偨側偄塸岅偱傕悢偺婯懃惈偼尵岅傪墇偊偰棟夝偝傟傞傕偺偩偲姶摦偟傑偟偨丅
仧峀搰導丂枹嵷幚 偝傫偐傜偺夝摎丅
昞偺娭學幃偑傢偐傝傑偟偨丅
n亞8偺偲偒
1.x(n)=z(n-3)-z(n-6)-x(n-3)
2.y(n)=y(n-3)+2*x(n)
3.n+1偑俁偺攞悢偺偲偒
丂丂z(n)=x(n)+z(n-1)
偦偆偱側偄偲偒
丂丂z(n)=x(n)+2*z(n-1)
偙傟偱昞偑姰惉偱偒傑偡丅
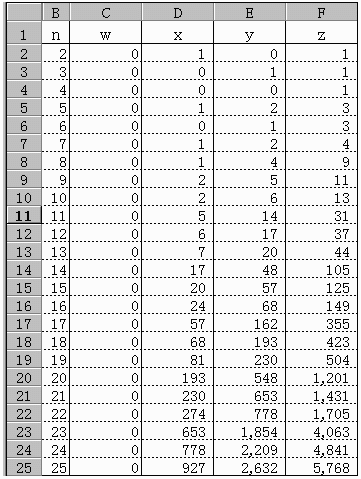
僄僋僙儖偱傗偭偰尒傑偟偨丅

値亖俀偐傜俈傑偱偼僨乕僞傪擖傟偰偔偩偝偄丅
値亖俉偼
x偺棑丂F5-F2-D5
倷偺棑丂E5+2*D8
倸偺棑丂IF(MOD((B8+1),3),D8+F7,D8+F7*2)
偲擖傟屻偼僐僺乕偱OK偱偡丅
嶲峫偵僄僋僙儖偺昞傪揧晅偟傑偡丅
杮摉偼徹柧偑昁梫側傫偱偟傚偆偑丄扤偐偍婅偄両(^_-)