『最小公倍数と素数』 解答

◆愛知県　Y.M.Ojisan さんからの解答。

【問題１】

ｍ≧ｎのとき左辺は０で、与式は成立している。
よって　以下　ｍ＜ｎとする。

[植木算のレンマ]

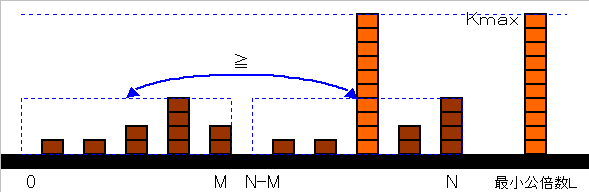
上図のように、０(m)から計測してＰ(m)毎に植木があるとする。

Ｎ−Ｍ(m)地点とＮ(m)地点（Ｎ≧Ｎ−Ｍ≧０）の間にある植木の数を
Ｕ（Ｐ，Ｎ，Ｍ）であらわすとき、下記性質がある。

Ｕ（Ｐ，Ｎ，Ｍ）＝ [ Ｍ
Ｐ		 ]　if Ｎ＝Ｍ

Ｕ（Ｐ，Ｎ，Ｍ）＝ [ Ｍ
Ｐ		 ]　or　[ Ｍ
Ｐ		 ]＋１　else

従って、

Ｕ（Ｐ，Ｎ，Ｍ）−１≦Ｕ（Ｐ，Ｍ，Ｍ）

[レンガ積みのレンマ]

上図のように素数Ｐ（m）の倍数位置に１個、
Ｐ2の倍数位置には２個、
一般にＰKの倍数位置にはＫ個のレンガが詰まれているとします。

Ｂ（Ｎ，Ｍ）を　Ｎ−Ｍ(m)地点とＮ(m)地点（Ｎ≧Ｎ−Ｍ≧０）の間にあるレンガの数とします。
この時、[植木算のレンマ]を用いると、

B(M,M)＝[log(M)/log(P)]
Σ
k=1		 U(PK,M,M)≧ [log(M)/log(P)]
Σ
k=1		{U(PK,N-M,M)-1}

一方、K≧[ log(M)
log(P)		] +1に対して

ＰKの倍数はＮ−Ｍ(m)地点とＮ(m)地点の間には高々１個である。

従って、そのレンガの高さ（Ｋ）の最大値をKmaxとするとき

Ｂ(Ｎ，Ｍ)
＝Σ
K=1〜[log(M)/log(P)]〜Kmax		 U(PK,N-M,M)
＝[log(M)/log(P)]
Σ
K=1		 {U(PK,N-M,M)-1}+Kmax
Σ
K=1		1

以上をまとめると

Ｂ(Ｎ，Ｍ)−Kmax≦Ｂ(Ｍ，Ｍ)

[レンガ塀のレンマ]

最大ｎで、連続ｍ＋１個の整数
ｎ，ｎ−１，ｎ−２，・・・，ｎ−ｍの最小公倍数を
Ｌ(ｎ，ｍ)で表すとする。

この時、Ｌ(ｎ，ｍ)の中の素因数Ｐの冪乗値はKmaxである。

一方　ｎ*(ｎ−１)*(ｎ−２)*・・・*(ｎ−ｍ) 中のＰの冪乗値は
Ｂ（Ｎ，Ｍ）である。

さらに、ｍ！中のＰの冪乗値はＢ（Ｍ，Ｍ）である。

従って、 ｎ*(ｎ−１)*(ｎ−２)*・・・*(ｎ−ｍ)
ｍ！		中のＰの冪乗値は　

Ｂ（Ｎ，Ｍ）−Ｂ（Ｍ，Ｍ）であって、
[レンガ積みのレンマ]より、Kmax　以下である。

各素因数Ｐに対して、以上の関係が成立する。

従って、 ｎ*(ｎ−１)*(ｎ−２)*・・・*(ｎ−ｍ)
ｍ！		≦Ｌ(ｎ，ｍ)である。

[証明]

任意のｎ≧ｍ≧０　に対して　Ｌ（ｎ）≧Ｌ（ｎ、ｍ）は明らかである。
これに[レンガ塀のレンマ]を適用すれば、求める式が得られる。

【問題２】

[レンガ塀のレンマ]の中で示したように
Ｋｍａｘ＝[log(x)
log(P)		 ] ≦log(x)
log(P)
である。

従ってlog(最小公倍数)は

log(L(x))
＝
素数p≦ｘ 		Kmax*log(p)
≦
素数p≦ｘ 		log(x)
＝π(x)log(x)　　―――(1) である。

一方、問題１の定理において m=[x
2		 ] 　の場合を考えると

ｘ≧７が奇数のとき　x=2m+1　とおけば

L(x)
≧ｘ！
(ｍ！)2
＝(２ｍ＋１)！
(ｍ！)2
＝ m
Π
k=1		(4+ 2
k		)
＝ m
Π
k=4		(4+ 2
k		) 7*6*5*4*3*2*1
3*3*2*2*1*1
≧２2m-6×１４０
＞２2m+1
＝２x

ｘ≧8が偶数のとき　x=２ｍ=２ｋ＋２　とおけば

L(x)
≧ ｘ！／(k＋１)／(k！)2
＝２＊(２k＋１)！／(k！)2
＞２＊２2k+1
＝２x

以上より　ｘ≧７において　log(L(x))＞x*log(2)　　―――(2)である。

(1)(2)より　ｘ≧７において　log(2)*x
log(x)		 ＜π（ｘ）である。

ｘ≦６に関しては実際に調べれば、下表に示すように５以上は成立している。

ｘ π（ｘ）
log(2)*x
log(x)
＞　成立判定
２ １ 2 不成立
３ ２ 1.892789261 成立
４ ２ 2 不成立
５ ３ 2.15338279 成立
６ ３ 2.321116843 成立
７ ４ 2.49345031 成立
８ ４ 2.666666667 成立

よって、ｎ≧５　において　log(2)*ｎ
log(ｎ)		 ＜π（ｎ）　である。

【感想】

問題２は　最小公倍数とπの関係(1)になかなか気が付かなくて、悪戦しました。
分かってしまえば問題１より簡単なのですが。

　『最小公倍数と素数』 へ

　数学の部屋へもどる