『数列問題一発勝負』

『数列問題一発勝負』解答

◆東京都　Asami さんからの解答

【問題１】

１より大きければ狭義単調増加。
小さければ狭義単調減少。
よって、１しかない。

【問題２】

p＞1,q≧1のとき(q/p)^q/pは無理数だから、
χ^χ＝２を満たすχは有理数になり得ない。

従ってχは無理数。
このようなχを取ればいいので存在する。
……ってやるのかな？？

【問題３】

1999≡－1

1999¹⁹⁹⁹≡(－1)¹⁹⁹⁹≡－1

以下、この繰り返しなので、余りは４

【問題４】

２ｎ個の数をA₁,A₂,……,A_2nとおく。

これらからｎ個選んだ積χが

であれば、

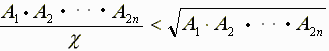
であり、左辺はやはりｎ個からなる積である。

この対応
χ　|→　A₁・A₂・……・A_2n／χ　は

ｎ個の積の値の集合からｎ個の積の値の集合への全単射であるから、
Ｂより大きいＡの個数とＢより小さいＡの個数は等しい。

【問題５】

確かじゃなかったっけ？

◆一平さんからの解答

【問題１】

第ｎ項をａ_nとする。

ａ₁＝ａ、
条件よりａ₁₉₉₉＝ａだから

両辺の対数をとれば、
ａ₁₉₉₈・ｌｏｇａ＝ｌｏｇａ

ｌｏｇａ≠０であればａ₁₉₉₈＝１

従って、またａ₁₉₉₇＝０　となり　ａ＞０であるから矛盾。
従って、ｌｏｇａ＝０だから　ａ＝１・・答

◆東京都　Asami さんからの解答

【問題５】

というのは、どっかでみた(？)いい加減な記憶を頼りにした、全く根拠のない記述です。
どうやら勘はハズれたみたいです。

A₁：＝a
A₂：＝a^a
A₃：＝a^{a^a}

………

とおいて、
このaに対する{A_n}の極限(が存在したとして)をＣとおくと

Ｃ＝a^Ｃ

だからaは

Ｃ＝ｙ^Ｃ

すなわちｙ＝Ｃ^1/Ｃをみたす解ｙになっている。

関数ｆ(χ)＝χ^1/χについて

logｆ(χ)＝(1/χ)logχ

(logｆ(χ))’＝(1/χlogχ)(1－logχ)

というわけで、
χ＝eのときlogｆ(χ)すなわちｆ(χ)は最大値をとる。
(たぶん。ちゃんと確認していないけど。)

極限をもつ最大のaはa＝e^1/eのときで、極限値はe
(実際、このとき{A_n}は上に有界(＜e)な単調増加列なので極限値を持つ)

こんな感じかな？