◆東京都の高校生 小林 哲也 さんからの解答。
分母の値は、
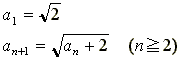
という漸化式を定義して、
| lim n→∞ |
an と書くことができる。 |
なので、
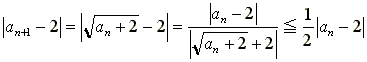
となり、
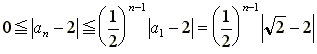
となる。ここで、
| lim n→∞ |
 |
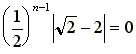となるため、はさみうちの原理より、
| lim n→∞ |
|an-2| = 0 となり |
| lim n→∞ |
an = 2 となる。 |
同様にして、分子の値は 4 となることが証明でき、分数の値は結局 2 となる。
答えだけ求めるのであれば、
分母 = x と置いて、
x2 = 2 + x
となることから、
x = 2 (負はとらない)
と求め、同様にして分子の値を 4 と求めることもできますが、分母、分子それぞれ収束することが証明されていないため、不完全です。
◆愛知県 Y.M.Ojisan さんからの解答。
証明としてはかえって長くなりますが、aNは有界単調増加数列であるので、収束が保証されます。
●有界性
２2−(ａN+1)2=２−ａN なので
０＜ａN≦２ であれば ０＜ａN+1≦２ である。
０＜ａ1＝
≦２ であるから ａNは有界です。
●単調増加性
(ａN+1)2−ａN2
=２+ａN−ａN2
=−(ａN−2)(ａN+1)≧０ for −１≦ａN≦２
ａNは２以下０以上ですから ａNは単調増加数列です。
従って,x2=2+x の妥当な解：２を収束値とすることができます。
◆出題者のコメント。
正解です。
解いていただいてありがとうございました。(^o^)/
◆神奈川県 いわし さんからのコメント。
# 分母だけですが。
小林さんの解にある漸化式
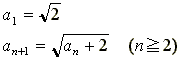
を満たす数列 { an } は、次のように一般項を求めることもできます。
| an = 2 cos | ( | π 2n+1 |
) ・・・(1) |
数学的帰納法により示します。
| a1 = 2 cos | ( | π 4 |
) |
n = k (≧1) のとき (1) を仮定すると、
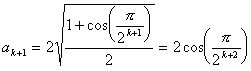
すなわち、n = k+1 のときも (1) は成立しますから、任意の自然数 n に対して (1) の成立が示されました。
よって (1) より、an → 2 (n → ∞) です。
◆東京都の高校１年生 もやし さんからの解答。
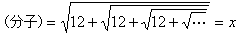とおくと、
これの２乗は１番外側のルートをとるだけだから、
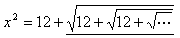となる。
ここで、下線部は（収束とかを考えなくても…が同じ事を繰り返すことを示すので、必然的に）ｘの値と同値だから、
x2＝12＋xを満たす。
したがってこれを解いてx＝−３，４
x＞０から、x＝４
同様に、分母をｙとおけば、これは
ｙ2＝２＋ｙを満たすので、
これを解いてｙ＝−１，２
ｙ＞０から、ｙ＝２
| ゆえに求める値は | ｘ ｙ |
＝ | ４ ２ |
＝２ |