◆宮城県 アンパンマン さんからの解答。
x=npCp=n np-1Cp-1
| x-n p | =n( | np-1Cp-1-1 p | ) |
(np-1)(np-2)...(np-p+1)
≡(-1)p-1 (p-1)!
≡(p-1)!
≡-1 (mod p)
| つまりnp-1Cp-1＝ | k1 p-1 k2 p-1 |
np-1Cp-1は整数であることより
| k1 p-1 k2 p-1 |
は整数のとき | k1 p-1 k2 p-1 |
≡1 (mod p) |
つまりｐ｜np-1Cp-1-1
∴ ｐ｜(x-n)
◆愛知県 Y.M.Ojisan さんからの解答。
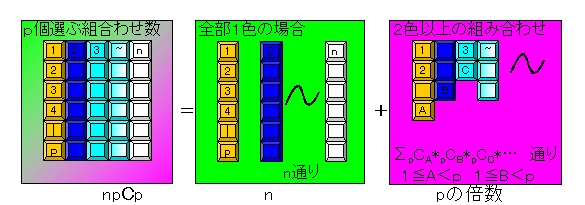
下図に示すようにｐ個ずつｎ組（色）にわける。
ｐ個全て同じ色の場合はｎとおりである。
一方２色以上の場合は、必ずpCZ（１≦Z＜ｐ）を因数に持つ。
| pCZ＝ | ｐ*… Z！… |
である。 |
即ちｐCZはｐの倍数である。
よってｘ−ｎはｐの倍数である。
【蛇足】
組み分けをｎ個ずつｐ色に分けると、各色から１個ずつｐ個の場合と、それ以外の場合に分類できる。
それ以外の場合は各色の対称性から、pCZ（Z：選んだ色数 １≦Z＜p）が係数にかかる。
すなわちそれ以外の組み合わせ数はｐの倍数である。
従って、各色から１個ずつの場合の組み合わせ数：
ｎｐ と ｎ がmod pで等しいかどうかが問題であるが、【解答】より成立する。
ここで両辺をｎで除すと有名なフェルマーの定理が出てくる。
即ち ｎp-1≡1 mod p p:素数
【感想】
こんなに簡単にフェルマーの定理の証明ができるとは驚きです。
◆愛知県 Y.M.Ojisan さんからの解答。
アンパンマンさんの解答は鮮やかです。
定理を使わない省エネタイプにできることをお知らせします。
(n-1)*p=πとして
| x-n n |
| =np-1Cp-1-1 |
| = | (π+(p-1))*(π+(p-2))*....(π+1) (p-1)! |
- 1 |
| = | ｛Kπ+(p-1)!-(p-1)!} (p-1)! |
| = | K'p (p-1)! |
∵ｐは素数であり(p-1)!と公約数を持たない。
また左辺は整数であるから。
◆宮城県 アンパンマン さんからの解答。
(x-n)
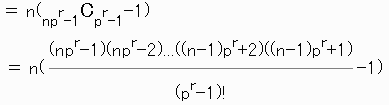
K1,K2は
を満たす最大の整数とすると
| K1＝(npr-1-1)+(npr-2-1)+...+(n-1)+ | [ | n-1 p | ]+[ | n-1 p2 | ]+... |
| K2＝(n-1)pr-1+(n-1)pr-2+...+(n-1)+ | [ | n-1 p | ]+[ | n-1 p2 | ]+... |
K＝ K1-K2
＝ (pr-1-1)+(pr-2-1)+(pr-3-1)+....+(p2-1)+p-1
| ＝ | pr-p p-1 | -(r-1) |
ｎと依存しない。
つまり
はｐで割り切れません。
P(n)
＝｛npr-1,npr-2,...,(n-1)pr+2,(n-1)pr+1}
＝ P0 ∪P1 ∪...∪Pr-1
Pi (n)
＝｛m| m∈P, mはpiで割り切れますがpi+1では割り切れません｝
＝ Qi-Qi+1
ここで
Qi (n)
＝{(n-1)pr＋pi,(n-1)pr＋2pi,...,(n-1)pr＋(pr-i-1)pi}
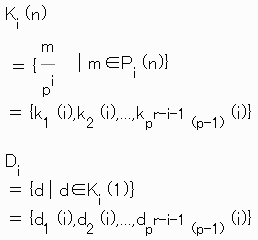
すると
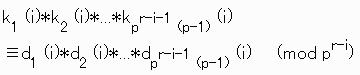
しかし、i＝ r-1のとき、
k1 (i)*k2 (i)*...*kp-1 (i)
＝((n-1)p+1)((n-1)p+2)...((n-1)p+p-1)
| ≡(n-1)p*(p-1)！ | { | 1 1 | + | 1 2 |
+ | 1 3 |
+...+ | 1 p-1 |
}+(p-1)！ (mod p2) |
| 1 1 | + | 1 2 |
+ | 1 3 |
+...+ | 1 p-1 |
| ＝ p | { | 1 1*(p-1) |
+ | 1 2*(p-2) |
+...+ | 1 ((p-1)/2)((p+1)/2) | }より |
k1 (r-1)*k2 (r-1)*...*kp-1 (r-1)
≡(p-1)！
≡d1 (r-1)*d2 (r-1)*...*dp-1 (r-1) (mod p2)
ゆえに
| (npr-1)(npr-2)...((n-1)pr+1) pK | ≡ | (pr-1)！ pK | (mod p2) |
つまり p2 | (x-n)
【コメント】
追加問題は元は「ｐrに変えても成立する（ｒは０以上の整数）」でしたが、
「ｐ2に変えても成立する」に訂正します。
◆茨城県 小川 康幸 さんからの解答。
追加問題の元の方、
つまり、n*pr個の物から、pr個の物を選ぶ方法がx通りある時、
x-n がpで割り切れる事を示します。
実は、もっと強く、x-nはn*pで割り切れることが言えます。
正確に書くと、
が言えます。
【解答】
より、
が示されればよい。
もし、これが示されれば、
となって、
が示される。
これを示す為に、補題を二つほど準備します。
【補題１】
gを任意の0以上の整数、sをs≦pr-2を満たす自然数とするとき、
はpで割り切れる。
【補題２】
gとsを１．と同じものとする。
まず、補題１．を示す。
【補題１の証明】
s+1は、s+1=pt*b、
bはpで割り切れない自然数、tは0以上の整数と書ける。
s+1＜prより、t＜rである。
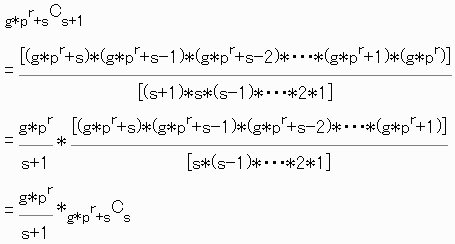
よって、
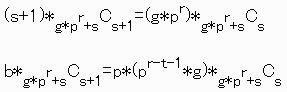
pとbは、互いに素だから、
がpで割り切れる。
終
【補題２の証明】
が成立する。
補題1．より、はpで割り切れるので、
が成り立つので、
終
さて、補題１と補題２で使ったgとsに、
g=n-1，s=pr-2を代入すると、
となる。
よって、補題2．より
が分かる。
が言えた。
解答終
じつは、この問題、『コンビネーション』の中で、私が答えた問題そのものなのですが、その当時の解答（正確に言えば、pによる場合分け）が気に食わないので、新たに解答を作りました。
◆愛知県 Y.M.Ojisan さんからの解答。
【追加問題解答】
先の【解答】において、２色以上の組み合わせでは
pＣZ因子は実際には２個以上必ずあるので、
ｐ２の倍数でもあった。
ｐがｐｒでも、ここまでは同じであり,
（０＜Ｚ＜ｐｒ）がｐの倍数であるかどうかが問題である。
＜補題＞下記は明らかである。
（１）
［ ］をガウス記号とするとき
[x+y] -[x]-[y] ≧0
（２）
<N>をＮの素因数中の素数ｐの数とするとき
| < | x y | >=<x>-<y> x,y自然数 |
（３）
| <N！> = | [logp(N)] k=1 | [ | N pk | ] ただしｐは素数 |
＜証明＞
これらを用いると ０＜Ｚ＜ｐｒなので
[logp(Ｚ)]≦ｒ-1, [logp(ｐr-Z)]≦ｒ-1であるから、
<>
=<ｐr！>-<Z！>-<(ｐr-Z)！>
| = | r k=1 | [ | pr pk | ] | - | r-1 k=1 | [ | Z pk | ] | - | r-1 k=1 | [ | ｐr-Z pk | ] |
| = | r k=r | [ | pr pk | ] | + | r-1 k=1 | {[ | pr pk | ] | - | [ | Z pk | ] | - | [ | pr pk | - | Z pk | ]｝≧１＋０ |
最後は補題（１）を用いた。
すなわち はｐの倍数である。
【Ｐ．Ｓ．】
最初の解答方法にこだわりました。
Ｎの倍数の証明でもこだわれますが、他の方法と比較し、全くメリットがないのでやめておきます。
◆茨城県 小川 康幸 さんからの解答。
追加問題なのですが、どうやら題意をとり違えていたようです。
Y.M.Ojisan さんの解答を参考にして、追加問題を考えました。
●１．
まず、pを素数とすると、
となる事を示します。
その為に、paCpb≡aCb (mod p2)となる事を示します。
paCpb=p*a人の人から、p*b人を選ぶ組み合わせの個数です。
p*a人の人を、p人ずつ、a組に分け（もちろん、重複、漏れはないように選ぶ）、それぞれ、1組、2組、･･･、a組とする。
p*a人の人から、p*b人を選ぶとき、必然的に、
1組からg1人、2組からg2人･･･a組からga人選ぶ事になります。
このとき、g1+g2+･･･+ga=p*bが成立します。
p*a人の人から、p*b人を選ぶ組み合わせの個数 ＝g1、g2、･･･gaがいずれも0またはpとなるような組み合わせの個数 ＋あるgiに対して、0＜gi＜pとなるような組み合わせの個数g1、g2、･･･gaがいずれも0またはpとなるような組み合わせの個数は、
g1、g2、･･･、gaのうち、b個はpで残りは0だから、
aCb個である。
あるgiに対して、0＜gi＜pとなるような組み合わせの個数は、
となる。
g1+g2+･･･+ga=p*b≡0 (mod p)より、
gi以外のあるgjも、pで割り切れない事が分かる。
0≦gj≦pより、0＜gj＜pだから、
は共にpで割り切れる。
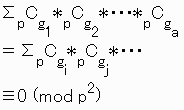
よって、paCpb≡aCb (mod p2)が成立します。
これより、
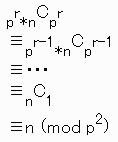となる。
●２．
次に、pが5以上の素数のとき、
となる事を示す。
その為に1．で見たように、
あるgiが0＜gi＜pとなるとき、必ず別のgjが0＜gj＜pとなる。
よって、
p*a人の人から、p*b人を選ぶ組み合わせの個数 ＝g1、g2、･･･gaがいずれも0またはpとなるような組み合わせの個数 ＋ある２つのgi、gjに対してのみ、0＜gi，gj＜pとなるような組み合わせの個数 ＋あるgi、gj、gkに対して、0＜gi，gj，gk＜pとなるような組み合わせの個数、paCpb≡aCb (mod p3)を示す。
あるgi、gj、gkに対して、0＜gi，gj，gk＜pとなるような組み合わせの個数
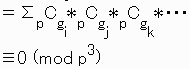
ある２つのgi、gjに対してのみ、0＜gi，gj＜pとなるような組み合わせの個数を求めよう。
gi+gj≡0 (mod p） 0＜gi+gj＜2p より、
gi+gj＝p となるから、
ある２つのgi、gjに対してのみ、0＜gi，gj＜pとなるような組み合わせの個数
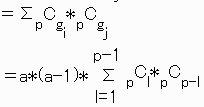
| p-1 l=1 |
pCl*pCp-l |
| ＝ | p l=0 |
pCl*pCp-l-2 |
2*p-1Cp-l≡1 (mod p3)が成り立ちます。
証明は『整数問題一発勝負！！ Part４』を参照ください。
よって、2pCp=2*2*p-1Cp-l≡2 (mod p3)
| p-1 l=1 |
pCl*pCp-l≡(2pCp)-2≡0 (mod p3) |
よって、ある２つのgi、gjに対してのみ、
0＜gi，gj＜pとなるような組み合わせの個数≡0 (mod p3)
が言えます。
paCpb≡aCb (mod p3)が成立する。
よって、
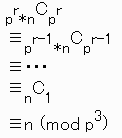となる。