◆広島県 清川 育男 さんからの解答。
【問題1】
ピタゴラス数の必要十分条件
X2+Y2=Z2
X=a2-b2,
Y=2ab,
Z=a2+b2
a,bの一つは偶数、一つは奇数。
n=m2 m≧2 a=m
X2+nY2
=(m2-b2)2+(m2)*(2mb)2
=(m2+b2)
=Z2
X2+nY2=Z2
nが4以上の平方数であればよい。
したがって無数にあることになる。
【問題2】
X2+Y2=Z2
n<0
−n=n1とするとn1>0,
n1=m2
X2=n1Y2+Z2
Z=m2−b2,
Y=2mb,
X=m2+b2
問題1に還元されるのではないでしょうか。
◆静岡県 ヨッシー さんからの解答。
【問題1】
あるひとつの組(X,Y,Z)が見つかれば、それをa(aは自然数)倍した
(aX,aY,aZ)も、条件を満たすので、一組存在することを示せばよい。
1) nが奇数の時
(n=1の時は証明済みなので、n>1とする)
n=2m+1 とおく。(mは自然数)
このとき、X=mY とおくと、
X2+nY2
=m2Y2+(2m+1)Y2
={(m+1)Y}2
より、条件を満たす自然数(X,Y,Z)は存在する。
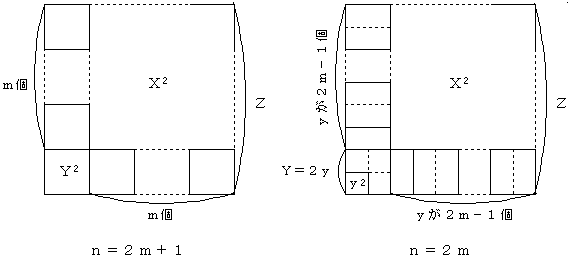
2) nが偶数の時
n=2m とおく(mは自然数)
偶数のY(=2y)に対し、
X=(2m−1)yとおくと、
X2+nY2
=(2m−1)2y2+(2m)(2y)2
=(4m2−4m+1)y2+8my2
={(2m+1)y}2
より、条件を満たす自然数(X,Y,Z)は存在する。
以上より、任意の自然数nについて、
X2+nY2=Z2を満たす
自然数の組(X,Y,Z)は無数に存在する。
【問題2】
nが負の数の時 n=−m(mは自然数)とおくと、
X2+nY2=Z2 は
Z2+mY2=X2 と同値であるので、
問題1と同様に、自然数の組(X,Y,Z)は無数に存在する。
考え方は、図を参照してください。
