『逆さまナンバー』解答

◆広島県　清川　育男さんからの解答。

【問題１】

　χ＝１０００ａ＋１００ｂ＋１０ｃ+ｄ　・・1) 　ｄ＞ａとする。
ｎχ＝ｎ（１０００ａ＋１００ｂ＋１０ｃ＋ｄ）　・・2) とする。

2)−1)
(ｎ−１)χ＝９ｍ_１　・・3) ９の倍数になる。証明は省略。

1)＋2)
(ｎ＋１)χ=１１ｍ_２　 ・・4) １１の倍数になる。証明は省略。

3),4)からｎについて解くと、

ｎ＝

１１ｍ２＋９ｍ１ １１ｍ２−ｍ１

・・5)

これをｍ_２について解くと、

ｍ２＝

９(ｎ＋１) １１(ｎ−１)

ｍ１　・・6)

　ｍ_１＝１１ｍ_３とする。
3),4)に代入すると、
(ｎ−１)χ=９９ｍ_３　・・7)

(ｎ＋１)=９９×

ｎ＋１ ｎ−１

×ｍ３　・・8)

χ＝

９９ ｎ−１

×ｍ３

９９ ｎ−１

×ｍ３=１０００ａ＋１００ｂ＋１０ｃ＋ｄ

９×１１×ｍ_３
＝(ｎ−１)(１０００ａ＋１００ｂ＋１０ｃ＋ｄ)
＝(ｎ−１)χ

１１の倍数は奇数桁の和と偶数桁の和との差が１１の倍数である。証明は省略。

したがって題意（詳細は省略）より、
　ａ＋ｃ＝ｂ＋ｄ　・・9)
ａ＋ｂ＋ｃ＋ｄ＝１８　・・10)

(ｎ＋１)χは５桁（証明は省略）。よって、

ａ＋ｄ＝１０　・・11)

9),10),11)より、
　ｂ＝ａ−１，ｃ＝９−ａ，ｄ＝１０−ａ
　ａ＝１，ｂ＝０，ｃ＝８，ｄ＝９　・・12)
　ａ＝２，ｂ＝１，ｃ＝７，ｄ＝８　・・13)
　ａ＝３，ｂ＝２，ｃ＝６，ｄ＝７　・・14)
　ａ＝４，ｂ＝３，ｃ＝５，ｄ＝６　・・15)

題意を満たすのは、12),13)のときである。

12) １０８９、９８０１、　９８０１＝１０８９×９

13) ２１７８、８７１２、　８７１２＝２１７４×４

　１０８９＋９８０１＝１０８９０
　２１７４＋８７１２＝１０８９０
　０＋８＋１＝９、９＋０＝９と１１の倍数になっている。

　　　　　　　　　答え１０８９、２１７８

ヒントのｎを割り出す解法がわかりません。

【コメント】

　倍数を使ったテクニックには脱帽です。
スマートにｎを出すのは、かなり難しいような気がしています。

◆新潟県　ぽぽぽ　さんからの解答。

最初の４桁の数を 1000a+100b+10c+d とおきます。
（本当はn桁でもよいのですが、とりあえず４桁で考えます）
逆にしたときにN(N＞1)倍になっているとします。

1000a+100b+10c+d = N(1000d+100c+10b+a)

１．最大桁aと最小桁dに注目して満たすべき条件を考えます。

　(1)右辺が４桁の数であることから
　　　N*d≦9

　(2)１の位の関係から
　　　d = N*a mod 10

　(3)トータルの数値の整合性から
　　　N*d≦ a ＜ N(d+1)

２．以上の条件を満たす(a,d)をNを順番に変更することによりしらみつぶしに探していきます。

　　たとえばN=2のときは
　　(1)よりd≦4
　　(2)より(a,d) = (1,2),(2,4),(6,2),(7,4)
　　しかし、(3)を満たすペアはない．．．という感じです。

　　すべて調べると、条件を満たす(a,d)は以下の２組しかありません。
　　○N=4のとき(8,2)、N=9のとき(9,1)

３．上で見つけた２組の数に関して、題意を満たすb（上位２桁目），c(10の位）が存在するか確認します。
　　※できるだけ、４桁という条件を使わずに考えていきます。

　　まずN=4(a,d)=,(8,2)のときを考えます。
　　元々の式に代入して

　　8000+100b+10c+2=8000+400c+40b+32

　　ここでb,cが満たすべき条件を考えます。

　(4)c≦2(右辺が繰り上がりを起こしては最上位桁が8であることに反するため

　(5)c=(4b+3) mod 10 （10の位に注目して）

　(6)c≠0と仮定すれば b≧4　（上位２桁目に注目して）

　○以上の３条件を満たす(b,c)は(7,1)しかないということがわかります。

　N=9,(a,d) = (9,1)も同じように考えると
　(b,c)は(8,0)しかないことがわかります。

４．ここまでの議論は4桁の数ということを使っていませんから、一般的に成り立つはずです。
　　つまり、題意を満たすような４桁以上の数は、

　　87****12,98****01の形に限られるということになります。

５．さて最後に、４桁の数が実際に題意を満たしているか確認します。
　　8712 = 4*2178
　　9801 = 9*1089　となりＯＫです。

　　５桁の場合は100の位をnとおくと
　　87012+100n = 4(21078+100n) より n=9 → 87912

　　98012+100n = 9(21078+100n) より n=9 → 98901 となります。

「感想」

はっきりいって、力わざです。
もっとスマートなやり方があると思いますが、私にはわかりませんでした(^^;;;)。
どなたかお願いします。
プログラムを組んで９桁まで計算させたのですが、間に９が増えていくものと求めた４桁の数が２つ並ぶ場合(８桁以上の場合）となって、なんか不思議な 感じでした。
解答中に考えたいろいろな条件も、答えの見当をつけてから条件を考えるという、非常に姑息な手段を用いてしまいました。

【コメント】

　実はこの問題を出したのは、桁数を増やしたときの答えが不思議だったからなのです。
単純な問題なのですが、答えは何とも意外です。
私も完全に力技で解いてしまいました。

◆広島県　清川　育男さんからの解答。

ｎを割り出す解答

χ＝ａ×1000＋ｂ×100＋ｃ×10＋ｄ，ｄ>ａとする。

　 (ｎ＋1)×χ
＝(ａ＋ｄ)×1000＋(ｂ＋ｃ)×100＋(ｂ＋ｃ)×10＋(ａ＋ｄ)
＝(ａ＋ｄ)×(990＋10)＋(ｂ＋ｃ)×(99＋1)＋(ｂ＋ｃ)×10＋(ａ＋ｄ)
＝(ａ＋ｄ)×990＋(ｂ＋ｃ)×99＋(ｂ＋ｃ)×11＋(ａ＋ｄ)×11)
＝11×((ａ＋ｄ)×90＋(ｂ＋ｃ)×9＋(ｂ＋ｃ)＋(ａ＋ｄ))
＝11×((ａ＋ｄ)×90＋(ｂ＋ｃ)×9＋(ａ＋ｂ＋ｃ＋ｄ))
　　 (ａ＋ｂ＋ｃ＋ｄ＝18は必要条件)
＝11×((ａ＋ｄ)×90＋(ｂ＋ｃ)×9＋2×9)
＝9×11×((ａ＋ｄ)×10＋ｂ＋ｃ＋2)

　したがって、9の倍数でかつ11の倍数である。
　（ａ＋ｄ＝10は必要条件）

　よって(ｎ＋1)×χは５桁の数で、それを10YZ0とする。
1＋0＋Y＋Z＋0＝18　，Y＋Z＝17.............1)
11の倍数は奇数桁の和と偶数桁の和との差が11の倍数。（証明は省略）
1＋Y＋0＝0＋Z　，Z＝Y＋1.................2)
　1)，2)から　Y＝8，Z＝9
したがって、（ｎ＋１）χ＝10890
ａ＋ｄ＝10，1＋4＝5，1＋9＝10
よってｎは4，9である。（１の位の数が0となるのは）
10890/10＝1089 ，1089×9＝9801
10890/5＝2178　，2178×4＝8712

　４桁の時　　　10890＝2×3²×5×11²
　５桁の時　　 109890＝2×3³×5×11×37
　６桁の時　　1099890＝2×3²×5×11²×101
　７桁の時　 10999890＝2×3²×5×11×11111　
　８桁の時　109999890＝2×3³×5×7×11²×13×37

　上記と同様に、ｎ＝4，ｎ＝9で題意を満たす。
一般化されたらどうでしょうか。

（ｎ＋１）χが９の倍数かつ１１の倍数であることが証明され自分では前回の解法よりスマートになったと思っているのですが。
一般化（Ｎ桁）しても、１＋４＝５。１＋９＝１０。
ｎ＝４、ｎ＝９の場合しかないのではと思っています。
すなわち、

（ｎ＋１）χ １０

×９＋

（ｎ＋１）χ １０

＝（ｎ＋１）χ

（ｎ＋１）χ ５

×４＋

（ｎ＋１）χ ５

＝（ｎ＋１）χ

となりますから。

【コメント】

　ようやく力技でない解答ができたような気がします。
だんだん頭の中がすっきりしてきました。
どうもありがとうございました。

◆山梨県　Footmark　さんからの解答。

この問題は、とても面白い問題だと思います。

既にお二人の方によって示されているので証明はしませんが、
９がｍ(≧０)個並ぶのを、＊ｍ＊ で表すものとすると、
１つの解の構成要素は、

１０＊ｍ＊８９ か ２１＊ｍ＊７８

の２つの内のいずれかで、この２つ以外にはありません。

解の個数はこの２つのそれぞれにおいて、桁数の４以上の約数の個数になります。

１２桁を例にすると、４以上の約数は ４、６、１２ 、その個数は３つです。
ですから、両方で６つになります。

具体的に示します。

　１０８９１０８９１０８９　　２１７８２１７８２１７８
　１０９９８９１０９９８９　　２１９９７８２１９９７８　
　１０９９９９９９９９８９　　２１９９９９９９９９７８

約数個の数字の並び(構成要素)が、(桁数／約数)回繰り返します。
その約数個の数字の並び(構成要素)の真ん中には、
(約数ー４)個の９が並んでいます。

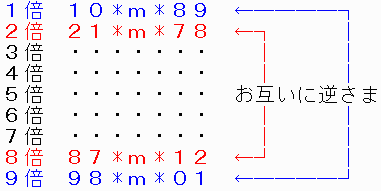
ここで整数倍は、４倍と９倍だけであることを示します。

４倍すれば数字が逆さまになる「２１＊ｍ＊７８」は、
９倍すれば数字が逆さまになる「１０＊ｍ＊８９」の２倍です。

ですから、「１０＊ｍ＊８９」を元の数とすると、
「２１＊ｍ＊７８」は元の数の２倍です。

その逆さまの「８７＊ｍ＊１２」は元の数の８倍(２ X ４)です。
元の数の逆さまの「９８＊ｍ＊０１」は元の数の９倍です。

そこで、元の数の３倍〜７倍も求めてみます。

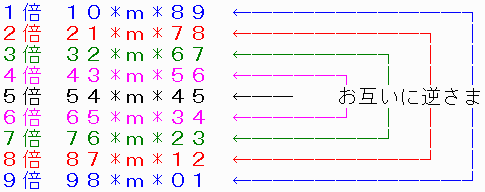
(１倍と９倍),(２倍と８倍)と同様に、
(３倍と７倍),(４倍と６倍)も、お互いに逆さまになります。
（他と同様のため証明省略）
５倍も自分自身を逆さまにさせると、やはり自分自身です。

１０８９ X (１０ーａ) は １０８９ X ａ の逆さまになります。
（ａは １≦ａ≦９ の整数)

ですから、自分の数字の逆さまである相方の数字にするには、

９ １

，

８ ２

，

７ ３

，

６ ４

，

５ ５

，

４ ６

，

３ ７

，

２ ８

，

１ ９

の、いずれかを自分の数字に掛けねばなりません。

この内で整数は

９ １

＝９，

８ ２

＝４，

５ ５

＝１ です。

１倍は意味がないので、整数倍で逆さまにできるのは４倍と９倍だけです。

この問題で、数字の持つ不思議さに本当に驚かされました。

◆東京都　You.O さん　からの解答。

上２ケタが"１０"、下２ケタが"８９"で
これらの間のｍケタがすべて"９"であるような数字の並びを《Ａ_ｍ》、

上２ケタが"２１"、下２ケタが"７８"で
これらの間のｎケタがすべて"９"であるような数字の並びを《Ｂ_ｎ》、

"０"がｋケタ連続した数字の並びを《Ｏ_ｋ》とします。

例えば、

《Ａ_１》：１０９８９，《Ａ_３》：１０９９９８９
《Ｂ_０》：　２１７８，《Ｂ_２》：　２１９９７８
《Ｏ_４》：　００００，《Ｏ_７》：０００００００

のようになります。

これらを整数の構成単位の１種と考えます。
このとき、次のように各ケタの数字が並んで構成される数を９倍または４倍すると数字の並びが逆になります。

☆　９倍すると数字の並びが逆になる数
　―――いくつかの構成単位《Ａ_ｍ》と《Ｏ_ｋ》からなり、それらの構成単位の順序を逆にしてももとの順序と変わらないもの

例．

《Ａ７》《Ｏ12》《Ａ７》　　　　　　　（1099999998900000000000010999999989）
《Ａ４》《Ｏ５》《Ａ１》《Ｏ５》《Ａ４》　　（1099998900000109890000010999989）
《Ａ１》《Ｏ３》《Ａ１》《Ａ１》《Ｏ３》《Ａ１》　（10989000109891098900010989）

例．

《Ｂ６》《Ｂ４》《Ｂ４》《Ｂ６》　　　　（219999997821999978219999782199999978）
《Ｂ３》《Ｏ５》《Ｂ３》《Ｏ５》《Ｂ３》　　　（2199978000002199978000002199978）
《Ｂ１》《Ｏ１》《Ｂ０》《Ｂ０》《Ｂ０》《Ｏ１》《Ｂ１》　（219780217821782178021978）

《Ａ_ｍ》，《Ｂ_ｎ》と逆順の数字の並びをそれぞれ
《Ｃ_ｍ》，《Ｄ_ｎ》とすると、便宜的に次の式が成り立ちます。

《Ａｍ》×９＝《Ｃｍ》，《Ｏｋ》×９＝《Ｏｋ》
《Ｂｎ》×４＝《Ｄｎ》，《Ｏｋ》×４＝《Ｏｋ》

「すべての《Ａ_ｍ》を《Ｃ_ｍ》に変える」

他方、いくつかの構成単位《Ｂ_ｎ》と《Ｏ_ｋ》からなる数を４倍した数は次のようにして得られます。

「すべての《Ｂ_ｎ》を《Ｄ_ｎ》に変える」

また、《Ｏ_ｋ》と逆順の数字の並びは《Ｏ_ｋ》と一致するため、
いくつかの構成単位《Ａ_ｍ》，《Ｂ_ｎ》および《Ｏ_ｋ》からなる数の各ケタの数字の順序を逆にした数は次のようにして得られます。

1. 構成単位の順序を逆にする

2. すべての《Ａ_ｍ》，《Ｂ_ｎ》をそれぞれ《Ｃ_ｍ》，《Ｄ_ｎ》に変える

例えば《Ａ_４》《Ｏ_５》《Ａ_１》《Ｏ_５》《Ａ_４》を９倍すると
《Ｃ_４》《Ｏ_５》《Ｃ_１》《Ｏ_５》《Ｃ_４》となり、

同じく《Ａ_４》《Ｏ_５》《Ａ_１》《Ｏ_５》《Ａ_４》の各ケタの数字の順序を逆にしてもやはり、
《Ｃ_４》《Ｏ_５》《Ｃ_１》《Ｏ_５》《Ｃ_４》となるのです。

　『逆さまナンバー』へ

　数学の部屋へもどる