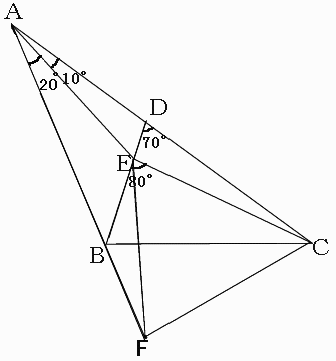
◆海外の大学生 Hirasawa Yasutakaさんからの解答。
(University of North Carolina at Chapel Hill)
Angle DCB = 40:
Triangle AEC is isosceles (angle DCE = 10). Thus AE = CE.
Extend line AB from point B.
Set point F on the extension so that FE = AE = CE...(0)
Tringle EFC is equilateral.
Thus angles ECF = CEF = EFC = 60.
Thus angle BEF = 20...(1)
Triangle EAF is isosceles.
Thus angle EFB is 20...(2)
(1) and (2) imply triangle BFE is isosceles and BE = BF...(4)
(0) and (4) imply triangles EBC and FBC are congruent, thus angles ECB = FCB = 30.
Angle DCB = angle ECB + angle DCE = 30 + 10 = 40.
This problem was so easy.
Took me just 5 minutes to figure out.
Or am I improving?
<青木訳>信用しないでくださいね。(^_^;
答え ∠DCBは40度
△AECは二等辺三角形(∠DCE=10度)。
したがってAE=CE。
点Bから直線ABを延長し、FE=AE=CEとなる点Fを取る。・・(0)
△EFCは正三角形。
したがって
∠ECF=∠CEF=∠EFC=60度
したがって∠BEF=20度。・・(1)
△EAFは二等辺三角形。
したがって∠EFBは20度。・・(2)
(1),(2)より△BFEは二等辺三角形でBE=BF。・・(4)
(0),(4)より△EBCと△FBCは合同。
したがって∠ECB=∠FCB=30度。
∠DCB=∠ECB+∠DCE=30+10=40度。
この問題は簡単でした。
解決するのにたった5分間でした。
それとも私が進歩したのか?・・・

【コメント】
40゜で正解です。
点Fの取り方がポイントなんでしょうね。
角度の計算問題もたくさん作れるものだと感心しています。
◆大阪府の中学校2年生 小悪魔 さんからの解答。
CBを伸ばし、Aから下ろした垂線との交点をGとする。
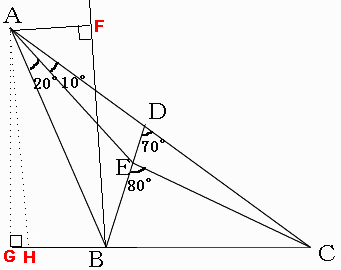
条件から∠ABD=40°
(∠EDC=70°より∠EDA=110°
△AEDの外角なので∠AEB=120°
△ABEの内角から∠ABD=40°)
∠AFB=90°となる点Fを∠ABDの二等分線上にとる。
△AFBは直角三角形だから∠FAD=40°
∠BAH=20°となるように点Aから直線CBに線を引く。
すると、∠FAH=90°となる。
また、∠HAB=∠ABF=20°より
∠FBH=90°であることがわかる。
すなわち、∠ABG=70°。
よって、∠EBC=70°であることがわかる。
△EBCの内角だから∠ECB=30°
よって、∠DCB=40°
◆静岡県 村松 芳子 さんからの解答。
図のようにBDをDの側に延長しAE=EFなるFをとると
∠AEF=60°なので△AEFは正三角形となる。
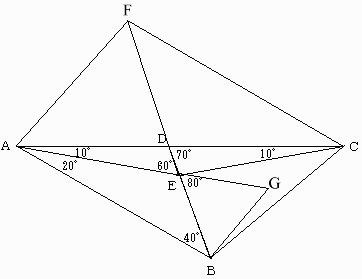
またAEをEの側に延長しBE=EGなるGをとると
∠BEG=60°なので△EBGも正三角形となる。
∠AEB=∠FEG=180°−60°=120°だから,
2辺夾角が等しいので
△AEB≡△FEG
∴∠EFG=20°,∠EGF=40°
一方∠DCE=80°−70°=10°=∠EAD
∴△AECは二等辺三角形
よってAE=EC=EF
∴△FECは二等辺三角形となる。
∴∠EFC=∠ECF=80°/2=40°
また∠FGE=60°−20°=40°だから
円周角が等しく,E,F,C,Gは同一円周上の点である。
∴∠ECG=∠EFG=20°(円周角)
また∠CEG=80°−60°=20°だから
△CEGは二等辺三角形となる。
△EBGは正三角形だからEG=GC=GB
∴△GBCは
頂角80°+60°+20°=160°の二等辺三角形となる。
∴∠GCB=(180°−160°)/2=10°
したがって∠BCD=10°+20°+10°=40°
ところで この問題の大阪の小悪魔さんの解答に疑問があります。
解答文の終わりから5行目の結論がわかりません。
【コメント】
確かに変ですね。
どう直すのがベストでしょうか。