◆愛知県 Y.M.Ojisan さんからの解答。
【答え】 3回
【記号定義】
袋の番号を1〜Nとし、P番目が偽とする。
本物の重さx、偽物の重さx+yとする。
y≠0
表記:[P=Mの場合|P<Mの場合|P>M i.e.M以下に偽物なしの場合]ここで Nが奇数のとき M=N
【方法】
(計測1)
M番の袋の1個の重さを計測
W1=[x+y| x | x ]
(計測2)
1〜M−1番の袋から1個ずつ取り出し計測値平均
W2=[x | x+y/(M-1) | x ]
(計測3)
1〜M−1番の袋から袋の番号個数ずつ取り出し計測値平均
W3=[x | x+2Py/M(M-1) | x ]
M>P(≧1) のとき Mは奇数なので 2P≠M。
即ち W2≠W3 である。
(判定1)
W2=W3≠W1ならば P=M である。
なお、x=W2 x+y=W1
(判定2)
W2≠W3ならば
| P= | M 2 | * | W3-W1 W2-W1 | である。 |
なお、x=W1 x+y=W1+(M-1)(W2-W1)
(判定3)
W2=W1(=W3) ならば P=Nである。
なお、x=W1 x+y=?
全部一致するのはM以下に偽物なしであり、Nが偶数の場合にだけ適用。
【出題者のコメント】
正解です。
私の考えていた方法とほとんど同じです。
つけ加えるとすれば、(問題では要求していませんが、)Nが偶数の場合でもニセ物の重さを求めることが可能な事です。
もし、気が向いたらその方法も考えてみて下さい。
◆愛知県 Y.M.Ojisan さんからの解答。
EXCELをお持ちの方はEXCELのデータでご覧ください。
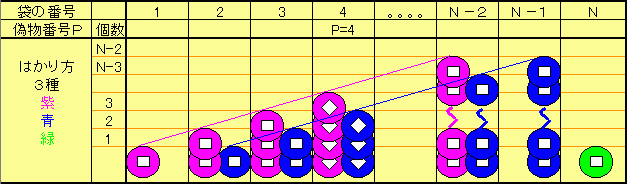
3回 下図のように計測する。

x:本物重さ y+x:偽物重さ
| W= | (N-1)(N-2) 2 | とおく。 |
P:偽物袋番号とするとき表の関係になる。
次に、紫計測値ー青計測値
紫計測値−W×緑計測値を計算する。
このとき、y,Py,(N-2)y,-WyはN>2なので全て0ではない。
従って、まず、Pの範囲を下表の3種に分類できる。

P=Nである。
従って偽物の重さは x+y=緑計測値
本物の重さは x=紫計測値/W
P=N−1である。
従って偽物の重さは
| x+y= | 青計測値−紫計測値 N−2 | +緑計測値 |
本物の重さは x=緑計測値
P=1〜N−2である。
従って偽物の重さは
x+y=(紫計測値−青計測値)+緑計測値
本物の重さは x=緑計測値
これよりPは計算で求まり
| P= | 紫計測値−W×緑計測値 紫計測値−青計測値 |
【感想】
とても良い問題だと思います。
今後数学パズル系の本に取り上げられるのでは。?
残念なのはコインの数がNでなく、N-2個で良いことです。
でも制限無しにすると別の方法が出てきますね。
因みに別方法の1つは
「A=各一個、B=各袋番号個、C=各袋番号2乗個ずつ」と言う方法です。
結論だけ書くと
3(N2-1)Q2+{6(N+1)-6C-(2N+1)(N+1)A}Q+{AC-B2}=0
なるQの2次方程式の小さいほうの解Qをもとめ
x=6Q/N
y=A-Nx
P=(B-Nx(N+1)/2)/y
で求まります。