◆東京都 千葉 英伸 さんからの解答。
まず、問題の整数はpq以上はないことを示したいので、いくつかの命題を順番に示していきます。
(命題1)
整数m、nが|m|<q、|n|<pのとき、
mp=nq → m=n=0
これはp、qは互いに素なので明らかです。
(最小公倍数がpqとうことです)
(命題2)
0≦m1 、m2<qのときに、
m1p、m2pをqで割った余りを r1、r2 とすると、
m1 ≠m2 → r1≠ r2
実際、m1p、m2pをqで割った商をa、bとすれば、
m1p=aq+r1
m2p=bq+r2
と表せるので、 r1=r2 だとすると、
(m1−m2 )p=(a−b)qとなり、
命題1より m1=m2
(命題3)
pq以上の数は、0以上のある整数m、nで
mp+nqと表現できる。
命題2より、q個の整数
0、p、2p、3p、・・・(q−1)pをqで割った余りはすべて異なるので、
これらq個の余りの中に、0からq−1までの整数はすべて1回ずつ現れます。
今、pq以上の整数Aをqで割った余りをrとすると、
A=aq+r
また、このrに対して、0≦m<qを満たすあるmが存在して、
mp=bq+r
ここで、mp<pq≦Aなので、a≧b
よって、
A=mp+(a−b)q=mp+nq
(m、nは0以上の整数)と書くことができます。
さて、問題のmp+nqと書くことのできない整数ですが、
これはpq以上はないことがわかりました。
そこで、0以上pq未満の整数でmp+nqと書くことができる整数を数えます。
0≦m<q、0≦n<pであるものだけ考えれば十分です。
このとき、m1p+n1 q=m2p+n2 qならば、
(m1−m2)p=(n2−n1 )q
なので命題1よりm1=m2 、n1=n2 。
つまり、異なるm、nの組には異なる整数が対応することがわかります。
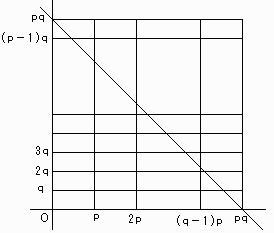
そこで、座標平面上で点(mp、nq)を考えると、数えようとしている整数は
これらの点のうちmp+nq<pqとなる点、
つまり、直線x+y=pqより下にある点に対応します。

図から明らかなように、x方向にq+1個、y方向にp+1個。
このうち、直線x+y=pq上に2点(pq、0)、(0、pq)があるのを考慮すれば点の個数は、
| 1 ―― 2 | (p+1)(q+1)−1 |
これは、0以上pq未満の整数でmp+nqと書くことができる整数の個数なので、問題の答えは、
| pq−( | 1 ―― 2 | (p+1)(q+1)−1) |
| = | 1 ―― 2 | (p−1)(q−1) |
◆広島県 清川 育男 さんからのコメント。
この問題はp,qが素数でなくとも互いに素ということで拡張出来ますね。
(p,q)=1
| 表わせない整数の個数 | (p-1)(q-1) ―――――― 2 |
A=mp+nq≧(p-1)(q-1) はすべて表わせる。
例えば、
p=8,q=21 (8,21)=1
(8-1)(21-1)/2=70 表わせない個数。
A=8m+21n≧140 はすべて表わせる。