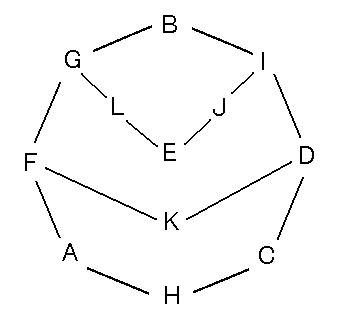
◆静岡県 ヨッシーさんからの解答。
ナイトの動きを図にすると、以下のようになります。

※最初JKLは無いものとして考えると、Eを除く8つのマスが一筆書きになります。
(図の外周の8角形)。
そこに、JKLとEを加えて、図を描きました。
【問題1】
BからKに行く方法は、
B→G→L→E→J→I→D→C→H→A→F→K
B→I→J→E→L→G→F→A→H→C→D→K
【問題2】
BからAに行く方法は、
B→I→J→E→L→G→F→K→D→C→H→A
【コメント】
こうやって図に書いてみると、とても見通しがよいですね。
試行錯誤でもできたでしょうが、このあたりが数学のだいご味でしょうか。
◆群馬県の中学校3年生 松本孝弘さんと布袋寅奏さんからの解答。
(1)B G L E J I D C H A F K
(2)B I J E L G F K D C H A
感想
もともと、チェスがすきだったのでたのしくできた
【コメント】
みごと正解です。
チェスをやっている人は珍しいです。
論理的な考え方が得意なんでしょうね。
◆長崎県 Dr. Berserker さんからの解答。
このような問題の基本的な解き方として、ナイトを文字通りぐるぐるまわすというのが一番やりやすいのではないかと思われます。
というわけで
3,1,6,3,8,5,2,7,5,2,7
チェスの問題では、他に「クイーンプロブレム」というのがありまして、確か、クイーンは、縦横斜め自由に動けたはずですが、これの8個(6個だったかも)の利き筋で、チェス盤(64マス)すべてを埋めてみましょう、というのがありました。
◆石川県の中学校3年生 はげはげ さんからの解答。
3,1,6,3,8,5,8,3,6,1,3
上のが手順です。
◆佐賀県の中学校3年生 池脇 ちづる さんからの解答。
この答えは、コントロールパネルの数字であらわすと
問題1は、
2-4-7-2-5-8-5-2-7-4-2 となります。
問題2は、
3-1-6-3-8-5-2-7-5-2-7 となります。
疑問というか感想は、両方とも11手で解けたけど、これはどんな場合でもそうなのか?と、思いました。
◆岐阜県の中学校3年生 そらとぶざぶとん さんからの解答。
問題1は、
「B,I,J,E,L,G,F,A,H,C,D,K」です。
問題2は、
「B,I,J,E,L,G,F,K,D,C,H,A」です。
◆神奈川県の小学生 てつろー さんからの解答。
【問題1】
2→4→7→2→5→8→5→2→7→4→2 完成
【問題2】
3→1→6→3→8→5→2→7→5→2→7 完成
◆和歌山県の中学校3年生 days01 さんからの解答。
3-1-6-3-8-5-8-3-6-1-3
◆熊本県の中学校1年生 ラッキーボーイ さんからの解答。
<1>I→J→E→L→G→F→A→H→C→D→K
<2>I→J→E→L→G→F→K→D→C→H→A