『近似正三角形』解答

◆富山県　N.C　さんからの解答

ｎ＝３のときに限り、近似的に解いてみます。
正確な値よりもかなり小さい値が得られるものと考えています。
議論のタタキ台にして下さい。

（Ｓｔｅｐ１）近似正三角形であるための条件について

まず、近似正三角形ＡＢＣがあれば、

０．９５＜ ＣＡ
――――
ＢＣ		 ＜ １
―――――
０．９５		 　…(1)

ここで、ε＝１−０．９５とおくと、

　０．９５＝１−ε、

１
―――――
０．９５		 ＝１＋ε＋ε2＋…≒１＋ε

なので、先の式を
１−ε＜ ＣＡ
――――
ＢＣ		 ＜ １＋ε　…(2)

と近似できます。

近似正三角形ＡＢＣの外接円の半径をＲとすると、正弦定理（高校・数I）より

　ＢＣ＝２Ｒ sin(∠Ａ)、
　ＣＡ＝２Ｒ sin(∠Ｂ)

(2)に代入して
１−ε＜ sin(∠Ｂ)
―――――――
sin(∠Ａ)		 ＜ １＋ε　…(3)

ここで、角度の単位をラジアン単位（高校・数III）とします。

△ＡＢＣは近似正三角形なので、
α＝∠Ａ− π
―――
３		 ，β＝∠Ｂ− π
―――
３
とおくと、

α，βは０に近い値となるので、
（←図を書けばせいぜい６度＝0.1ラジアンぐらいと判る）
微分法（三角関数の微分、接線の方程式、高校・数III）より次の１次近似式が得られます。

　sin(∠Ａ)
＝sin( π
―――
３		 ＋α)
≒sin( π
―――
３		 )+α cos( π
―――
３		 )
＝ ＋α
――――――
２		 　…(4)


　sin(∠Ｂ)
＝sin( π
―――
３		 ＋β)
≒sin( π
―――
３		 )+β cos( π
―――
３		 )
＝ ＋β
――――――
２

この三角関数の１次近似式(4)を(3)に代入すると

１−ε＜ ＋β
――――――――
＋α		 ＜１＋ε

−ε＋α−αε＜＋ β
―――
 ＋ε＋α＋αε

ここで、εもαも０に近い値なのでαε≒０として整理すると、

−ε＜β−α＜ε　…(5)

α＝∠Ａ− π
―――
３		 ，β＝∠Ｂ− π
―――
３		 より、

−ε＜∠Ｂ−∠Ａ＜ε…(6)

同様の議論により、近似正三角形ＡＢＣに対して次の２式も得られます。

−ε＜∠Ｃ−∠Ｂ＜ε…(7)

−ε＜∠Ａ−∠Ｃ＜ε…(8)

さらに、この(6)(7)(8)は、（誤差を無視すれば）、
△ＡＢＣが近似正三角形であるための必要十分条件となります。

（Ｓｔｅｐ２）確率

ある定まった円周上に、３点Ａ，Ｂ，Ｃが一様に分布しているとします。

△ＡＢＣに対して，座標空間内に
点Ｑ（∠Ａ，∠Ｂ，∠Ｃ）を取ります。

このとき，点Ｑはｘｙｚ空間内で
「ｘ＋ｙ＋ｚ＝π、ｘ≧０、ｙ≧０、ｚ≧０」を満たす正三角形上に一様に分布しています。

この正三角形は、１辺の長さがπで、
面積は
――――
２		 π2 です。

ここで、先の３条件(6)(7)(8)

−ε＜∠Ｂ−∠Ａ＜ε…(6)

−ε＜∠Ｃ−∠Ｂ＜ε…(7)

−ε＜∠Ａ−∠Ｃ＜ε…(8)

が成り立つような点Ｑ（∠Ａ，∠Ｂ，∠Ｃ）の存在する領域は、正六角形となります。

この正六角形は、１辺の長さがεで、
面積は ３ε2 です。

以上より，△ＡＢＣが近似正三角形である確率は、近似的に

３ε2÷
―――
２		 π2
＝ ６ε2
―――
π2
＝０．００１５２

となることが判ります。

（Ｓｔｅｐ３）　誤差の評価

以上の近時計算で誤差が出てくるのは、(2)(4)(5)の三ヶ所です。
独断と偏見でこの誤差を評価してみましょう。

(2)では、ε2≒０としており、約３パーセントほど結果が小さくなる方向に影響する。

(4)では、テイラー展開（高校では習わない）で
α2≒０とみなしたものである。
不等式の左側と右側では、結果に及ぼす影響が逆なので、意外と影響が少ないであろう。

(5)では、αε≒０としている。
αが正のときと負のときとでは，結果に及ぼす影響が逆である。
影響が小さいといいのだが。

（Ｓｔｅｐ４）　おまけ

(2)式で、εのかわりに
１−η
―――――
１＋η		 ＝０．９５
となる値ηを導入して議論するのも面白い。

このとき、次の式を導くことができる。
（三角比の和積の公式、相互関係、高校・数学II）

−η tan( ∠Ａ＋∠Ｂ
―――――
２		 )＜tan( ∠Ａ−∠Ｂ
―――――
２		 )＜ηtan( ∠Ａ＋∠Ｂ
―――――
２		 )

最も、次の３つの近似式

　２η≒ε、

tan( ∠Ａ＋∠Ｂ
―――――
２		 )≒

tan( ∠Ａ−∠Ｂ
―――――
２		 )≒ ∠Ａ−∠Ｂ
―――――
２

から、(6)式とほぼ同じと言ってもよい。

◆神奈川県　いわし　さんからの解答

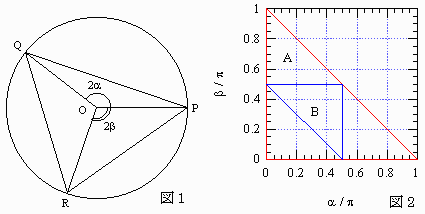
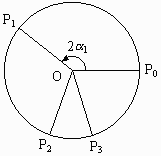
図1のように、中心Oの単位円周上に3点P, Q, Rをとり、

∠POQ=2α、∠POR=2βとおきます。

α, βのとりうる範囲Aは

α≧0, β≧0, α+β≦π (1)

(図2の赤い三角形の周および内部)で、
(α, β)はAに一様に分布すると考えられます。

Aの面積S0は
S0= π2
―――
２		 　(2)です。

△PQRが鈍角三角形のとき、最短辺と最長辺の比
r＜ １
―――
 ＜0.8より

△PQRはT(0.95)とならないので、

α≦π/2,β≦π/2,α+β≧π/2　(3)

の範囲Bを考えれば十分です。
(図2の青い三角形の周および内部)

この範囲で、
PQ=2sinα,　PR=2sinβ, QRの大小は
α, β, π−α−βの大小に一致します。

いま、最長辺をPQ、最短辺をPRとすると、

β≦π−α−β≦αすなわち

β≧π−2α　(4)　かつ
β≦ π−α
――――
２		 　(5)

さらに、△PQRがT(0.95)のとき
r= PR
―――
PQ		 ≧0.95より

sinβ≧0.95sinα (6)

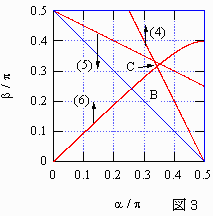
(4),(5),(6)を満たす範囲Cの面積をSとすれば、
△PQRが最長辺をPQ、最短辺をPRとしてT(0.95)となる確率qは

q= S
―――
S0		 　(7) です。

(図3のように、範囲Cは範囲Bに含まれています)

△PQRが、これと異なる最長辺と最短辺の組み合わせで
T(0.95)となる確率もqに等しく、最長辺と最短辺の組み合わせは全部で
3×2=6通りありますから、

△PQRがT(0.95)となる確率pは

p=6q　(8)です。

円周上にn(≧3)個の点があるとき、その中から3点を選んで三角形を作ると、
三角形はN=nC3個あり、
そのいずれもがT(0.95)でない確率は
(1−p)Nですから、
T(0.95)が存在する確率pnは

pn =1−(1−p)N　 (9)

となります。

pを見積もってみます。
図4は範囲C近傍の拡大図です。
図のように、境界の交点K, L, Mをとると、(4),(5),(6)より

K(π/3, π/3),
L(Arccos s, 2 Arcsin s),
M(2 Arcsin t, Arccos t),

s=0.95/2, t=1/(2×0.95)

ですから、

K(Kαπ, Kβπ),
L(Lαπ, Lβπ),
M(Mαπ, Mβπ)とおくと

Kα= Kβ=1/3=0.333…,
Lα=0.342…, Lβ=0.315…,
Mα=0.352…, Mβ=0.323…です。

L, M間の境界を線分LMで近似すれば

S
―――
π2		 

≒(Mα−Kα) (Kβ−Lβ)−| Kα−Lα|| Kβ−Lβ|/2−| Lα−Mα|| Lβ−Mβ|/2−| Mα−Kα|| Mβ−Kβ|/2
=0.000133… より

p= 6S
―――
S0		 ≒0.00160…

となって、N.Cさんの結果に近い値が得られました。

主なpnは次の通りです。

n3591522
pn0.001600.01590.1260.5180.915

私の答案の範囲Cは、N.Cさんの点Qが存在する領域である正六角形の1/6に相当するものだと思います。
なるべく近似をしないで解いてみようと思ったのですが、今度はK, L, Mの座標を求めるところで、電卓を使うことになってしまいました。

◆富山県　N.C　さんからの解答

神奈川県のいわしさんの解答をみて、「６角形」の頂点の座標が厳密に得られたことに驚かされました。

いわしさんの解答を追って、ｎ＝３の場合に私も同じ値に到達できました。
そこで、プログラムを利用して実験しました。

実験結果＞　点の個数 N=3
実験結果＞　実験回数 M=25000000
実験結果＞　割合  39707 ÷ 25000000  =  .00158828
確率の理論値がｐのとき、実験をＭ回繰り返して得られる実験値ｑは、

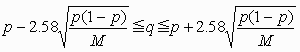
の範囲内にあると考えられます。
（９９％検定）

ここで、ｐ＝0.00160 と仮定すると２５００万回の実験で、実験値ｑは

0.001579377≦ｑ≦0.001620623

を満たすはずですが、
先の実験結果 0.00158828 は問題なくこれを満足しています。
良かった，良かった。

［補足］

ｎ＝１５のときも実験してみました。

実験結果＞　点の個数 N=15
実験結果＞　実験回数 M=1000000
実験結果＞　割合  401736 ÷ 1000000  =  .401736
いわしさんの解答にあるように
理論値をｐ＝0.518 とすると
１００万回の実験で、実験値ｑは

0.516710836≦ｑ≦0.519289164

を満たすはずです。
どこかおかしいですね。

function tantan(a,b,c)
   let tantan=abs(tan((a-b)/2)*tan(c/2))
end function

function chk(A,B,eta)
   let C=pi-A-B
   if tantan(a,b,c)<eta and tantan(b,c,a)<eta and tantan(c,a,b)<eta then 
      LET  chk=1
   else 
      LET  chk=0
   end if
end function

RANDOMIZE

let eta=(1-0.95)/(1+0.95)
let lower=pi/3-3*eta
let upper=pi/3+3*eta
rem △ABCが近似正三角形のとき、lower<∠A<upper が成り立つ。
rem 厳密な評価ではないが、eta<0.15ぐらいまではこれで十分余裕がある。

input PROMPT  "点の個数 N=":N
input PROMPT  "実験回数 M=":M

dim th(n+1) ! I番目の点の位置は、(cos(2*th(i)),sin(2*th(i)))
let th(n+1)=999 ! ループの暴走を防ぐため、非常に大きな数を入れておく。

for MM=1 to M
   let th(n)=pi
   for i=n-1 to 1 step -1   ! 円周上にN個の点を取る。
      let t=pi*rnd
      let j=i
      do while t>th(j+1)   ! 簡略化のためにソートしておく。
         let th(j)=th(j+1)
         let j=j+1
      loop
      let th(j)=t
   next i
    
   let f=0
   let i=1
   let j0=2
   let k0=3
   do while th(i)<upper and f=0 ! ∠C=(th(i)+(pi-th(k)))＜upper である。
      do while th(j0)<th(i)+lower ! ∠A=(th(j)-th(i))＞lower である。
         let j0=j0+1
      loop
      let j=j0
      do while th(j)<th(i)+upper and f=0 ! ∠A=(th(j)-th(i))＜upper である。
         let A=th(j)-th(i)
         do while th(k0)<th(j)+lower
            let k0=k0+1
         loop
         let k=k0
         do while th(k)<th(j)+upper and f=0
            let B=th(K)-th(j)
            let f=chk(A,B,eta)
            let k=k+1
         loop
         let j=j+1
      loop
      let i=i+1
   loop
   if f=1 then let cnt=cnt+1
next mm

print "割合 ";cnt;"÷";M;" = ";cnt/M

END

◆神奈川県　いわし　さんからのコメント

N.Cさんの「近似正三角形」の解答に対して、コメントさせてください。

pnを求めるくだりは私も自信がなかったので、シミュレーションで確かめるつもりでした。
どうもありがとうございました。

合わない理由を考えてみると、円周上の各点から作った三角形の形がお互いに独立ではないために、
すべてがT(0.95)でない確率を(1-p)Nとしてはいけない、ということのような気がします。

もう少しよく考えてみます。

◆神奈川県　いわし　さんからのコメント

n=4の場合を考えてみます。

　

図のように、中心Oの単位円周上に
4点P0, …, P3をこの順に反時計回りにとり、
OP0から反時計回りに測った∠P0OPk (k=1, 2, 3) を
2αkとおきます。

さらに
x= α1
―――
π		 , y= α2
―――
π		 , z= α3
―――
π		 とおくと、

Q(x, y, z) のとり得る範囲は0≦x≦y≦z≦1です。
(図の赤い三角錐の内部)

　

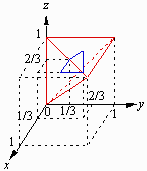
その中で、△PaPbPc (0≦a＜b＜c≦3) の中に正三角形が存在するのは、Qが図のような、三角錐の面上の点をつないだ青いリング状の線上にあるときであり、
T(0.95)が存在するのは、Qが、青い線の周りに六角形に広がった、ちょうど鉛筆を4本つないで輪を作ったような立体Vの内部にあるときです。

Vの体積を求めて、赤い三角錐の体積で割ればp4が求まるわけですが…。

　

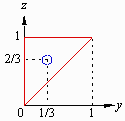
yz面上では、概ね図のようになっていて、青い部分と赤い部分の面積比は
p=0.00160…ですが、リングの頂点で鉛筆同士が重なるため、Vの体積は単純なpの関数では書けません。(と思う)

近似的に解く手段はあるかもしれませんが、それは私の能力を超えています。
まして、(n−1) 次元空間内のnC3本の鉛筆となると…。
というわけで、問題を甘く見ていました。

　『近似正三角形』へ

　数学の部屋へもどる