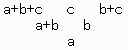
◆東京都 goya さんからの解答。
【問題1】
(1) 5 2 6
3 4
1
(2) 4 1 6
3 5
2
(3) 5 6 2
1 4
3
(4) 4 6 1
2 5
3
正解は上の4つ(左右反転したものを含めると8つ)だと思います。
問題2以降は何となく解無しのような気がします。
【コメント】
問題2以降は私も自信がありません。
解はあるような気がするのですが、どうでしょうか?
わかった方、教えてください。
◆広島県 清川 育男 さんからの解答。
プログラムを組んでコンピュータに解かせました。
【問題1】
GOYAさんの解答に同じです。
【問題2】
解なし。
【問題3】
13 3 15 14 6 6 14 15 3 13
10 12 1 8 8 1 12 10
2 11 7 7 11 2
9 4 4 9
5 5
【問題4】
もし解が存在するとすれば、最上段に21があるはずです。
A B C D E F
かつA,B,Cのなかに21がある解があるはずです。
しかしそのなかに解がないのでこの問題の解はなし。
Basicはインタプリタ型なのでBreakして途中の変数の値を見れるのがいいですね。
スピードは遅いが。
【コメント】
残念ながら、問題2はやはり解なしのようです。
問題3になると、解がでてくるのが面白いですね。
問題3はコンピュータなしで解けないものでしょうか?
◆新潟県 ぽぽぽ さんからの解答。
問2に関してです。
ただ適当に当てはめてたら解が見つかってしまいました。
なんとなく見つけたので、他にも解があるのかどうか検証してませんが、とりあえず解なしではないようです。
6 10 1 8
4 9 7
5 2
3
【コメント】
なんと問題2に解が見つかってしまいました。
教えていただいてどうもありがとうございます。
ひょとして他にもあるのでしょうか。
楽しみです。
◆広島県 清川 育男 さんからの解答。
【問題2】
間違っていました。
6 1 10 8 6 10 1 8
5 9 2 4 9 7
4 7 5 2
3 3
以上4通りあります。(左右対称を許せば8通り)
8 3 10 9 8 10 3 9
5 7 1 2 7 6
2 6 5 1
4 4
言い訳になりますがある予測があって手抜きをしていました。
◆兵庫県 ken8 さんからの解答。
【問題1】
6 1 4
5 3
2
【問題2】
8 10 1 6
2 9 5
7 4
3
最大数が最上段にくることは間違いない
(ほかの数で引きようがない)
問題1と2においては最下段に入る数字は(段数−1)で辺に沿って1ずつ増やした数を入れて後は足し算で下から埋めていきました。
何の根拠もありません。
◆岐阜県の中学校3年生 さちえ さんからの解答。
【問題1】
6 2 5
4 3
1
◆神奈川県 ココット さんからの解答。
【問題4】
存在しません。
(20段まではパソコンで確認しました)
6段以上では存在しないのですが、証明は苦労しました。
全部書くのは大変なので、途中まで書きます。
(1)各行で最大の数をつないだ「ライン」が存在する。
N段の数入れパズルを考える。
一番上の段以外のある数(Aと置く)に注目したとき、その上の2つの数のうちどちらかはAより大きくなる。
つまり、一番下の段から見ると、1段ごとに数が足されて大きくなっていく。
同じ数を使わないで、最上段までもっとも小さくなるようにする場合、
N−1段足していく間に、1からN−1までを1つずつ使うことになる。
その和は
B+N(N−1)/2
となる。
Bを、足し算に使わなかった最小値であるNとすると、上記の和は
N(N+1)/2
となる。
これはN段の数入れパズルで使うことができる最大の数である。
(つまり、下から順に最小になるように足しても、最上段では最大値を使わなければならなくなる)
よって、最下段から最上段までに必ず1からNまでの数が使われ、かつ各段での最大値をつなぐ(ぎざぎざの)「ライン」が存在する。
また、「ライン」上の値のどちらかの隣には1からNのどれかが1つだけ存在する。
(2)証明
最終的には「根性で解く」ような形になるのですが、そのための説明です。
N段の数入れパズルで、1からNまでの値をa,b,c…とおく。
最下段から順に、a,b,c…と入れていく。
このとき、最大のラインが左に行くような形から順に考えていく。
例えば3段の場合で「ライン」が左に寄るようにすると、以下のようになる。
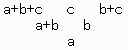
a,b,c…以外の値はNより大きく、「ライン」の値よりも小さくなければならない。
これにより、3段目(最上段)の右上は c-b とはならずに b+c となる。
また、この時点でa,b,cには1から3までのどの数が入るかはわからないが、
(1)よりb+cは3(=N)より大きくなる。
そして、この時点では(a,b,c)=(1,3,2)または(2,3,1)とすることで3段の解答が得られる。
同様に、5段で「ライン」が左に寄るようにすると、以下のようになる。
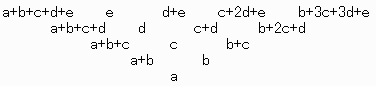
下から4段目の一番右は
b+2c+d ( =(b+c)+(c+d) )となっているが、これは引き算にしてしまうと
(c+d)-(b+c) = -b+d < N
となってしまい、(1)の性質を満たさなくなってしまうためである。
最上段の右から2番目も同様である。
さて、ここで最上段の一番右(b+3c+3d+e)に注目する。
ここも引き算にしてしまうと
(c+2d+e)-(b+2c+d) = (d+e)-(b+c)
ここで
d+e<2N … d,e<Nより
b+c > N … (1)より
であるので、
(d+e)-(b+c) < N
となってしまい、(1)の性質を満たさなくなる。
また、
b+3c+3d+e = 2(c+d)+b+c+d+e>a+b+c+d+e
となってしまうので、足し算にしてもうまくいかない。
よって、この形での5段は、a,b,c,d,eに(1)を満たすどのような数を入れても構成不可能である。
他のパターンについても考え方は同様であるが、手間がかかるのでここでは省略する。
◆神奈川県 ココット さんからのコメント。
このパズルで、6段以上は作成不可能である証明はないと思っていたのですが、20年以上も前に証明されていたことがわかりました。
マーチン・ガードナーの「数学ゲーム」発行が1977年なので、すぐに解けたということなのでしょうか…。
証明が載っている文献は
BULLETIN OF THE INSTITUTE OF MATHEMATICS ACADEMIA SINICA Volume 5, Number 1, June 1977 p191-197 タイトル:EXACT DIFFERENCE TRIANGLES 著者:G.J.CHANG, M.C.HU, K.W.LIH, A.C.SHIEHです。
幸い、言語が英語だったので、私のつたない英語力でもなんとか読むことができました。
証明のあらすじとしては、一般にn行(段)の三角形を考えたとき、1〜nまでの数字が各行で1度ずつ現れる。
各行で最大値の上限が存在する。
大きい方からn+1個までの数をbとすると、
bは、下からn-2行までは1個しか存在できない。
bは、上から2行目では2個までしか存在できない。
bは、最上段では (n+5)/3 個までしか存在できない。
u= n(n-1)/2-1 とすると、
uまたはb は、下からn-2行までは1個しか存在できない。
bが上から2行目で2個存在する場合、uは、上から2行目には存在しない。
uが最上段にある場合、bとは2つ以上離れている必要がある。
これらの条件から、証明をしていました。
しらみつぶしの検索などは使わず、スマートに解かれています。
◆東京都 kyopapa oyaji さんからの解答。
【問題2】
| 8 | 10 | 3 | 9 | |||
| 2 | 7 | 6 | ||||
| 5 | 1 | |||||
| 4 |