A=3k+1のとき,
(3k+1)nを展開した項のうち,kの2次以上の項は,3を因数として2個以上もつから、9の倍数となる。
kの1次以下 3nk+1 を考えればよい。
nが6の倍数のとき,n=6m(mは整数)と表せる。
3nk+1=18mk+1 となり,Aを9で割った余りは 1。
A=3k−1のときも,同様にして,
−18mk+1 となり,Aを9で割った余りは 1。
【問題3】
剰余系の乗法の規則より,問題2の結果から,明らか。
P.S.
Aが,2と5,4と7で逆並びになるのに対し,A=1,8の相棒が無いのが何故か気にいらない。
美しさに欠けると思いますが・・・。
◆東京都 鳳 奥人 さんからの解答。
【問題1】
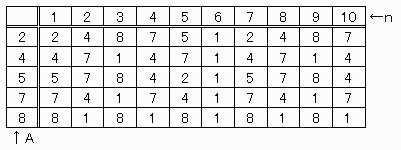
【問題2】
まず、6乗の時は・・・
Aを3s+k(sは0以上の整数で、kは1または2)とすると
(3s+k)6 =1*(3s)6*k0+6*(3s)5*k1+15*(3s)4*k2+20*(3s)3*k3+15*(3s)2*k4+6*(3s)*k5+k6これをkについての6次式と考える。
k0〜k4までの項はいずれも係数に含まれる3sの累乗がすでに9で割りきれる。
k5の項も、係数の6*3s が9で割りきれる。
というわけで、問題はk6の項。
9で割りきれないことは明白。
では、9で割った時の余りは
k=1のとき 考えるまでもなく1
k=2のとき 2の6乗は64だから1
とりあえず、n=6のときはこんな具合です。
そうすると、nが6の倍数だったときは、同様にkについてのn次式を考えると、
k0〜kn-2までの項はいずれも係数に含まれる3sの累乗が9で割りきれる。
kn-1の項は、
係数の3s*nC2=3s*n(n-1)が9で割りきれる。
(nは当然3の倍数でもあるから)
残るはknの項。
nが6の倍数ということは、knはk6の累乗。
k=1のときは、やはり考えるまでもなく9で割った余りは1。
k=2のとき、
kn = (k6)n/6 =64n/6=(63+1)n/6
ここでt = n/6 とすると、kn = (63+1)t
計算はしませんが、このまま展開すれば1tの「項」だけが9で割りきれず、割った余りが1になることは明白です。
結論:nが6の倍数のときはMは必ず1になる!
【問題3】
A=9a+b(aは0以上の整数、bは1以上8以下の整数)とおく。
また、問題2より、(9a+b)6n を9で割った余りは1になるから、
(9a+b)6n = 9c+1(cは0以上の整数)とおく。
すると
A6n+1
=(9a+b)6n+1
=(9a+b)(9a+b)6n
=(9a+b)(9c+1)
=9(9ac+a+bc)+b
これを9で割った余りはb。
つまり、Aを9で割った余りと等しい。