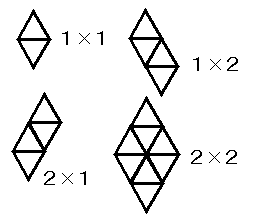
◆静岡県 ヨッシーさんからの解答。
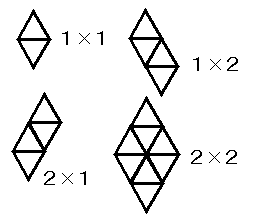
図のように、60度の角が上下方向に向いているものを数え、3倍します。
上の頂点から、左下、右下に伸びている辺の長さで、m×nのように表します。
1辺tの正三角形では、t≧m+nの平行四辺形が出来ます。
【問題1】1辺が3
1×1・・・3×(1+2)=9個
1×2・・・3×1 =3個
2×1・・・3×1 =3個 計15個
【問題2】1辺が4
1×1・・・3×(1+2+3)=18個
1×2・・・3×(1+2) = 9個
1×3・・・3×1 = 3個
2×1・・・3×(1+2) = 9個
2×2・・・3×1 = 3個
3×1・・・3×1 = 3個 計45個
【問題3】1辺が5
1×1・・・3×(1+2+3+4)=30個
1×2・・・3×(1+2+3) =18個
1×3・・・3×(1+2) = 9個
1×4・・・3×1 = 3個
2×1・・・3×(1+2+3) =18個
2×2・・・3×(1+2) = 9個
2×3・・・3×1 = 3個
3×1・・・3×(1+2) = 9個
3×2・・・3×1 = 3個
4×1・・・3×1 = 3個 計105個
【問題4】1辺がN
1辺がkのときとk+1の時を比較すると、
3×{1+(1+2)+(1+2+3)+・・+(1+2+3+・・+k)}個増えます。
つまり、1辺がkの時の平行四辺形の個数をSkとすると、
Sk+1−Sk
| =3× | k Σ m=1 | { | m Σ n=1 | n} |
| =3× | k Σ m=1 | m(m+1) ――――― 2 |
| = | k(k+1)(k+2) ――――――――― 2 |
S1=0より、
SN
| =S1+ | N-1 Σ m=1 | m(m+1)(m+2) ―――――――― 2 |
| = | (N−1)N(N+1)(N+2) ――――――――――――― 8 |
| 計 | (N−1)N(N+1)(N+2) ――――――――――――― 8 | 個 |
【コメント】
この問題はそうとう難問かと思ったのですが、すばらしいです。
実は解答がこないのではないかとあきらめていました。
かなり美しい解だと思うのですが、どうでしょう。
◆広島県 清川 育男さんからのコメント。
実にスマートな解答で見惚れていましたが、そのうち以前、見た式に似ていることにきずきました。
「正三角形の個数」の問題です。
「正三角形の個数」のときはNは石の個数で、「平行四辺形の個数」のときはNは辺の個数ですから、(+1の関係にあります。)単純に比較は出来ないですね。
しかし、分子がピッタリ一致していたものですから驚きました。
平行四辺形の個数をB(n)、正三角形の個数をA(n)とするとき、
B(n)=3×A(n-1),n≧2,A(1)=1
やはり何か関係がありそうです。
出題の意図もこのことを踏まえておられるのでしょうね。
【コメント】
もちろん、それを考えての出題です・・・。といいたいのですが、最初に答えが一致することを見つけたのは単なる偶然です。
別々に考えていた問題の解が一致して、私も驚きました。
一応、両方ともオリジナルの問題なのですが、どこにでもありそうな問題ですから類題もあるかもしれません。
だれか関係を明解に示してくれないかなぁ。