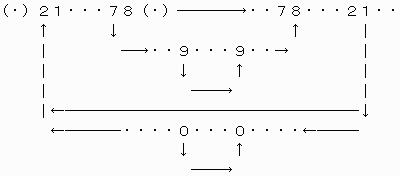
◆東京都 You.O さん からの解答。
条件を満たす整数が前に述べたもの以外に存在しないことを示しておきたいと思います。
数式と整数条件で数学っぽく解いてもよいのですが、小学生っぽく筆算(覆面算)で解いてみたいと思います。
ただし下のように通常とは少し異なった規則で覆面算を行います。
1.それぞれの文字は0以上9以下の数字を表す。
2.整数の最上位にある文字は1以上9以下の文字を表す。
※3.Pは2以上9以下のある数字を表す。
4.同一の文字は同一の数字を表す。
※5.相異なる文字が表す数字は異なるとは限らない。
力わざではありますが、力わざというほど労力を要するものでもないと思います。
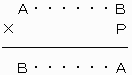
[0]条件を満たす整数の上1ケタと下1ケタについて次のような覆面算を考える。

P=2のときA×P<10,1≦A≦9よりA=1,2,3,4のいずれかである。
ただし、B×2の一の位がAであることから、A=2または4となる。
A=2とすると、B×2の一の位が2であるからB=1または6。
一方、最上位についてA×P≦B<(A+1)×P
すなわち4≦B<6であるから、B=4または5。
よって、Bにあてはまる適当な数字が存在しない。
すなわち、P=2,A=2の場合はあり得ないことになる。
同様にして、A=4の場合も考えられないことがわかる。
P=3のときA=1,2,3のいずれかである。
ところが、上と同様にして、A=1,2,3のいずれの場合も考えられないことがわかる。
P=4のときA=1,2のいずれかであるが、B×4の1の位がAであることから、A=2となる。
このとき、B×4の一の位が2であるからB=3または8。
一方、最上位について8≦B<12かつ1≦B≦9であるから、B=8または9。
よって、P=4,A=2,B=8のとき条件を満たす。
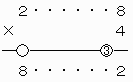
なお、上で○をつけた繰り上がりの数が0と3で異なるので、これらが重なるように上2ケタを移動させて、下のような計算を成り立たせることはできない。
28×4=82
したがって、このような形の2ケタの整数で条件を満たすものは存在しないことがわかる。
また、上から2ケタ目および下から2ケタ目の数字の決め方は後述[2]の通りである。
P=5,6,7,8,9のときA=1となるが、このうちBにあてはまる適当な数字が存在するのはP=9のときで、このときB=9となる。
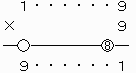
なお、上で○をつけた繰り上がりの数が0と8で異なるので、これらが重なるように上2ケタを移動させて、下のような計算を成り立たせることはできない。
19×9=91
したがって、このような形の2ケタの整数で条件を満たすものは存在しないことがわかる。
一方、いずれの場合についてもA≠Bであるため、1ケタの整数で条件を満たすものは存在しないことがわかる。
また、上から2ケタ目および下から2ケタ目の数字の決め方は後述[1]の通りである。
[1]A=1,B=9,P=9のとき
次のような覆面算を考えることになる。
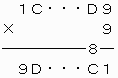
(10+C)×9<100でなければならないから、C=0または1となる。
(ア)C=0の場合
十の位について、9×D+8の一の位が0であるから、9×Dの一の位は2となる。
よって、D=8となる。
なお、C≠Dであるため、このような形の3ケタの整数で条件を満たすものは存在しないことがわかる。
このとき、上から2ケタ目について、1つ下の位からの繰り上がりの数が8でなければならない。
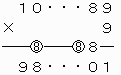
上で○をつけた繰り上がりの数がいずれも8なので、これらが重なるように上2ケタを移動させて、下のような計算を成り立たせることができる。
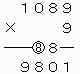
したがって、4ケタの整数1089は条件を満たすことがわかる。
また、上から3ケタ目および下から3ケタ目の数字の決め方は後述[3]の通りである。
(イ)C=1の場合
十の位について、9×D+8の一の位が1であるから、9×Dの一の位は3となる。
よって、D=7となる。ところが上2ケタについて、
90+D≧11×9
が成り立たなければならないから、0≦D≦9よりD=9。
ゆえに、Dにあてはまる適当な数字が存在しない。
すなわち、C=1の場合はあり得ないことがわかる。
[2]A=2,B=8,P=4のとき
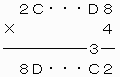
(20+C)×4<90でなければならないから、C=0,1,2のいずれかとなる。
ところが、十の位について、4×D+3の一の位がCであるから、C=1となる。
このとき、4×Dの一の位が8であるから、D=2または7。
一方、上2ケタについて、
21×4≦80+D<22×4
が成り立たなければならないから、4≦D<8。
ゆえに、D=7となる。
なお、C≠Dであるため、このような形の3ケタの整数で条件を満たすものは存在しないことがわかる。
このとき、上から2ケタ目について、1つ下の位からの繰り上がりの数が3でなければならない。
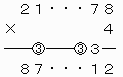
上で○をつけた繰り上がりの数がいずれも3なので、これらが重なるように上2ケタを移動させて、下のような計算を成り立たせることができる。
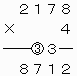
したがって、4ケタの整数2178は条件を満たすことがわかる。
また、上から3ケタ目および下から3ケタ目の数字の決め方は後述[4]の通りである。
[3]A=1,B=9,C=0,D=8,P=9のとき
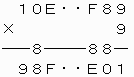
上から3ケタ目について、1つ上の位への繰り上がりの数が8であるので、
(E+1)×9>80
でなければならない。
よって、E=8または9。
(ア)E=8の場合
百の位について、9×F+8の一の位が8であるから、9×Fの一の位は0となる。
よって、F=0となる。
なお、E≠Fであるため、このような形の5ケタの整数で条件を満たすものは存在しないことがわかる。
このとき、上から3ケタ目について、1つ下の位からの繰り上がりの数が
(80+F)−E×9=8
でなければならない。
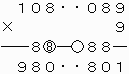
上で○をつけた繰り上がりの数が8と0で異なるので、これらが重なるように上2ケタを移動させて、下のような計算を成り立たせることはできない。
108089×9=980801
したがって、このような形の6ケタの整数で条件を満たすものは存在しないことがわかる。
また、上から4ケタ目および下から4ケタ目の数字の決め方は後述[5]の通りである。
(イ)E=9の場合
百の位について、9×F+8の一の位が9であるから、9×Fの一の位は1となる。
よって、F=9となる。
このとき、上から3ケタ目について、1つ下の位からの繰り上がりの数が
(80+F)−E×9=8
でなければならない。
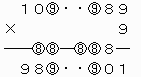
なお、上で○をつけた数どうしが重なるように上2ケタを移動させて、下のような計算を成り立たせることができる。
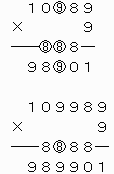
したがって、5ケタの整数10989および6ケタの整数109989は条件を満たすことがわかる。
また、上から4ケタ目および下から4ケタ目の数字の決め方は後述[6]の通りである。
[4]A=2,B=8,C=1,D=7,P=4のとき
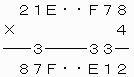
上から3ケタ目について、1つ上の位への繰り上がりの数が3であるので、
(E+1)×4>30
でなければならない。
よって、E=7,8,9のいずれかとなる。
ところが、百の位について、4×F+3の一の位がEであるから、E=7または9。
(ア)E=7の場合
百の位について、4×F+3の一の位が7であるから、4×Fの一の位は4となる。
よって、F=1または6。一方、上3ケタについて、
217×4≦870+F<218×4
が成り立たなければならないから、0≦F<2。
ゆえにF=1となる。
なお、E≠Fであるため、このような形の5ケタの整数で条件を満たすものは存在しないことがわかる。
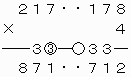
上で○をつけた繰り上がりの数が3と0で異なるので、これらが重なるように上2ケタを移動させて、下のような計算を成り立たせることはできない。
217178×4=871712
したがって、このような形の6ケタの整数で条件を満たすものは存在しないことがわかる。
また、上から4ケタ目および下から4ケタ目の数字の決め方は後述[7]の通りである。
(イ)E=9の場合
百の位について、4×F+3の一の位が9であるから、4×Fの一の位は6となる。
よって、F=4または9。一方、上3ケタについて、
219×4≦870+F<220×4
が成り立たなければならないから、6≦F≦9。
ゆえにF=9となる。
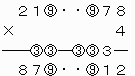
なお、上で○をつけた数どうしが重なるように上2ケタを移動させて、下のような計算を成り立たせることができる。
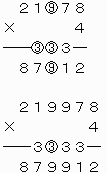
したがって、5ケタの整数21978および6ケタの整数219978は条件を満たすことがわかる。
また、上から4ケタ目および下から4ケタ目の数字の決め方は後述[8]の通りである。
[5]A=1,B=9,C=0,D=8,E=8,F=0,P=9のとき
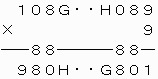
上から4ケタ目について、1つ上の位への繰り上がりの数が8であるので、
(G+1)×9>80
でなければならない。
よって、G=8または9。
(ア)G=8の場合
千の位について、9×Hの一の位が8であるから、H=2となる。
このとき、上から4ケタ目について、1つ下の位からの繰り上がりの数が
(80+H)−G×9=10
でなければならないが、繰り上がりの数は9以下であるので、このようなことはあり得ない。
したがって、このような形の整数で条件を満たすものは存在しないことがわかる。
(イ)G=9の場合
千の位について、9×Hの一の位が9であるから、H=1となる。
なお、G≠Hであるため、このような形の7ケタの整数で条件を満たすものは存在しないことがわかる。
このとき、上から4ケタ目について、1つ下の位からの繰り上がりの数が
(80+H)−G×9=0
でなければならない。
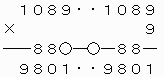
上で○をつけた繰り上がりの数がいずれも0なので、これらが重なるように上2ケタを移動させて、下のような計算を成り立たせることができる。
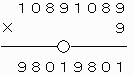
したがって、8ケタの整数10891089は条件を満たすことがわかる。
また、上から5ケタ目および下から5ケタ目の数字の決め方は後述[9]の通りである。
[6]A=1,B=9,C=0,D=8,E=9,F=9,P=9のとき
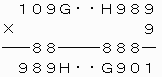
上から4ケタ目について、1つ上の位への繰り上がりの数が8であるので、
(G+1)×9>80
でなければならない。
よって、G=8または9。
(ア)G=8の場合
千の位について、9×H+8の一の位が8であるから、9×Hの一の位は0となる。
よって、H=0。
なお、G≠Hであるため、このような形の7ケタの整数で条件を満たすものは存在しないことがわかる。
このとき、上から4ケタ目について、1つ下の位からの繰り上がりの数が
(80+H)−G×9=8
でなければならない。
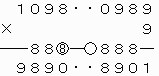
上で○をつけた繰り上がりの数が8と0で異なるので、このような形の8ケタの整数で条件を満たすものは存在しないことがわかる。
また、上から5ケタ目および下から5ケタ目の数字の決め方は[5]と同様になる。
(イ)G=9の場合
千の位について、9×H+8の一の位が9であるから、9×Hの一の位は1となる。
よって、H=9。
このとき、上から4ケタ目について、1つ下の位からの繰り上がりの数が
(80+H)−G×9=8
でなければならない。
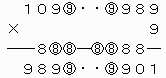
なお、上の計算式を見てわかるように、7ケタの整数1099989および8ケタの整数10999989は条件を満たす。
また、上から5ケタ目および下から5ケタ目の数字の決め方は[6]と同様になる。
[7]A=2,B=8,C=1,D=7,E=7,F=1,P=4のとき
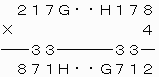
上から4ケタ目について、1つ上の位への繰り上がりの数が3であるので、
(G+1)×4>30
でなければならない。
よって、G=7,8,9のいずれかとなる。
ところが、千の位について、4×Hの一の位がGであるから、G=8。
千の位について、4×Hの一の位が8であるから、H=2または7となる。
一方、上4ケタについて、
2178×4≦8710+H<2179×4
が成り立たなければならないから、2≦H<6。
ゆえにH=2となる。
なお、G≠Hであるため、このような形の7ケタの整数で条件を満たすものは存在しないことがわかる。
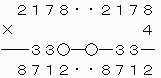
上で○をつけた繰り上がりの数がいずれも0なので、これらが重なるように上2ケタを移動させて、下のような計算を成り立たせることができる。
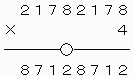
したがって、8ケタの整数21782178は条件を満たすことがわかる。
また、上から5ケタ目および下から5ケタ目の数字の決め方は後述[10]の通りである。
[8]A=2,B=8,C=1,D=7,E=9,F=9,P=4のとき
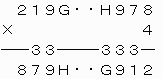
上から4ケタ目について、1つ上の位への繰り上がりの数が3であるので、
(G+1)×4>30
でなければならない。
よって、G=7,8,9のいずれかとなる。
ところが、千の位について、4×H+3の一の位がGであるから、G=7または9。
(ア)G=7の場合
千の位について、4×H+3の一の位が7であるから、4×Hの一の位は4となる。
よって、H=1または6。
一方、上4ケタについて、
2197×4≦8790+H<2198×4
が成り立たなければならないから、0≦H<2。
ゆえにH=1となる。
なお、G≠Hであるため、このような形の7ケタの整数で条件を満たすものは存在しないことがわかる。
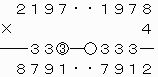
上で○をつけた繰り上がりの数が3と0で異なるので、このような形の8ケタの整数で条件を満たすものは存在しないことがわかる。
また、上から5ケタ目および下から5ケタ目の数字の決め方は[7]と同様になる。
(イ)G=9の場合
千の位について、4×H+3の一の位が9であるから、4×Hの一の位は6となる。
よって、H=4または9。
一方、上4ケタについて、
2199×4≦8790+H<2200×4
が成り立たなければならないから、6≦H≦9。
ゆえにH=9となる。
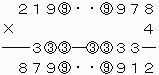
なお、上の計算式を見てわかるように、7ケタの整数2199978および8ケタの整数21999978は条件を満たす。
また、上から5ケタ目および下から5ケタ目の数字の決め方は[8]と同様になる。
[9]A=1,B=9,C=0,D=8,E=8,F=0,G=9,H=1,P=9のとき
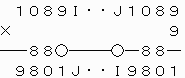
上で○をつけた繰り上がりの数がいずれも0なので、次のような覆面算に還元できる。
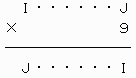
(ア)I≠0の場合
この解答の冒頭で述べた[0]でA→I,B→J,P=9とした場合に相当する。
したがって、I=1,J=9。
なお、I≠Jであるため、このような形の9ケタの整数で条件を満たすものは存在しないことがわかる。
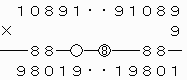
上で○をつけた繰り上がりの数が0と8で異なるので、このような形の10ケタの整数で条件を満たすものは存在しないことがわかる。
また、上から6ケタ目および下から6ケタ目の数字の決め方は[1]と同様になる。
(イ)I=0の場合
一万の位について、9×Jの一の位が0であるから、J=0となる。
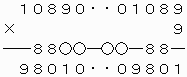
なお、上の計算式を見てわかるように、9ケタの整数108901089および10ケタの整数1089001089は条件を満たす。
また、上から6ケタ目および下から6ケタ目の数字の決め方は[9]と同様になる。
[10]A=2,B=8,C=1,D=7,E=7,F=1,G=8,H=2,P=4のとき
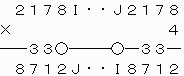
上で○をつけた繰り上がりの数がいずれも0なので、次のような覆面算に還元できる。
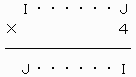
(ア)I≠0の場合
この解答の冒頭で述べた[0]でA→I,B→J,P=4とした場合に相当する。
したがって、I=2,J=8。
なお、I≠Jであるため、このような形の9ケタの整数で条件を満たすものは存在しないことがわかる。
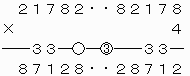
上で○をつけた繰り上がりの数が0と3で異なるので、このような形の10ケタの整数で条件を満たすものは存在しないことがわかる。
また、上から6ケタ目および下から6ケタ目の数字の決め方は[2]と同様になる。
(イ)I=0の場合
一万の位について、4×Jの一の位が0であるから、J=0または5。
ところが上5ケタについて、
21780×4≦87120+J<21781×4
が成り立たなければならないから、0≦J<4。
ゆえにJ=0となる。
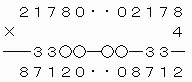
なお、上の計算式を見てわかるように、9ケタの整数217802178および10ケタの整数2178002178は条件を満たす。
また、上から6ケタ目および下から6ケタ目の数字の決め方は[10]と同様になる。
以上により、前にも述べたように次のことが証明された。
上2ケタが"10"、下2ケタが"89"でこれらの間のmケタがすべて"9"であるような数字の並びを《Am》、
上2ケタが"21"、下2ケタが"78"でこれらの間のnケタがすべて"9"であるような数字の並びを《Bn》、
"0"がkケタ連続した数字の並びを《Ok》とし、これらを整数の構成単位の1種と考える。
このとき、9倍すると数字の並びが逆になる数は、
いくつかの構成単位《Am》と《Ok》からなり、
それらの構成単位の順序を逆にしてももとの順序と変わらないものに限られ、
4倍すると数字の並びが逆になる数は、
いくつかの構成単位《Bn》と《Ok》からなり、
それらの構成単位の順序を逆にしてももとの順序と変わらないものに限られる。
なぜなら、例えばP=9の場合、最上位と最下位から順にそれぞれ下位、上位のケタへと数字を決めてゆくことにすると、その決め方には次のような順序があることがわかる
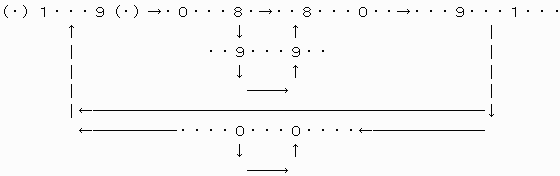
これを単純化すると、次のようになる。
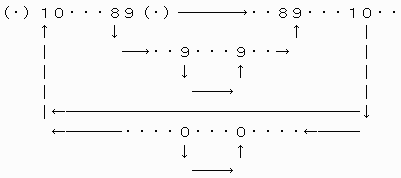
上図の上半分および下の部分がそれぞれ、最上位部と最下位部に
同じ数字の並び《Am》および《Ok》を挿入することを表している。
P=4の場合についても同様で、下図の上半分および下の部分がそれぞれ、最上位部と最下位部に
同じ数字の並び《Bn》および《Ok》を挿入することを表している。