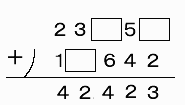
◆広島県 清川 育男 さんからの解答。
【問題2】
7進法表記の問題とする。
23451
+)15642
─────────
42423
【コメント】
いじわるで十進法ではないということを書かなかったのですが、よく見破れましたね。
もちろん正解です。
◆広島県 清川 育男 さんからの解答。
【問題1】
3つの頂点に入った数の和をZとする。
4段目のマスの左からA,B,C,Dとする。
(3Z-(A+3B+3C+D))
((A+2B+C)-Z)) ((B+2C+D)-Z))
(Z-(A+B)) (Z-(B+C)) (Z-(C+D))
A B C D
となる。
10個のマスの和は、4Z−(B+C)=45。
Z=1/4(45+(B+C))
イ)Zが自然数であるためには、1≦B+C≦17のとき
1)B+C=3。 Z=12。
2)B+C=7。 Z=13。
3)B+C=11。Z=14。
4)B+C=15。Z=15。
ロ)イ)の関係から0を入れる事の出来るマスは、BかCである。
ハ)イ)、ロ)の関係から、B+C=7。Z=13。この場合しかない。詳細は省略。
ニ)イ)、ロ)、ハ)から求める答えは左右対称に2通りの場合がある。
その1) その2)
8 8
3 2 2 3
4 6 5 5 6 4
9 0 7 1 1 7 0 9
◆京都府 the king of water gate さんからの解答。
【問題1】
上から順に
(A),(B,C),(D,E,F),(G,H,I,J)とする。
| A | ||||||
| B | C | |||||
| D | E | F | ||||
| G | H | I | J |
三つの頂点の数の和をSとする。
(A+B+C)+(D+G+H)+(F+I+J)+E=45
E=45−3S
よってEは3の倍数である。
E=0,3,6,9
条件に合う入れ方は、
x→(9−x)によって条件に合う入れ方に移るので、
E=6,9はE=0,3の場合からできるのでE=0,3とする。
A+G+J
=(S−B−C)+(S−D−H)+(S−F−I)
=(S−B−D)+(S−C−F)+(S−H−I)
=3E
E=0とするとA,G,Jに入れられないのでE=3となる。
S=(45−3)/3=14
B+D=C+F=H+I=14−3=11
足して11になる組合せは
(2,9),(4,7),(5,6)なので、A,G,Jは0,1,8である。
一つの解の向きを変えたものも解なので、
解はA=0,G=1,J=8の場合からできる。
B+C=14−0=14からB,Cは5,9であり、
F+I=14−8=6からF,Iは2,4であり、
C+F=11なので、
B=5,C=9,F=2,I=4となる。
D=11−5=6
H=11−4=7
よって解は
|
|
◆神奈川県 諏訪 冬葉 さんからの解答。
【問題2】
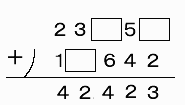
【解答】
| 23451 |
| +15642 |
| 42423 |
一応解答手順
下一桁は□+2=3から1(繰り上がりなし)
二桁目で5+4=12より、5+4−2=7進数と判断
あとは自動的に決まる。